第二章 习题汇总
Q1. 在3台不同指令系统的计算机上运行同一程序P时,A机需要执行
1.0
×
1
0
8
1.0×10^8
1.0×108条指令,B机需要执行
2.0
×
1
0
8
2.0 ×10^8
2.0×108条指令,C机需要执行
4.0
×
1
0
8
4.0×10^8
4.0×108条指令,但实际执行时间都是10s。请分别计算这3台机器在运行程序P时的实际速度,以MIPS为单位。这3台计算机在运行程序P时,哪一台性能最高?为什么?
A1:
MIPS: million instruction per second,表示每秒多少百万条指令,如 10MIPS ,表示每秒一千万条指令。这是衡量CPU速度的一个指标。
公式: M I P S = ( 指令数 / 执行时间 ) / 1 0 6 = 指令数 / ( 执行时间 ∗ 1 0 6 ) ,执行时间的单位是 s MIPS=(指令数/执行时间)/10 ^6 =指令数/(执行时间∗10 ^6),执行时间的单位是 s MIPS=(指令数/执行时间)/106=指令数/(执行时间∗106),执行时间的单位是s
根据这个公式,我们可以计算出A、B、C三台机器的MIPS分别为10, 20, 40。
在运行程序P时,三台计算机的运行时间相同,所以性能相同。【题目问的是运行程序 P 时的性能。】
补充:

Q2: 
A2:
处理器运行程序的性能提升幅度可以用Amdahl定律来计算,公式为:性能提升 = 1 / [(1-P) + P/S]。其中,P是可向量化的百分比,S是向量部件的加速比。
(1) 加速比y和向量化比例x之间的关系是:
y
=
1
(
1
−
x
)
+
x
8
=
1
1
−
7
8
x
y=\frac{1}{(1-x)+\frac{x}{8}}=\frac{1}{1-\frac{7}{8}x}
y=(1−x)+8x1=1−87x1 (A)
图像如下图所示: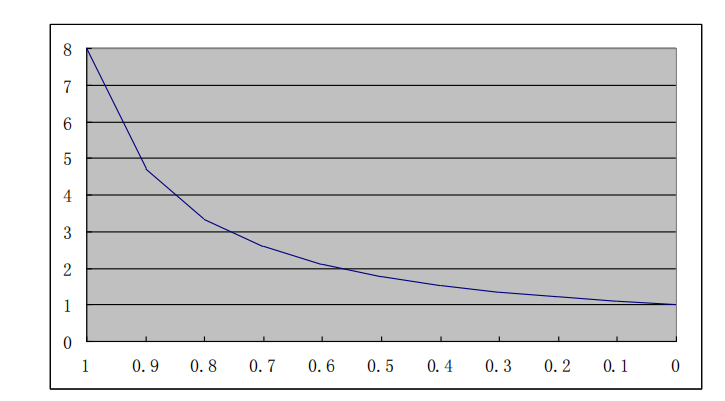
(2) 在式(A)中令 y=2,可解得 x=4/7≈57.14%。
此时向量模式运行时间占总时间比例是 ((4/7)/8)/(3/7+((4/7)/8))=1/7=14.29%
(3)
- 硬件方法:向量部件速度提高一倍,也就是运算速度在8的基础上✖2,但是向量化的百分比不变。
- 软件方法:向量化的百分比增加,但是运算速度不变。(这些都是题目中来的,仔细审题就可以)
硬件:
y
=
1
(
1
−
0.7
)
+
(
0.7
/
8
∗
2
)
=
2.91
y=\frac{1}{(1-0.7)+(0.7/8*2)}=2.91
y=(1−0.7)+(0.7/8∗2)1=2.91
软件:设相同速度下,向量化百分比为x。求解方程,即 1/((1-x)+x/8)=2.91, x=0.75。推荐使用软件方法。(why?)
Q3:重要的题


A:
(1) 实际执行总指令除以总时间
M
I
P
S
E
M
U
L
=
(
I
+
F
×
Y
)
/
(
W
×
1
0
6
)
MIPS_{EMUL}=(I+F×Y)/(W×10^6)
MIPSEMUL=(I+F×Y)/(W×106)
M
I
P
S
F
P
U
=
(
I
+
F
)
/
(
B
×
1
0
6
)
MIPS_{FPU}=(I+F)/(B×10^6)
MIPSFPU=(I+F)/(B×106)
(EMUL FPU)是什么意思?
(2) 根据
M
I
P
S
E
M
U
L
=
(
I
+
F
×
Y
)
/
(
W
×
1
0
6
)
MIPS_{EMUL}=(I+F×Y)/(W×10^6)
MIPSEMUL=(I+F×Y)/(W×106) ,
带入数据,
120
=
(
I
+
8
×
1
0
6
×
50
)
/
(
4
×
1
0
6
)
=
>
I
=
80
×
1
0
6
120=(I+8×10^6×50)/(4×10^6) => I=80×10^6
120=(I+8×106×50)/(4×106)=>I=80×106
(3)将上一道题中解出来的I代入式:
80
=
(
80
×
1
0
6
+
8
×
1
0
6
)
/
(
B
×
1
0
6
)
=
>
B
=
1.1
80=(80×10^6 +8×10^6)/(B×10^6) => B=1.1
80=(80×106+8×106)/(B×106)=>B=1.1
(4) 概念:
MFLOPS:megaFLOPS,每秒 1 0 6 10^6 106次浮点运算,相当于每秒一百万次浮点运算
按运行该程序时浮点指令数除以浮点部分所占时间(总时间减去定点部分时间) 来计算
M F L O P S = F ( B − W ∗ I I + F ∗ Y ) ∗ 1 0 6 MFLOPS=\displaystyle\frac{F}{(B-\displaystyle\frac{W*I}{I+F*Y})*10^6} MFLOPS=(B−I+F∗YW∗I)∗106F
解释一下: I + F ∗ Y I+F*Y I+F∗Y表示在无浮点部件时的指令数,包括处理整数和处理浮点两部分。
I
I
+
F
∗
Y
\displaystyle\frac{I}{I+F*Y}
I+F∗YI 表示在有协处理器的基础上,整数指令部分的占比。再乘上总的时间,就是整数部分的时间
(5) 决策正确,因为执行时间缩短了,这才是关键标准??为啥啊
Q4: 
A4:(1) 公式如下(来自书本)

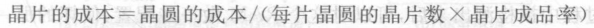
…其他的就不展示了
Q5(第一次做这种题): 对某处理器进行功耗测试,得到如下数据:时钟不翻转,电压1.05V时,电流为500mA;时钟频率为1GHz,电压1.1V时,电流为2500mA。请计算在1.1V下,此处理器的静态功耗以及500MHz下的总功耗。
A5:
功耗:是消耗掉的功率
- 功率P=U∗I,电压U=I∗R 功率单位是W,电压单位是V,电流单位是A
- 时钟不翻转的静态功耗,计算时等效成电阻R ( R = U / I )
- 动态功耗与时钟频率(翻转率)成正比
- 总功耗 = 动态功耗 + 静态功耗
1.1V下静态功耗1.1×1.1/(1.05/0.5)=0.576w 时钟不翻转的静态功耗按电阻算
1.1V下1GHZ时动态功耗为1.1×2.5-0.576=2.174w 动态功耗=总功耗-静态功耗
1.1V 下 0.5GHZ 动态功耗为 2.174×0.5/1=1.087W 动态功耗与翻转率成正比
1.1V 下 0.5GHZ 总功耗为 1.087+0.576=1.663W
Q6:证明以下结论:
(1))N个整数的几何平均小于等于算术平均。
(2)用归一化的SPEC CPU 2000程序分值进行A、B两台计算机的性能比较与所使用的参考机无关
A6:
(1) 首先来看一看什么是几何平均和算术平均吧~
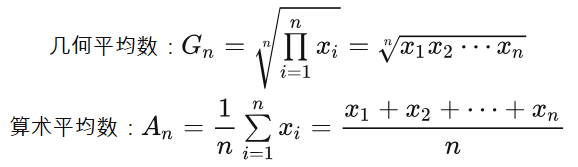
也即是我们要证明:

直接看知乎大佬的吧…(看证明2)
(2) 首先来看一看定义/

证明其实很简单:
 (为啥要开根号呀? 应该是用几何平均做归一化:相乘开根号嘛)
(为啥要开根号呀? 应该是用几何平均做归一化:相乘开根号嘛)
985
Q7…应该不是很重要 不写了hhh
Q8:
补充作业: