前言

本章主要推导一个简单的两层神经网络。
其中公式入口【入口】

---

1.sigmod函数

激活函数我们选择sigmod，其如下：
$$f(x)=\frac{1}{1+e^{-x}}$$
其图形为：

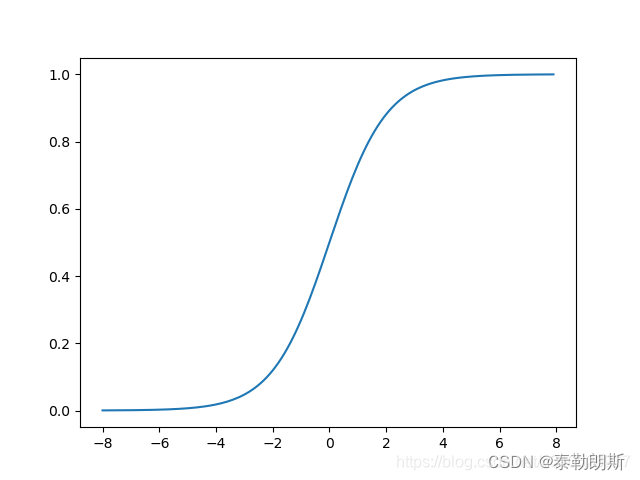
可以用python表示：

def sigmoid(x):
	return 1.0/(1.0+np.exp(-x))

2.sigmoid求导

先看一个复合函数求导：
$$如果y(u)=f(u),u(x)=g(x),那么\frac{dy}{dx}=\frac{dy}{du}\ast \frac{du}{dx}$$
那么对于sigmoid函数求导：
$$\begin{gathered} f(x)=\frac{1}{1+e^{-x}}, \\ 那么假设g(x)=1+e^{-x}, \\ f(x)=\frac{1}{g(x)} \\ f(x{)}^{‘}=\frac{-1}{g(x{)}^2}\ast (-e^{-x})=\frac{e^{-x}}{(1+e^{-x}{)}^2}=f(x)\ast (1-f(x)) \end{gathered}$$
如果用python表达：

def sigmoid_prime(x):
	"""sigmoid 函数的导数"""
	return sigmoid(x)*(1-sigmoid(x))

3.损失函数loss

$$Loss=\frac{1}{2}\ast {(\breve{y}-y)}^2$$
它的导数，
$$Los{s}^{‘}=\breve{y}-y$$

4.神经网络

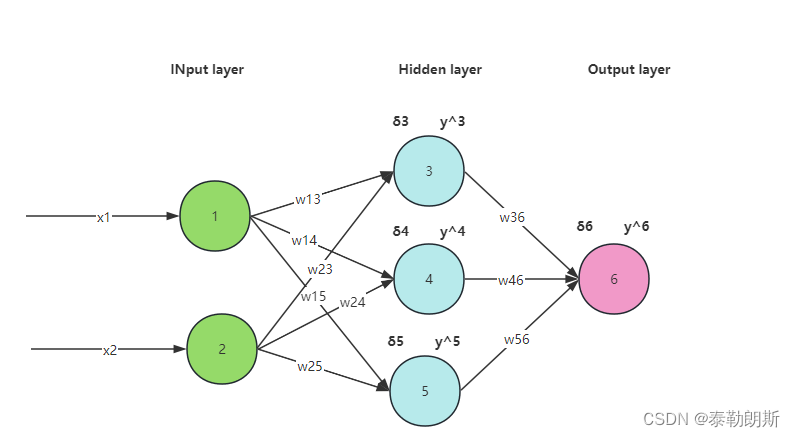
1.神经网络结构

本次我们采用如下神经网络：

2.公式表示-正向传播

$$\begin{gathered} w_{13}\ast x_1+w_{23}\ast x_2+b_1={\sigma }_3,那么\breve{y_3}=sigmoid({\sigma }_3) \\ {w}_{14}\ast x_1+w_{24}\ast x_2+b_2={\sigma }_4,那么\breve{y_4}=sigmoid({\sigma }_4) \\ {w}_{15}\ast x_1+w_{25}\ast x_2+b_3={\sigma }_5,那么\breve{y_5}=sigmoid({\sigma }_5) \\ 同理可得， \\ {w}_{36}\ast \breve{y_3}+w_{46}\ast \breve{y_4}+w_{56}\ast \breve{y_5}+b_4={\sigma }_6,那么\breve{y_6}=sigmoid({\sigma }_6) \end{gathered}$$
上面的公式我们用矩阵表示：
$$\begin{gathered} \left[\begin{array}{cc}{x}_1& x_2\end{array}\right]\cdot \left[\begin{array}{ccc}{w}_{13}& w_{14}& w_{15}\\ w_{23}& w_{24}& w_{25}\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]=\left[\begin{array}{c}{w}_{13}\ast x_1+w_{23}\ast x_2+b_1\\ w_{14}\ast x_1+w_{24}\ast x_2+b_2\\ w_{15}\ast x_1+w_{25}\ast x_2+b_3\end{array}\right]=\left[\begin{array}{c}{\sigma }_3\\ {\sigma }_4\\ {\sigma }_5\end{array}\right] \\ 代入激活函数， \\ \left[\begin{array}{c}sigmoid({\sigma }_3)\\ sigmoid({\sigma }_4)\\ sigmoid({\sigma }_5)\end{array}\right]=\left[\begin{array}{c}\breve{y_3}\\ \breve{y_4}\\ \breve{y_5}\end{array}\right] \\ \left[\begin{array}{ccc}& & \\ \breve{y_3}& \breve{y_4}& \breve{y_5}\end{array}\right]\cdot \left[\begin{array}{c}{w}_{36}\\ w_{46}\\ w_{56}\end{array}\right]+\left[\begin{array}{c}{b}_4\end{array}\right]=\left[\begin{array}{c}{w}_{36}\ast \breve{y_3}+w_{46}\ast \breve{y_4}+w_{56}\ast \breve{y_5}+b_4\end{array}\right]={\sigma }_6 \\ , \\ sigmoid({\sigma }_6)={\breve{y}}_6 \end{gathered}$$

3.梯度计算

1.Loss 函数

$$Loss=\frac{1}{2}\ast {({\breve{y}}_6-y_6)}^2$$

2.梯度

1.反向传播第2-3层

$$\begin{gathered} \left[\begin{array}{c}\frac{\partial l}{\partial w_{36}}\\ \\ \frac{\partial l}{\partial w_{46}}\\ \\ \frac{\partial l}{\partial w_{56}}\end{array}\right]=\left[\begin{array}{c}\frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial w_{36}}\\ \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial w_{46}}\\ \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial w_{56}}\end{array}\right]=\left[\begin{array}{c}({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_3\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_4\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_5\end{array}\right] \\ because, \\ S(x)=\frac{1}{1+e^{-x}} \\ so上面的式子等于, \\ . \\ \left[\begin{array}{c}({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_3\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_4\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast {\breve{y}}_5\end{array}\right] \end{gathered}$$
根据公式2，我们已经知道${\breve{y}}_6$和${\breve{y}}_3$的值，所以上面的权重偏导数就能计算出来了。
下面求bias的偏导数，$\frac{\partial l}{\partial b_4}$.
$$\frac{\partial l}{\partial b_4}=\frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial b_4}=({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))$$

2.反向传播第1-2层

权重

$$\begin{gathered} \left[\begin{array}{cc}\frac{\partial l}{\partial w_{13}}& \frac{\partial l}{\partial w_{23}}\\ & \\ \frac{\partial l}{\partial w_{14}}& \frac{\partial l}{\partial w_{24}}\\ & \\ \frac{\partial l}{\partial w_{15}}& \frac{\partial l}{\partial w_{25}}\end{array}\right]=\left[\begin{array}{cc}\frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_3}\ast \frac{\partial {\breve{y}}_3}{\partial {\sigma }_3}\ast \frac{\partial {\sigma }_3}{\partial w_{13}}& \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_3}\ast \frac{\partial {\breve{y}}_3}{\partial {\sigma }_3}\ast \frac{\partial {\sigma }_3}{\partial w_{23}}\\ & \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_4}\ast \frac{\partial {\breve{y}}_4}{\partial {\sigma }_4}\ast \frac{\partial {\sigma }_4}{\partial w_{14}}& \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_4}\ast \frac{\partial {\breve{y}}_4}{\partial {\sigma }_4}\ast \frac{\partial {\sigma }_4}{\partial w_{24}}\\ & \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_5}\ast \frac{\partial {\breve{y}}_5}{\partial {\sigma }_5}\ast \frac{\partial {\sigma }_5}{\partial w_{15}}& \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_5}\ast \frac{\partial {\breve{y}}_5}{\partial {\sigma }_5}\ast \frac{\partial {\sigma }_5}{\partial w_{25}}\end{array}\right]= \\ . \\ . \\ \left[\begin{array}{cc}({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{36}\ast S({\sigma }_3)\ast (1-S({\sigma }_3))\ast x_1& ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{36}\ast S({\sigma }_3)\ast (1-S({\sigma }_3))\ast x_2\\ & \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{46}\ast S({\sigma }_4)\ast (1-S({\sigma }_4))\ast x_1& ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{46}\ast S({\sigma }_4)\ast (1-S({\sigma }_4))\ast x_2\\ & \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{56}\ast S({\sigma }_5)\ast (1-S({\sigma }_5))\ast x_1& ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{56}\ast S({\sigma }_5)\ast (1-S({\sigma }_5))\ast x_2\end{array}\right] \end{gathered}$$
偏置
$$\begin{gathered} \left[\begin{array}{c}\frac{\partial l}{\partial b_1}\\ \\ \frac{\partial l}{\partial b_2}\\ \\ \frac{\partial l}{\partial b_3}\end{array}\right]=\left[\begin{array}{c}\frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_3}\ast \frac{\partial {\breve{y}}_3}{\partial {\sigma }_3}\ast \frac{\partial {\sigma }_3}{\partial b_1}\\ \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_4}\ast \frac{\partial {\breve{y}}_4}{\partial {\sigma }_4}\ast \frac{\partial {\sigma }_4}{\partial b_2}\\ \\ \frac{\partial l}{\partial {\breve{y}}_6}\ast \frac{\partial {\breve{y}}_6}{\partial {\sigma }_6}\ast \frac{\partial {\sigma }_6}{\partial {\breve{y}}_5}\ast \frac{\partial {\breve{y}}_5}{\partial {\sigma }_5}\ast \frac{\partial {\sigma }_5}{\partial b_3}\end{array}\right]= \\ . \\ \left[\begin{array}{c}({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{36}\ast S({\sigma }_3)\ast (1-S({\sigma }_3))\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{46}\ast S({\sigma }_4)\ast (1-S({\sigma }_4))\\ \\ ({\breve{y}}_6-y_6)\ast S({\sigma }_6)\ast (1-S({\sigma }_6))\ast w_{56}\ast S({\sigma }_5)\ast (1-S({\sigma }_5))\end{array}\right] \end{gathered}$$