递归，搜索与回溯

news2024/11/24 20:39:43

1.汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

//确定子问题处理方式是相同的
//确定递归函数的函数头传参
//确定函数体也就子问题的处理方式
//判断函数出口

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        int n=A.size();
        dfs(A,B,C,n);
    }

    void dfs(vector<int>& A,vector<int>&B ,vector<int>& C,int n){
        if(n==1){
        C.push_back(A.back());//这里一定是要A.back(),可以画一下递归展开图
        A.pop_back();
        return;
        }//函数出口

        dfs(A,C,B,n-1);//不关心如何递归下去的，认为该函数一定能够帮我做到把a上的n-1数据借助c挪动b上

        C.push_back(A.back());//这里一定是要A.back(),可以画一下递归展开图
        A.pop_back();

        dfs(B,A,C,n-1);//同样认为该函数一定能把b上残留的n-1个数据借助a放到c上面
    }
};

2.合并升序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode* newHead=merge(list1,list2);
        return newHead;
    }

    ListNode* merge(ListNode* l1,ListNode* l2){
        if(l1==nullptr) return l2;
        if(l2==nullptr) return l1;


        if(l1->val<l2->val){
            l1->next=merge(l1->next,l2);
            return l1;//返回拼好的头节点
        }

        else{
            l2->next=merge(l2->next,l1);
            return l2;
        }

    }
};

3. 反转链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head==nullptr||head->next==nullptr)return head;
        ListNode* newhead=reverseList(head->next);//认为一定可以返回一个已经逆序的子链表
        head->next->next=head;//让已经逆序的子序列的头节点指向子序列的上一个头节点
        head->next=nullptr;
        return newhead;//这里newhead一直是没有移动过的，一直都是新的链表的头结点。
    }
};

4. 两两交换链表中的节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head==nullptr||head->next==nullptr)
        {
            return head;
        }

        ListNode* new_head=head->next;
        ListNode* tmp=head->next->next;//小心中途修改的问题
        head->next->next=head;
        head->next=swapPairs(tmp);
        return new_head;
    }
};

5. Pow（x,n）

  • -100.0 < x < 100.0
  • -2^31 <= n <= 2^31-1
  • -10^4 <= x^n <= 10^4

本题需要注意负数的情况和超int取值范围的情况

这样会语法报错。。。

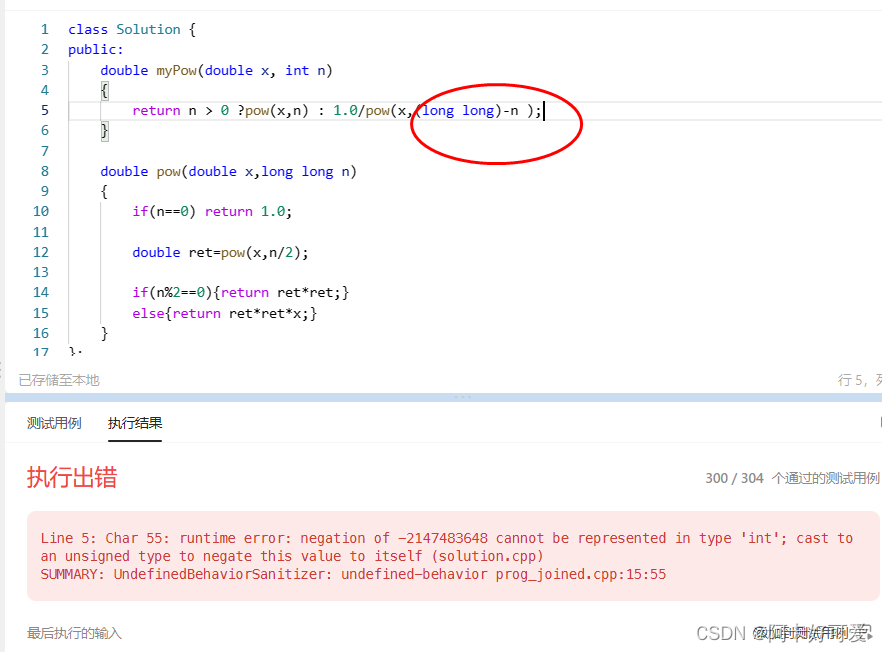
class Solution {
public:
    double myPow(double x, int n) 
    {
        return n > 0 ?pow(x,n) : 1.0/pow(x,-(long long)n );
    }

    double pow(double x,long long n)
    {
        if(n==0) return 1.0;

        double ret=pow(x,n/2);

        if(n%2==0){return ret*ret;}
        else{return ret*ret*x;}
    }
};

6. 布尔逻辑二叉树

class Solution {
public:
    bool evaluateTree(TreeNode* root) {
        if(root->left==nullptr)
        {
            if(root->val==1)return true; 
            else return false;
        }

        bool left=evaluateTree(root->left);
        bool right=evaluateTree(root->right);
        if(root->val==2)
        {
            return left || right;
        }
        else 
        {
            return left && right;
        }

    }
};

7.根到叶子之和 

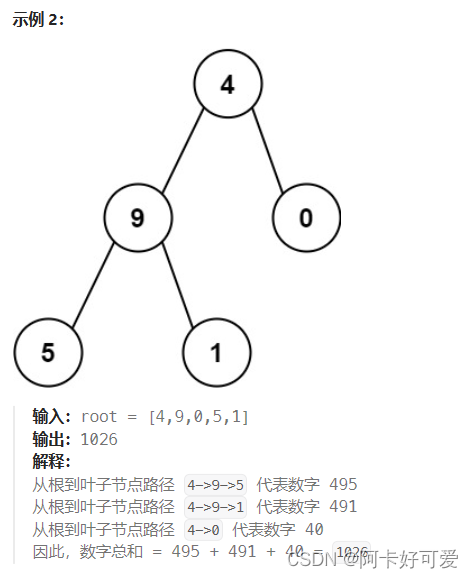
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

//函数头设计，我们认为传入一个节点，那么就会算出此节点到所有节点的数字之和
//函数体：从上一层获得此前的所有数字组合再拼上此层，所以需要多设计一个参数来记录
//函数出口：当没有孩子的时候
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        return dfs(root,0);
    }

    int dfs(TreeNode* root,int presum)
    {
        // if(root==nullptr)
        // {
        //     return presum;题目给的一定是有一个节点
        // }

        presum=presum*10+root->val;
        std::cout<<presum<<std::endl;
        int ret=0;//因为函数的功能是用来计算之和并返回，所以不能直接presum传入，此处presum只是用于记录已经遍历了的数字。

        if(root->left==nullptr&&root->right==nullptr){
            return presum;
        }

        if(root->left) ret+=dfs(root->left,presum);
        if(root->right) ret+= dfs(root->right,presum);

        return ret;
    }
};

8.二叉树剪枝

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//函数体设计
//返回一个已经剪枝的根节点

//函数出口：当自己是空的时候返回空，处理动作一致

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        // if(root==nullptr)
        // {
        //     return nullptr;
        // }

        if(root->left) root->left=pruneTree(root->left);
        if(root->right) root->right=pruneTree(root->right);

        if(root->left==nullptr&&root->right==nullptr&&root->val==0)
        //走到头才算是树枝当树枝被剪完了自己也就是树枝的。
        {
            //delete root;
            root=nullptr;
            // return nullptr;
        }

        return root;
    }
};

9.验证二叉搜索树（注意剪枝）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
long long prev_val=LONG_MIN;

    bool isValidBST(TreeNode* root) {
        if(root==nullptr)
        {
            return true;
        }
        bool left=isValidBST(root->left);

        if(left==false) return false;//剪枝
        
        bool cur=false;
        if(root->val>prev_val)
        {
            prev_val=root->val;
            cur=true;
        }

        if(right==false) return false;//剪枝

        bool right=isValidBST(root->right);
        //cout<< root->val;



        return left&&right&&cur;
    }
};

10. 二叉搜索树第k小的元素（二叉搜索树中序遍历是一个有序序列）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int count;
    int ret;

    int kthSmallest(TreeNode* root, int k) {
        count=k;
        return dfs(root);
    }

    int dfs(TreeNode* root)
    {
        if(root==nullptr){
            return ret;
        }
        ret=dfs(root->left);
        if(count==0)
        {
            return ret;
        }
        ret=root->val;
        count--;
        ret=dfs(root->right);

        return ret;
    }
};

11. 二叉树的所有路径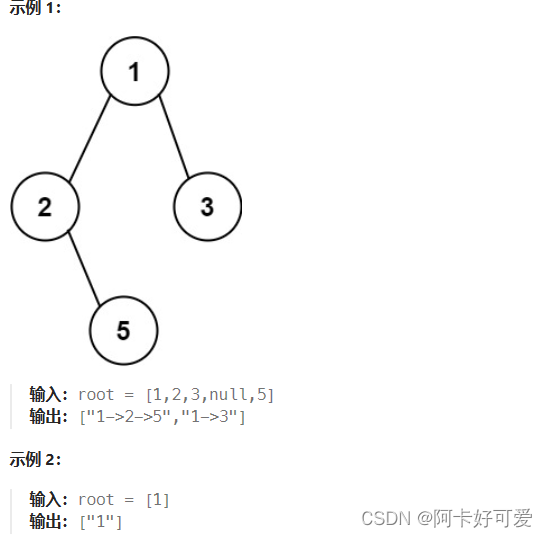

12. 全排列

1.此处path设置为全局变量更好，虽然回溯时需要修改，但是节省一些空间并且效率更高。：

class Solution {
public:

    vector<vector<int>> ret;
    vector<bool> check;//用于记录哪些数字使用过了而达到剪枝的效果，回溯的时候需要把使用过的数字还回去
    vector<int> path;//这里的path最好使用全局变量
    vector<vector<int>> permute(vector<int>& nums) {
        check.resize(nums.size());
        dfs(nums,path);
        return ret;
    }

    void dfs(vector<int>& nums,vector<int> path)
    {
        if(nums.size()==path.size())
        {
            ret.push_back(path);
            return ;
        }

        for(int i=0;i<nums.size();i++)
        {


            if(check[i]==true)
            {
                continue;
            }
            check[i]=true;
            vector<int> tmp=path;
            tmp.push_back(nums[i]);
            dfs(nums,tmp);

            check[i]=false;
        }
    }
};

2. 修改后：

class Solution {
public:

    vector<vector<int>> ret;
    vector<bool> check;//用于记录哪些数字使用过了而达到剪枝的效果，回溯的时候需要把使用过的数字还回去
    vector<int> path;//这里的path最好使用全局变量
    vector<vector<int>> permute(vector<int>& nums) {
        check.resize(nums.size());
        dfs(nums,path);
        return ret;
    }

    void dfs(vector<int>& nums,vector<int>& path)
    {
        if(nums.size()==path.size())
        {
            ret.push_back(path);
            return ;
        }

        for(int i=0;i<nums.size();i++)
        {


            if(check[i]==true)
            {
                continue;
            }
            check[i]=true;
            // vector<int> tmp=path;
            // tmp.push_back(nums[i]);
            path.push_back(nums[i]);
            dfs(nums,path);

            check[i]=false;//向下递归完后恢复现场
            path.pop_back();
        }
    }
};

13. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

13. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> ret;
    string path;
    int i=0;
    vector<string> binaryTreePaths(TreeNode* root) 
    {
        if(root==nullptr) return ret;//假设会传入空，最好不要写在dfs函数里面
        dfs(root,path);
        return ret;
    }

    void dfs(TreeNode* root,string path)
    {
        path+=to_string(root->val);
        if(root->left==nullptr&&root->right==nullptr)
        {
            ret.push_back(path);
            return;
        }
        path+="->";
        if(root->left) dfs(root->left,path);
        if(root->right) dfs(root->right,path);//剪枝，并且达到了不会传入空的效果

    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1034401.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

软件自动化测试工具使用应该注意的事项

软件自动化测试工具使用应该注意的事项

【软件测试面试突击班】如何逼自己一周刷完软件测试八股文教程&#xff0c;刷完面试就稳了&#xff0c;你也可以当高薪软件测试工程师&#xff08;自动化测试&#xff09; 自动化测试正在逐步取代部分手动测试&#xff0c;因为它可以节省时间并提高测试质量。特别是在进行回归测…
阅读更多...
详解Renko图表如何表现价格变动

详解Renko图表如何表现价格变动

相信大多数投资者与FPmarkets澳福一样&#xff0c;都已发现Renko图表与日本烛台图一样&#xff0c;具有上升和下降的特性。增长期间的典型砖块颜色为绿色或白色&#xff0c;而衰退期前的Renko则呈现红色或黑色。 今天&#xff0c;FPmarkets澳福将与各位投资者共同探讨Renko图表…
阅读更多...
小红书AI绘画头像号，私域引流4000+人的暴力流量玩法

小红书AI绘画头像号，私域引流4000+人的暴力流量玩法

本期是赤辰第30期AI项目教程&#xff0c;底部准备了9月粉丝福利&#xff0c;可以免费领取。 今天给大家分享在小红书上强引流项目玩法&#xff1a;AI头像壁纸号&#xff0c;都知道&#xff0c;壁纸/头像/漫改&#xff0c;一直是蓝海项目&#xff0c;流量大且好变现&#xff0c;…
阅读更多...
飞桨EasyDL-Mac本地部署离线SDK-Linux集成Python

飞桨EasyDL-Mac本地部署离线SDK-Linux集成Python

前言&#xff1a;本文对使用飞桨EasyDL桌面版实现本地部署物体检测做一下说明 一、训练模型 如何使用飞桨EasyDL桌面版这里就不再赘述&#xff0c;直接参照官方文档进行物体检测模型训练。 飞桨EasyDL桌面版-用零代码开发实现物体检测https://ai.baidu.com/ai-doc/EASYDL/Tl2…
阅读更多...
内存函数 memcpy 和 memmove 的讲解和模拟实现

内存函数 memcpy 和 memmove 的讲解和模拟实现

目录 一.什么是 memcpy 函数 模拟思路 代码实现 二.什么是 memmove 函数 模拟思路 代码实现 一.什么是 memcpy 函数 我们打开 cplusplus 官网查看&#xff1a; memcpy - C Reference (cplusplus.com) 官方文本显示&#xff1a; 内存复制块 将 num 字节的值从源指向的位置…
阅读更多...
怎样防止员工泄露技术？（十条避免公司泄密的措施）

怎样防止员工泄露技术？（十条避免公司泄密的措施）

在当今信息化社会&#xff0c;公司信息的安全性和保密性显得尤为重要。一旦公司信息泄露&#xff0c;不仅会对公司的经营造成严重影响&#xff0c;还可能引发法律纠纷。因此&#xff0c;采取有效的措施来防止公司信息泄露是非常必要的。以下是一些具体的措施&#xff1a; 部署洞…
阅读更多...
makedown语法及相关语法格式

makedown语法及相关语法格式

这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题&#xff0c;有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…
阅读更多...
Linux学习记录——삼십 socket编程---udp套接字

Linux学习记录——삼십 socket编程---udp套接字

文章目录 UDP套接字简单通信1、服务端1、创建文件&#xff0c;写框架2、用命令行参数调起程序3、服务端运行逻辑 2、客户端1、创建套接字2、发送数据 3、测试4、通信5、加功能1、处理数据2、群聊 6、Windows下socket编程的不同 UDP套接字简单通信 1、服务端 1、创建文件&…
阅读更多...
手动部署 OceanBase 集群

手动部署 OceanBase 集群

手动部署一个 OB 单副本集群&#xff0c;包括一个 OBProxy 节点 部署环境 服务器信息 IP地址 192.168.0.26 网卡名 ifcfg-enp1s0 OS Kylin Linux Advanced Server release V10 CPU 8C 内存 32G 磁盘1 本地盘 /data/1 磁盘2 本地盘 /data/log1 机器和角色划分 …
阅读更多...
Python之使用PySimpleGUI打造桌面应用

Python之使用PySimpleGUI打造桌面应用

PySimpleGUI 是一款比较新的, 基于Python实现的GUI图形库, 他桌面的布局方式采用的是列表方式实现的. Github 仓库地址: github.com/PySimpleGUI… 安装 使用 pip 工具安装即可 shell 复制代码 pip install PySimpleGUI简单的交互 代码 py 复制代码 import PySimpleGUI as …
阅读更多...
LeetCode 416.分割等和子集（动态规划【0-1背包问题】采用一维数组dp:滚动数组）

LeetCode 416.分割等和子集（动态规划【0-1背包问题】采用一维数组dp:滚动数组）

>>往期文章&#xff1a; 解决0-1背包问题&#xff08;方案一&#xff09;:二维dp数组_呵呵哒(&#xffe3;▽&#xffe3;)"的博客-CSDN博客 解决0-1背包问题&#xff08;方案二&#xff09;&#xff1a;一维dp数组&#xff08;滚动数组&#xff09;_呵呵哒(&…
阅读更多...
【前端】零基础快速搞定JavaScript核心知识点

【前端】零基础快速搞定JavaScript核心知识点

【前端】零基础快速搞定JavaScript核心知识点 1.初识JavaScript 1.1.JavaScript语言简介 &#xff08;1&#xff09;简介 JavaScript 是互联网上最流行的脚本语言&#xff0c;这门语言可用于 HTML 和 web&#xff0c;更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机…
阅读更多...
OpenCV直方图的原理与显示、掩膜、均衡化、自适应均衡化

OpenCV直方图的原理与显示、掩膜、均衡化、自适应均衡化

直方图 1 灰度直方图 1.1直方图的绘制和计算 代码实现 import numpy as np import cv2 as cv import matplotlib.pyplot as plt#直接以灰度图的方式读入img cv.imread("lena.png",0)#统计灰度图 histr cv.calcHist([img],[0],None,[256],[0,256]) 使用 OpenCV 的 c…
阅读更多...
list容器排序案例

list容器排序案例

案例描述:将Perspn自定义数据类型进行排序&#xff0c;Person中属性有姓名、年龄、身高 排序规则:按照年龄进行升序&#xff0c;如果年龄相同按照身高进行降序 代码示例 #include <iostream> #include <string.h> #include <iterator> #include <vector…
阅读更多...
java-- 字符串+拼接详解, 性能调优 (底层原理实现)

java-- 字符串+拼接详解, 性能调优 (底层原理实现)

目录 简单了解一下字符串 String类里面是如何存放字符串的? String的不可变性 字符串拼接的方法 1.使用拼接字符串 2. 使用concat 3. 使用StringBuilder 4.StringBuffer 使用字符串拼接的原理 使用concat StringBuilder 效率比较 简单了解一下字符串 字符串在java…
阅读更多...
Flink---5、聚合算子、用户自定义函数、物理分区算子、分流、合流

Flink---5、聚合算子、用户自定义函数、物理分区算子、分流、合流

星光下的赶路人star的个人主页 欲买桂花同载酒&#xff0c;终不似&#xff0c;少年游 文章目录 1、 聚合算子1.1 按键分区&#xff08;KeyBy&#xff09;1.2 简单聚合&#xff08;Sum/Min/MinBy/MaxBy&#xff09;1.3 归约聚合&#xff08;Reduce&#xff09; 2、用户自定义函数…
阅读更多...
redis实战-实现笔记点赞和点赞排行榜

redis实战-实现笔记点赞和点赞排行榜

发布探店笔记 探店笔记类似点评网站的评价&#xff0c;往往是图文结合。对应的表有两个&#xff1a; tb_blog&#xff1a;探店笔记表&#xff0c;包含笔记中的标题、文字、图片等 tb_blog_comments&#xff1a;其他用户对探店笔记的评价 保存笔记service层 Overridepublic Re…
阅读更多...
实例讲解Spring boot动态切换数据源

实例讲解Spring boot动态切换数据源

前言 在公司的系统里&#xff0c;由于数据量较大&#xff0c;所以配置了多个数据源&#xff0c;它会根据用户所在的地区去查询那一个数据库&#xff0c;这样就产生了动态切换数据源的场景。 今天&#xff0c;就模拟一下在主库查询订单信息查询不到的时候&#xff0c;切换数据…
阅读更多...
什么是UWB定位技术？UWB定位的应用场景及功能介绍

什么是UWB定位技术？UWB定位的应用场景及功能介绍

说到定位我们并不陌生&#xff0c;定位技术一直与我们的生活密不可分&#xff0c;比如最常见的车辆导航。 根据使用场景&#xff0c;定位技术分为室内定位和室外定位。 室外定位主要依靠GPS&#xff0c;北斗&#xff0c;GLONASS&#xff0c;伽利略等全球卫星定位导航系统。室内…
阅读更多...
系统集成|第十一章(笔记)

系统集成|第十一章(笔记)

目录 第十一章 项目人力资源管理11.1 项目人力资源管理的定义及有关概念11.2 主要过程11.2.1 编制项目人力资源管理计划11.2.2 组建项目团队11.2.3 建设项目团队11.2.4 管理项目团队 11.3 现代激励理论11.4 项目经理所需具备的影响力11.5 常见问题 上篇&#xff1a;第十章、质量…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023