目录
题目:
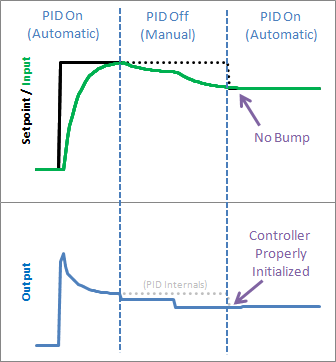
示例:
分析:
代码:
题目:


示例:

分析:
这是一道程序设计类的题目,题目比较长,我稍微概括一下。
构造函数中给我们一个数组,第i个元素表示第i个节点的父节点,让我们以此数组来构造一棵树(不是二叉树)。
类中有三个成员函数,第一个是上锁函数,给我们一个节点值以及一个用户ID,让我们对节点以用户的名义上锁,前提是这个节点没上锁。
第二个是解锁函数,给我们一个节点值和一个用户ID,让我们把这个节点解锁,前提是这个节点之前已经上锁,并且是同一个用户ID上锁的。
第三个是升级函数,给我们节点值和用户ID,要我们把这个节点上锁,并且把这个节点的所有子孙节点都解锁。前提是这个节点的祖先节点没有一个上锁的,并且这个节点的子孙节点至少有一个上锁的。
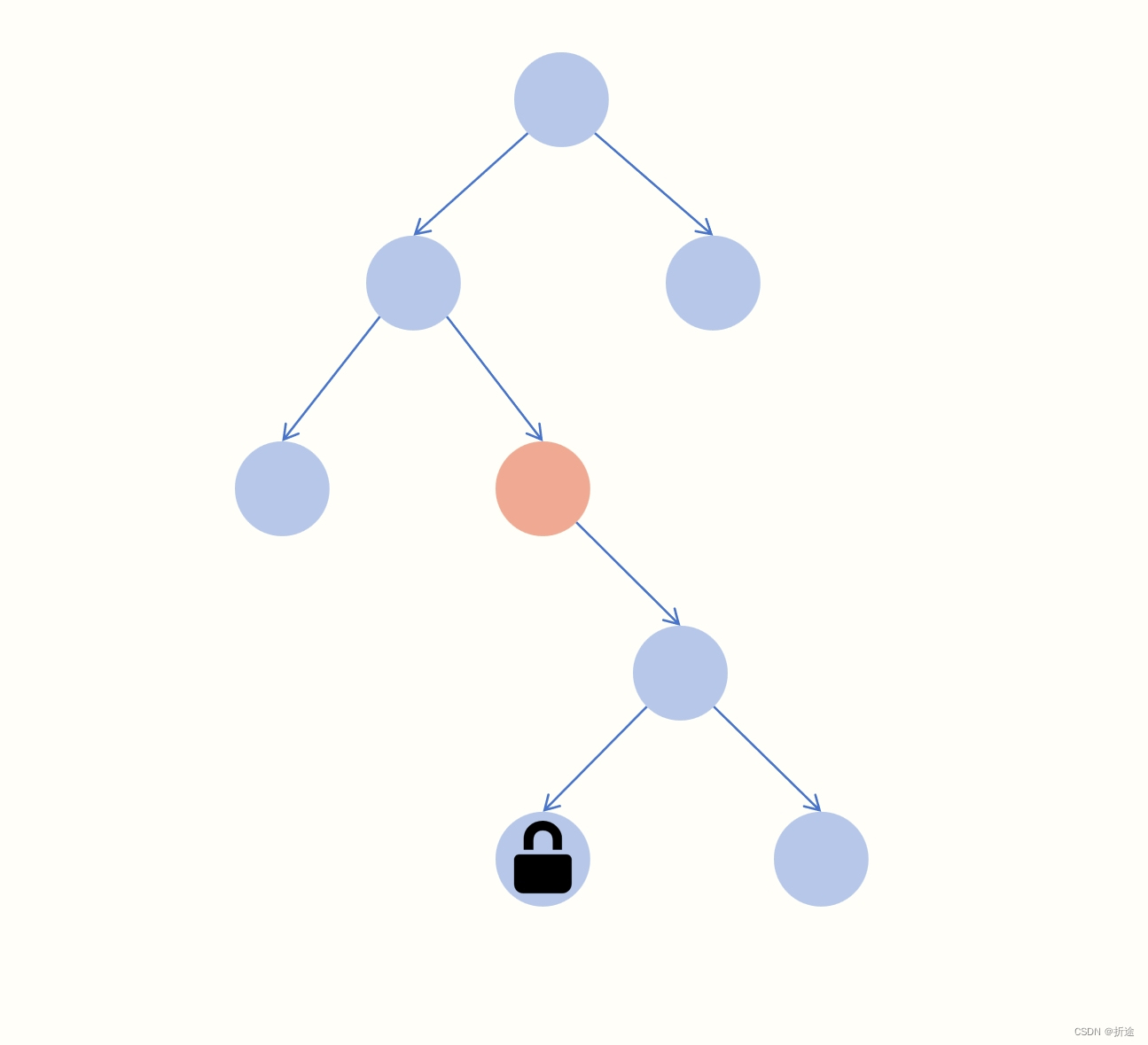
我们来逐个击破,首先是上锁函数,我们只需要拿一个数组来存放上锁关系即可,这个数组的第i个元素表示给节点i上锁的用户,如果是-1则表示这个节点没有上锁。
解锁函数也类似,我们只需要查看给节点上锁的用户是不是当前用户即可。
最后剩下升级函数,一共是三个条件。
第一个是当前节点未上锁,这个好办,我们查询上诉关系数组就行。
第二个是查询子孙节点,要求子孙节点至少有一个上锁,要用到节点的父子关系了,所以我们在构造函数的时候就构建出节点的父子关系,拿一个map来存放每个节点的子节点就行。
寻找子孙节点的时候我们使用递归函数去查询,我使用的是DFS,找哪怕一个上锁的节点我们都返回true表示子孙节点有上锁的,但是我们不是立即返回,因为这个升级函数还要我们把上锁的子孙节点都解锁,因此我们还需要接着往下寻找子孙节点,遇到上锁的我们就解锁。
第三个条件是祖先节点没有上锁的,由于每个节点只会有一个父节点,因此我们不断向上去寻找祖先节点即可,遇到上锁的就返回false。
最后三个条件都满足了,我们再将这个节点以当前用户的名义上锁。
代码:
class LockingTree {
public:
unordered_map<int,vector<int>>sons; //记录每个节点的子节点
vector<int>parent; //记录每个节点的父亲
vector<int>whoLock; //记录每个节点的上锁情况
LockingTree(vector<int>& parent):parent(parent),whoLock(vector<int>(parent.size(),-1)) {
//构建子节点的关系
for(int i=0;i<parent.size();i++){
if(sons.find(parent[i])==sons.end()) sons[parent[i]]=vector<int>(0);
sons[parent[i]].push_back(i);
}
}
bool lock(int num, int user) {
//如果该节点已经上过锁那么不能上锁,反之可以并且修改上锁人
if(whoLock[num]!=-1) return false;
whoLock[num]=user;
return true;
}
bool unlock(int num, int user) {
//如果该节点没有被该用户上锁,那么不能解锁,反之解锁
if(whoLock[num]!=user) return false;
whoLock[num]=-1;
return true;
}
//寻找某节点的父节点是否上锁
bool find(int num){
if(num==-1) return true;
if(whoLock[num]!=-1) return false;
return find(parent[num]);
}
//寻找子节点是否上锁,如果上锁,那么解锁
bool unlockSon(int num){
bool flag=false;
if(whoLock[num]!=-1){
flag=true;
whoLock[num]=-1;
}
for(auto son:sons[num]){
if(unlockSon(son)) flag=true;
}
return flag;
}
bool upgrade(int num, int user) {
//如果该节点已经锁上了那么不能上锁
if(whoLock[num]!=-1) return false;
//如果有上锁的祖先节点那么不能上锁
if(!find(parent[num])) return false;
//如果子孙节点没有一个上锁的,那么不能上锁
if(!unlockSon(num)) return false;
//一切没问题上锁
whoLock[num]=user;
return true;
}
};