文章目录
- 1、 简介
- 2、P 比例调节
- 3、I 积分控制
- 4、D 微分控制
- 5、简单的模拟PID输出代码
- 6、改进
- 6.1 采样时间
- 6.1.1 问题所在
- 6.1.2 解决方案
- 6.1.3 代码
- 6.1.4 结果
- 6.1.5 关于中断的旁注
- 6.1.6 个人总结
- 6.2 微分项出现尖峰
- 6.2.1 问题所在
- 6.2.2 解决方案
- 6.2.3 代码
- 6.2.4 结果
- 6.2.5 个人总结
- 6.3 运行时调整PID参数
- 6.3.1 问题所在
- 6.3.2 解决方案
- 6.3.3 代码
- 6.3.4 结果
- 6.3.5 个人总结
- 6.4 输出限制
- 6.4.1 问题所在
- 6.4.2 解决方案 – 步骤 1
- 6.4.3 解决方案 – 步骤 2
- 6.4.4 代码
- 6.4.5 结果
- 6.4.6 个人总结
- 6.5 开关PID运算
- 6.5.1 问题所在
- 6.5.2 解决方案
- 6.5.3 代码
- 6.5.4 结果
- 6.5.5 个人总结
- 6.6 关PID后再次开启的初始化
- 6.6.1 问题所在
- 6.6.2 解决方案
- 6.6.3 代码
- 6.6.4 结果
- 6.6.5 更新:为什么不是 ITerm=0?
- 6.6.6 个人总结
- 6.6.4 结果
- 6.6.5 更新:为什么不是 ITerm=0?
- 6.6.6 个人总结
文章基本内容来自大神的博客:http://brettbeauregard.com/blog/2011/04/improving-the-beginners-pid-introduction/
1、 简介
PID算法就是将将上次的结果作为一个负反馈,影响到这次输入的结果, 属于闭环控制
PID表示分为:
P:比例环节;I:积分环节;D:微分环节;- p是控制现在,i是纠正曾经,d是管控未来!
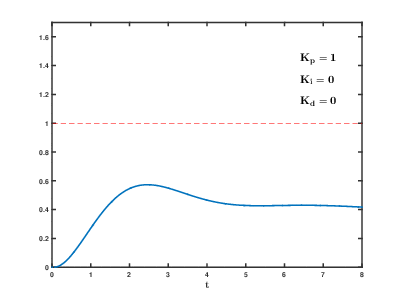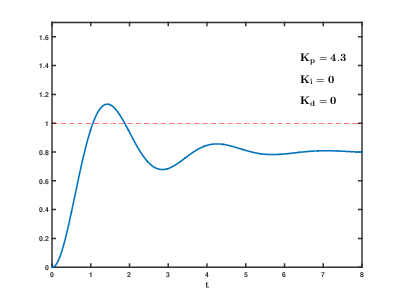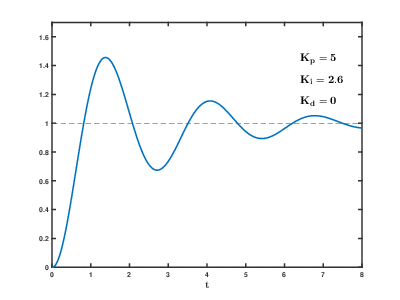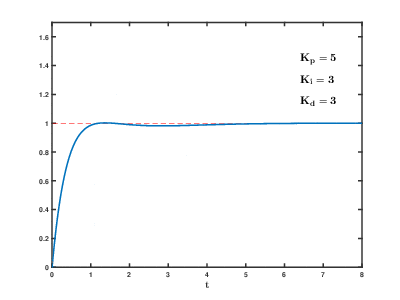
2、P 比例调节
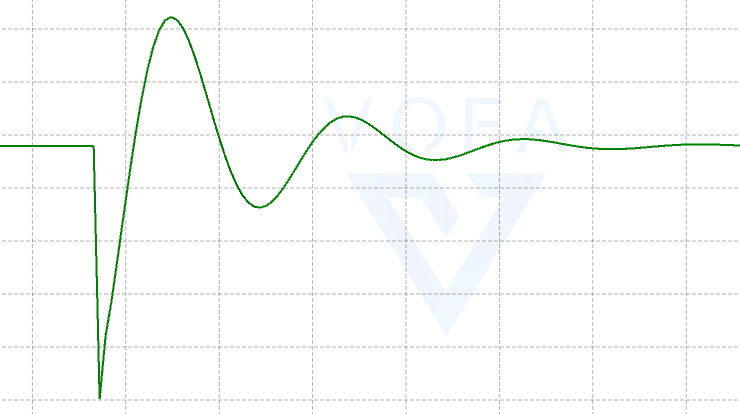
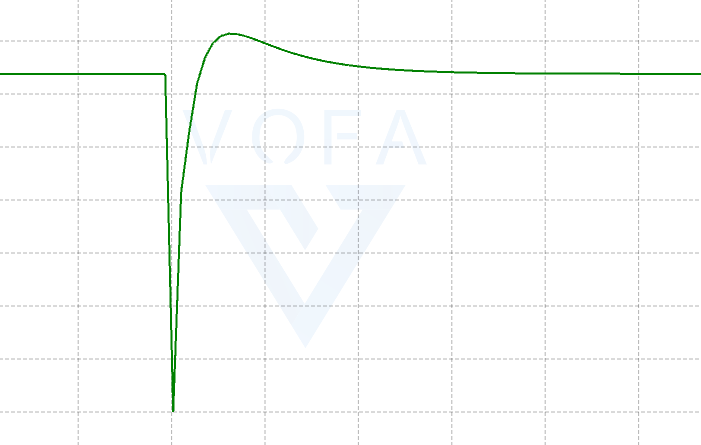
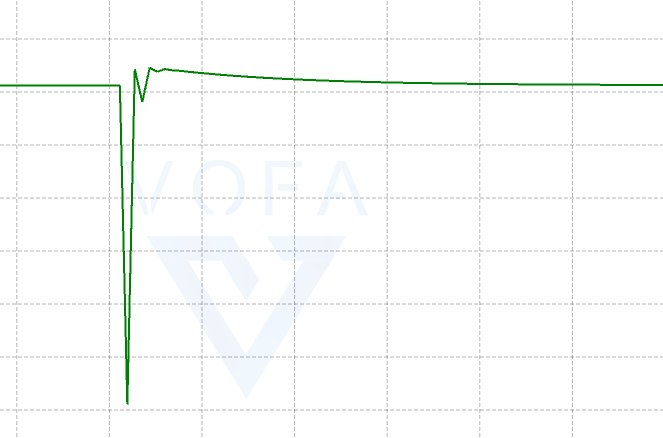
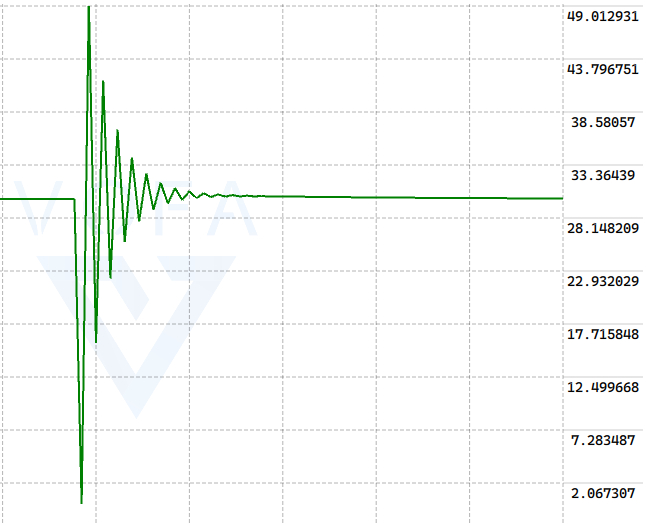
由上图可知,当P越大的时候, 在上升的时候斜率越大, p表示的是此次行进的距离的比例
P比例则是给定一个速度的大致范围
3、I 积分控制
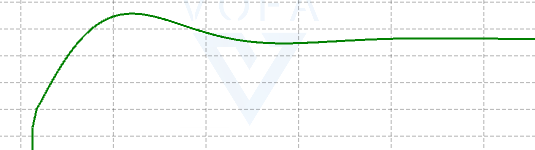
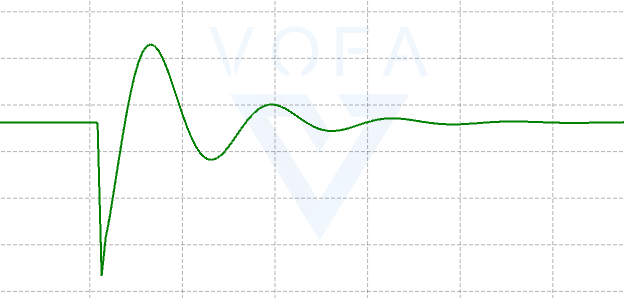
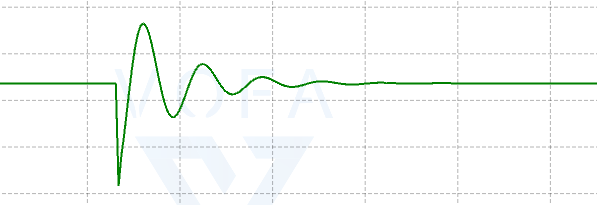
由图可知,I增大时,震荡的幅度越大,I 表示此次行进的距离占之前行进的距离的和的比例
积分则是误差在一定时间内的和
4、D 微分控制


D是误差变化曲线某处的导数,或者说是某一点的斜率
当偏差变化过快,微分环节会输出较大的负数,作为抑制输出继续上升,从而抑制过冲。
5、简单的模拟PID输出代码
简单的模拟代码
void Pid_init() //pid参数初始化
{
P = 0.9;
I = 0.5;
D = 0.01;
Dt = 0.1;
Pre_error = 0;
Integral = 0;
}
double PID_Controller(double setpoint, double pv)//pid的计算
{
Error = setpoint - pv; //计算误差
Pout = Error * P; //算出P项的值
Integral += Error * Dt; //计算面积。高度*时间
Iout = Integral * I;//计算I项的值
Dout = D * (Error - Pre_error) / Dt;//计算D项的值
double output = Iout + Dout + Pout; //计算输出
Pre_error = Error; //记录本次输出的值
return output;
}
//调用
Pid_init();
double pv = 0;
for(int i = 0; i < 200; i++)
{
double inc = PID_Controller(30, pv);
printf("%d,%f,%f,%f,%f,%f,%f\n", i, pv, inc, Pout, Iout, Dout, Integral);
pv += inc;
HAL_Delay(20);
}
6、改进
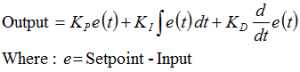
基本代码:
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
void Compute()
{
/*How long since we last calculated*/
unsigned long now = millis();
double timeChange = (double)(now - lastTime);
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += (error * timeChange);
double dErr = (error - lastErr) / timeChange;
/*Compute PID Output*/
Output = kp * error + ki * errSum + kd * dErr;
/*Remember some variables for next time*/
lastErr = error;
lastTime = now;
}
void SetTunings(double Kp, double Ki, double Kd)
{
kp = Kp;
ki = Ki;
kd = Kd;
}
功能提升方法:提高初学者的PID – 简介 « 项目博客 (brettbeauregard.com)
6.1 采样时间
原文:提高初学者的PID – 采样时间 « 项目博客 (brettbeauregard.com)
6.1.1 问题所在
初学者的PID被设计为不规则地调用。这会导致 2 个问题:
- 您不会从 PID 获得一致的行为,因为有时它经常被调用,有时则不然。
- 你需要做额外的数学计算导数和积分,因为它们都依赖于时间的变化。
6.1.2 解决方案
确保定期调用 PID。我决定这样做的方法是指定每个周期调用计算函数。根据预先确定的采样时间,PID 决定是否应立即计算或返回。
一旦我们知道PID正在以恒定的间隔进行评估,也可以简化导数和积分计算。奖金!
6.1.3 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += error;
double dErr = (error - lastErr);
/*Compute PID Output*/
Output = kp * error + ki * errSum + kd * dErr;
/*Remember some variables for next time*/
lastErr = error;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
在第 10 行和第 11 行,算法现在自行决定是否需要计算。此外,因为我们现在知道样本之间的时间是相同的,所以我们不需要不断地乘以时间变化。我们只能适当地调整 Ki 和 Kd(第 31 和 32 行),结果在数学上是等价的,但效率更高。
不过,这样做有点皱褶。如果用户决定在操作过程中更改采样时间,则需要重新调整Ki和Kd以反映此新更改。这就是第 39-42 行的全部内容。
另请注意,我将第 29 行的采样时间转换为秒。严格来说,这不是必需的,但允许用户以 1/秒和 s 为单位输入 Ki 和 Kd,而不是 1/mS 和 mS。
6.1.4 结果
上述更改为我们做了 3 件事
- 无论调用 Compute() 的频率如何,PID 算法都将定期评估 [第 11 行]
- 由于时间减法 [第 10 行],当 millis() 换回 0 时不会有问题。这每 55 天才会发生一次,但我们要防弹还记得吗?
- 我们不再需要乘以时间变化。由于它是一个常量,我们可以将其从计算代码 [第 15+16 行] 中移出,并将其与调优常量 [第 31+32 行] 混为一谈。从数学上讲,它的工作原理相同,但是每次计算PID时都会节省乘法和除法
6.1.5 关于中断的旁注
如果这个PID进入微控制器,则可以为使用中断提出一个很好的论据。SetSampleTime 设置中断频率,然后在需要时调用 Compute。在这种情况下,不需要第 9-12、23 和 24 行。如果您打算用PID影响来做到这一点,那就去做吧!不过,请继续阅读本系列。希望您仍然可以从随后的修改中获得一些好处。
我没有使用中断有三个原因
- 就本系列而言,并不是每个人都能使用中断。
- 如果您希望它同时实现许多PID控制器,事情会变得棘手。
- 老实说,我没有想到。我可能决定在PID库的未来版本中使用中断。
6.1.6 个人总结
在进行pid运算的时候,我们希望两次pid运算的时间间隔相同,因为积分和微分的运算都依赖时间的变化,使用固定的时间计算比较简单,但若是把不固定的时间当作固定的时间进行运算则会影响结果;在实际运用中pid的运算不一定是规则的被调用,所以需要我们根据采样时间区优化。
在运算的时候我们一般使用一个固定值作为Δt,但是实际的采样时间不一定是固定的,所以我们可以使用两次测量的时间差作为Δt,然后根据预设和实际测量出来的Δt的比例来调节Ki和kd。
6.2 微分项出现尖峰
原文:提高初学者的PID – 衍生踢 « 项目博客 (brettbeauregard.com)
衍生踢:尖峰
6.2.1 问题所在
此修改将稍微调整派生项。目标是消除一种称为“衍生踢”的现象。
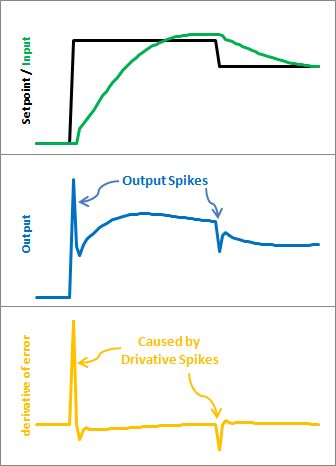
上图说明了问题。由于错误=设定值输入,因此设定值的任何更改都会导致误差的瞬时变化。这种变化的导数是无穷大(在实践中,由于 dt 不是 0,它最终只是一个非常大的数字。该数字被馈入pid方程,从而导致输出中出现不希望的尖峰。幸运的是,有一种简单的方法可以摆脱这种情况。
6.2.2 解决方案

事实证明,误差的导数等于输入的负导数,除非设定值发生变化。这最终是一个完美的解决方案。我们不是加法(Kd * 误差的导数),而是减去(输入的 Kd * 导数)。这称为使用“测量导数”
6.2.3 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += error;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ki * errSum - kd * dInput;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
这里的修改非常简单。我们将 +dError 替换为 -dInput。我们现在不再记住最后一个错误,而是记住最后一个输入
6.2.4 结果
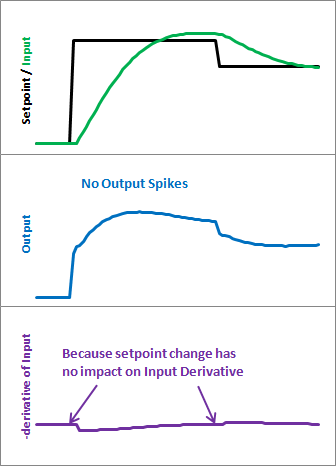
以下是这些修改给我们带来的结果。请注意,输入看起来仍然大致相同。因此,我们获得了相同的性能,但我们不会在每次设定值更改时都发出巨大的输出峰值。
这可能是也可能不是什么大问题。这完全取决于您的应用程序对输出峰值的敏感程度。不过,在我看来,不踢就不需要做更多的工作,所以为什么不把事情做好呢?
6.2.5 个人总结
微分项的值为目标值和当前值的误差再除以时间变化,在6.1中已经改进了时间,所以在此时,时间差Δt应该是一致的,在目标值不变的情况下,
d
e
r
r
d
t
=
d
(
s
e
t
p
o
i
n
t
−
i
n
p
u
t
)
d
t
=
d
s
e
t
p
o
n
i
t
d
t
−
d
i
n
p
u
t
d
t
=
−
d
i
n
p
u
t
d
t
\frac{d_{err}}{dt} = \frac {d_{(setpoint-input)}}{dt}=\frac{d_{setponit}}{dt} -\frac{d_{input}}{dt} = -\frac{d_{input}}{dt}
dtderr=dtd(setpoint−input)=dtdsetponit−dtdinput=−dtdinput因为setpoint一直不变,所以
d
s
e
t
p
o
n
i
t
d
t
\frac{d_{setponit}}{dt}
dtdsetponit为0,因此可以使用
−
d
i
n
p
u
t
d
t
-\frac{d_{input}}{dt}
−dtdinput来代替微分项,这样在位置刚出现变化的时候就不会因为err过大而照成微分项的尖峰。
6.3 运行时调整PID参数
6.3.1 问题所在
在系统运行时更改调谐参数的能力对于任何受人尊敬的PID算法都是必须的。
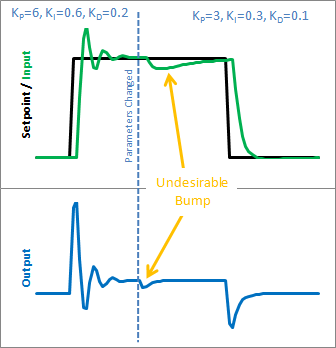
初学者的PID在运行时尝试更改调音,则表现得有点疯狂。让我们看看为什么。以下是上述参数更改前后初学者的PID状态:
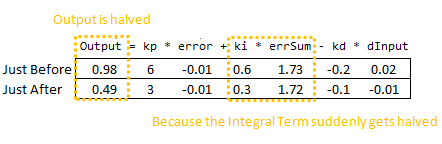
因此,我们可以立即将这种颠簸归咎于积分项(或“I 项”)。这是参数更改时唯一发生巨大变化的东西。为什么会这样?这与初学者对积分的解释有关:

在 Ki 更改之前,这种解释效果很好。然后,突然之间,您将这个新 Ki 乘以您累积的整个误差总和。那不是我们想要的!我们只想影响事情的发展!
6.3.2 解决方案
我知道有几种方法可以解决这个问题。我在上一个库中使用的方法是重新缩放 errSum。基加倍了?将错误总和减半。这样可以防止 I 项发生碰撞,并且它有效。不过有点笨拙,我想出了更优雅的东西。(我不可能是第一个想到这一点的人,但我确实自己想到了。这算该死!
解决方案需要一点基本的代数(或者是微积分?
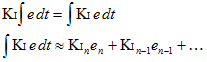
我们不是让 Ki 生活在积分之外,而是把它带入内部。看起来我们什么都没做,但我们会看到在实践中这有很大的不同。
现在,我们取误差并将其乘以当时的 Ki。然后我们存储 THAT 的总和。当 Ki 发生变化时,不会有颠簸,因为可以这么说,所有旧的 Ki 都已经“在银行里”。我们无需额外的数学运算即可顺利转移。这可能会让我成为一个极客,但我认为这很性感。
6.3.3 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
ITerm += (ki * error);
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ITerm - kd * dInput;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
因此,我们将 errSum 变量替换为复合 ITerm 变量 [第 4 行]。它对 Ki*error 求和,而不仅仅是错误 [第 15 行]。此外,由于 Ki 现在被埋在 ITerm 中,因此它已从主 PID 计算 [第 19 行] 中删除。
6.3.4 结果
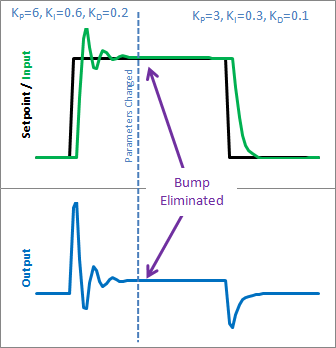
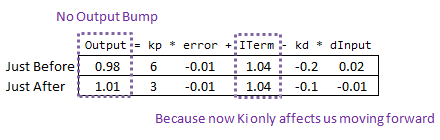
那么这如何解决问题。在更改 ki 之前,它会重新缩放整个误差的总和;我们看到的每一个错误值。使用此代码,以前的错误保持不变,新的 ki 只会影响前进的事情,这正是我们想要的。
6.3.5 个人总结
在运行过程中,突然改变PID的参数时会发生一个波动,主要的原因是在积分项,当曲线趋于稳定时比例项和微分项都是非常小的,只要积分项是可能非常大的。这时候突然改变ki的时候,由于积分项的值比较大,所以在积分项整体的运算结果对输出的影响比较大。
I
t
e
r
m
+
=
e
r
r
∗
Δ
t
Iterm += err * Δt
Iterm+=err∗Δt
I
o
u
t
=
K
i
∗
I
t
e
r
m
I_{out} = K_i * Iterm
Iout=Ki∗Iterm
但是将上式改为
I
t
e
r
m
+
=
K
i
∗
e
r
r
∗
Δ
t
Iterm += K_i * err * Δt
Iterm+=Ki∗err∗Δt
I
o
u
t
=
I
t
e
r
m
I_{out} = Iterm
Iout=Iterm
在 K i K_i Ki不变的情况下两个公式是相等的,但是如果是 K i K_i Ki改变的情况下,公式2将不会带来 I o u t I_out Iout项的剧变。
6.4 输出限制
6.4.1 问题所在

重置发条是一个陷阱,可能比其他任何陷阱都需要更多的初学者。当 PID 认为它可以做一些它不能做的事情时,就会发生这种情况。例如,Arduino上的PWM输出接受0-255之间的值。默认情况下,PID 不知道这一点。如果它认为 300-400-500 会起作用,它会尝试这些值,期望得到它需要的东西。由于实际上该值被固定在 255,因此它只会继续尝试越来越高的数字而无处可去。
问题以奇怪的滞后形式显现出来。上面我们可以看到输出“卷绕”在外部限制以上。当设定值下降时,输出必须在低于255线之前逐渐减少。
6.4.2 解决方案 – 步骤 1

有几种方法可以减轻发条,但我选择的方法如下:告诉PID输出限制是什么。在下面的代码中,您将看到现在有一个 SetOuputLimits 函数。一旦达到任一限制,pid 将停止求和(积分)。它知道没有什么可做的;由于输出不会结束,因此当设定值下降到我们可以做某事的范围内时,我们会立即得到响应。
个人理解记录:
o u t p u t = P o u t + I o u t + D o u t output = P_{out} + I_{out} + D_{out} output=Pout+Iout+Dout
$input = input + output $
在限制 I o u t I_{out} Iout后,由于实际值和目标值之间还存在差距,因此output一直为正值,input一直在增加;但是由于实际值和目标值之间得差越来越小,所以 I o u t I_{out} Iout一直在减小,当 D o u t D_{out} Dout > I o u t I_{out} Iout时,output还在增加,当 D o u t D_{out} Dout < I o u t I_{out} Iout时,output就会减小。
上图的变化就是因此。
6.4.3 解决方案 – 步骤 2
请注意,在上图中,虽然我们摆脱了清盘滞后,但我们并没有一路走来。pid 认为它正在发送的内容和正在发送的内容之间仍然存在差异。为什么?比例项和(在较小程度上)派生项。
即使积分项已被安全钳位,P和D仍然加两美分,产生高于输出限值的结果。在我看来,这是不可接受的。如果用户调用一个名为“SetOutputLimits”的函数,他们必须假设这意味着“输出将保持在这些值内”。因此,对于第 2 步,我们将其作为有效的假设。除了钳位 I 项外,我们还夹紧输出值,使其保持在我们预期的位置。
(注意:你可能会问为什么我们需要同时夹紧两者。如果我们无论如何都要做输出,为什么要单独夹紧积分?如果我们所做的只是钳制输出,积分项将回到增长和增长。虽然输出在升压期间看起来不错,但我们会看到降阶时明显滞后。
6.4.4 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
ITerm+= (ki * error);
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ITerm- kd * dInput;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
void SetOutputLimits(double Min, double Max)
{
if(Min > Max) return;
outMin = Min;
outMax = Max;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
}
添加了一个新函数,允许用户指定输出限制 [第 52-63 行]。这些限值用于箝位I项[17-18]和输出[23-24]
6.4.5 结果
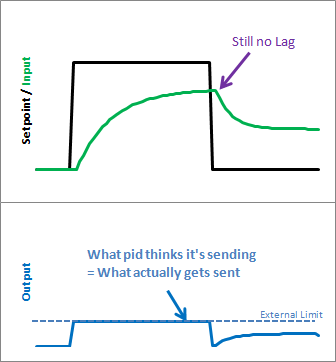
正如我们所看到的,清盘被消除了。此外,输出保留在我们想要的位置。这意味着无需对输出进行外部箝位。如果您希望它的范围从 23 到 167,则可以将其设置为输出限制。
6.4.6 个人总结
在输出一直达不到我们设置的目标值的时候,这时候实际的输出的值限制了计算输出的结果,但是一直达不到目标值,所以积分项的值将会一直累加,计算输出的结果将会非常大,这时候我们应该限制积分项的累加,将其限定为一个固定的范围。当计算输出的值大于最大限制时也可将计算值进行一个限制。这样就避免了计算输出和实际输出不一致,也能做到迅速响应。
6.5 开关PID运算
6.5.1 问题所在
尽管拥有一个PID控制器很好,但有时你并不关心它要说什么。
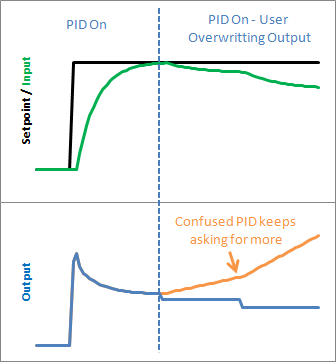
假设在程序中的某个时刻,您希望将输出强制为某个值(例如 0),您当然可以在调用例程中执行此操作:
void loop()
{
Compute();
输出=0;
}
这样,无论 PID 说什么,您都只需覆盖其值。然而,这在实践中是一个糟糕的想法。PID会变得非常困惑:“我一直在移动输出,什么也没发生!什么给?!让我再动一下。因此,当您停止覆盖输出并切换回 PID 时,您可能会立即获得输出值的巨大变化。
6.5.2 解决方案
这个问题的解决方案是有一种关闭和打开PID的方法。这些状态的常用术语是“手动”(我将手动调整值)和“自动”(PID 将自动调整输出)。让我们看看这是如何在代码中完成的:
6.5.3 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
#define MANUAL 0
#define AUTOMATIC 1
void Compute()
{
if(!inAuto) return;
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
ITerm+= (ki * error);
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ITerm- kd * dInput;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
void SetOutputLimits(double Min, double Max)
{
if(Min > Max) return;
outMin = Min;
outMax = Max;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
}
void SetMode(int Mode)
{
inAuto = (Mode == AUTOMATIC);
}
一个相当简单的解决方案。如果未处于自动模式,请立即离开计算函数,而不调整输出或任何内部变量。
6.5.4 结果
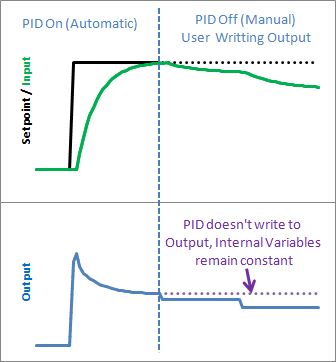
确实,您可以通过不从调用例程调用 Compute 来实现类似的效果,但此解决方案保留了 PID 的工作原理,这正是我们所需要的。通过将事情保持在内部,我们可以跟踪处于哪种模式,更重要的是,当我们更改模式时,它可以让我们知道。这就引出了下一个问题…
6.5.5 个人总结
和下面6.6一起总结
6.6 关PID后再次开启的初始化
6.6.1 问题所在
在上一节中,我们实现了关闭和打开PID的功能。我们关闭了它,但现在让我们看看当我们重新打开它时会发生什么:
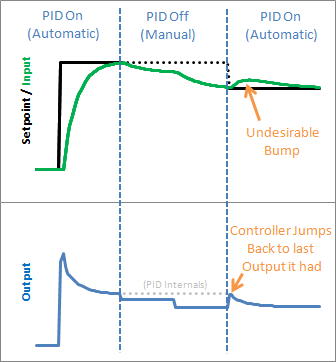
哎呀!PID 跳回到它发送的最后一个输出值,然后从那里开始调整。这会导致我们不希望有的输入凸起。
6.6.2 解决方案
这个很容易修复。由于我们现在知道何时打开(从手动到自动),我们只需要初始化即可平稳过渡。这意味着按摩2个存储的工作变量(ITerm和lastInput)以防止输出跳转。
6.6.3 代码
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
#define MANUAL 0
#define AUTOMATIC 1
void Compute()
{
if(!inAuto) return;
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
ITerm+= (ki * error);
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ITerm- kd * dInput;
if(Output> outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}
void SetOutputLimits(double Min, double Max)
{
if(Min > Max) return;
outMin = Min;
outMax = Max;
if(Output > outMax) Output = outMax;
else if(Output < outMin) Output = outMin;
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
}
void SetMode(int Mode)
{
bool newAuto = (Mode == AUTOMATIC);
if(newAuto && !inAuto)
{ /*we just went from manual to auto*/
Initialize();
}
inAuto = newAuto;
}
void Initialize()
{
lastInput = Input;
ITerm = Output;
if(ITerm> outMax) ITerm= outMax;
else if(ITerm< outMin) ITerm= outMin;
}
我们修改了 SetMode(…) 以检测从手动到自动的转换,并添加了初始化函数。它设置 ITerm=Output 来处理积分项,最后输入 = 输入以防止导数出现峰值。比例项不依赖于过去的任何信息,因此不需要任何初始化。
6.6.4 结果
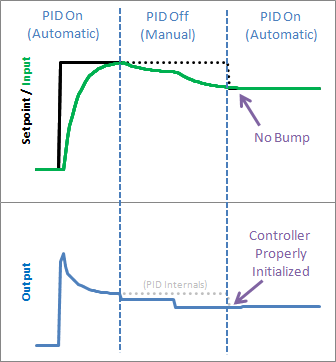
我们从上图中看到,正确的初始化会导致从手动到自动的无颠簸转移:这正是我们所追求的。
下一>>
6.6.5 更新:为什么不是 ITerm=0?
我最近收到很多问题,问为什么我不在初始化时设置 ITerm=0。作为答案,我要求您考虑以下场景:pid 是手动的,用户已将输出设置为 50。一段时间后,该过程稳定到输入 75.2。用户设定值为 75.2 并打开 pid。应该怎么做?
我认为切换到自动后,输出值应保持在 50。由于 P 和 D 项将为零,因此发生这种情况的唯一方法是将 ITerm 初始化为输出值。
如果您处于需要输出初始化为零的情况,则无需更改上面的代码。只需在调用例程中设置 Output=0,然后将 PID 从手动转换为自动。
6.6.6 个人总结
∫
0
t
n
e
r
r
d
x
=
∫
0
t
n
−
1
e
r
r
d
x
+
∫
t
n
−
1
t
e
r
r
d
x
≈
∫
0
t
n
−
1
e
r
r
d
x
+
e
r
r
n
∗
(
t
n
−
t
n
−
1
)
\int_0^{t_n}errdx = \int_0^{t_{n-1}}errdx + \int_{t_{n-1}}^terrdx \approx \int_0^{t_{n-1}}errdx + err_n * (t_n - {t_{n-1}})
∫0tnerrdx=∫0tn−1errdx+∫tn−1terrdx≈∫0tn−1errdx+errn∗(tn−tn−1)
不依赖于过去的任何信息,因此不需要任何初始化。
6.6.4 结果
[外链图片转存中…(img-A5cf55zF-1695383781257)]
我们从上图中看到,正确的初始化会导致从手动到自动的无颠簸转移:这正是我们所追求的。
下一>>
6.6.5 更新:为什么不是 ITerm=0?
我最近收到很多问题,问为什么我不在初始化时设置 ITerm=0。作为答案,我要求您考虑以下场景:pid 是手动的,用户已将输出设置为 50。一段时间后,该过程稳定到输入 75.2。用户设定值为 75.2 并打开 pid。应该怎么做?
我认为切换到自动后,输出值应保持在 50。由于 P 和 D 项将为零,因此发生这种情况的唯一方法是将 ITerm 初始化为输出值。
如果您处于需要输出初始化为零的情况,则无需更改上面的代码。只需在调用例程中设置 Output=0,然后将 PID 从手动转换为自动。
6.6.6 个人总结
∫ 0 t n e r r d x = ∫ 0 t n − 1 e r r d x + ∫ t n − 1 t e r r d x ≈ ∫ 0 t n − 1 e r r d x + e r r n ∗ ( t n − t n − 1 ) \int_0^{t_n}errdx = \int_0^{t_{n-1}}errdx + \int_{t_{n-1}}^terrdx \approx \int_0^{t_{n-1}}errdx + err_n * (t_n - {t_{n-1}}) ∫0tnerrdx=∫0tn−1errdx+∫tn−1terrdx≈∫0tn−1errdx+errn∗(tn−tn−1)