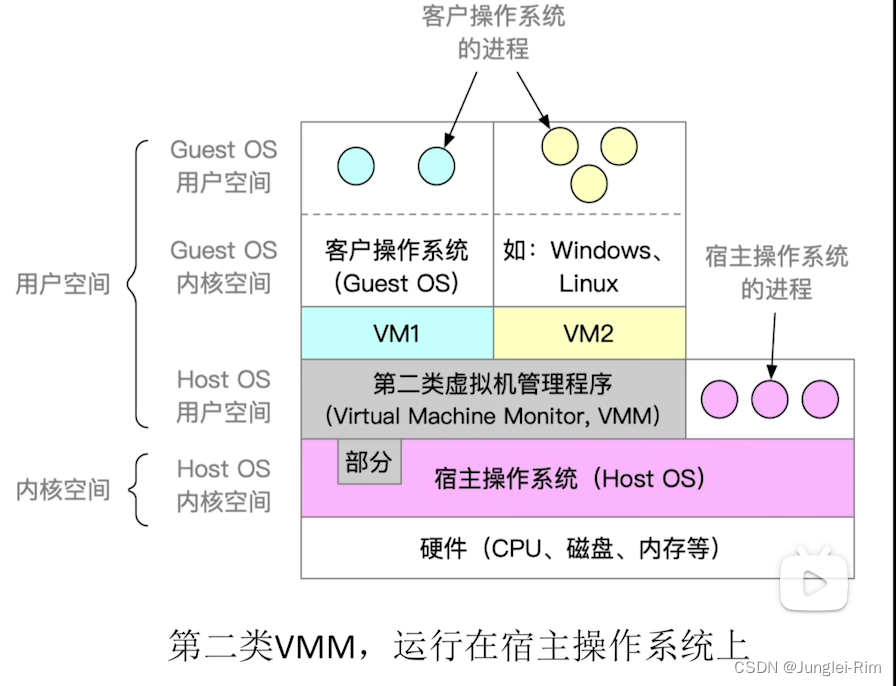
文章目录
- 一、背景
- 二、BA problem的观测性问题
- 1、不可观方向
- 2、解决方案
- 3、优化问题中信息矩阵物理意义
- 三、Keyframe-based Visual-Inertial SLAM的观测性问题
- 1、不可观问题
- 2、解决方案
- 四、MSCKF观测性分析
- 1、观测性分析
- 2、解决方案
- 3、小结
一、背景
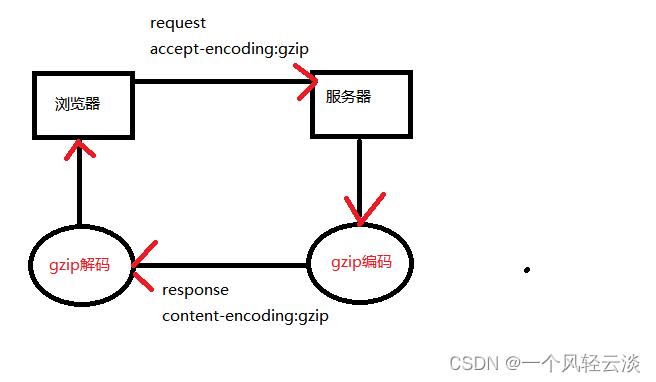
本文档分析以下VINS中的观测性问题,内容源自于前段时间自己的一次PPT分享,阅读观赏性不佳,后续优化
二、BA problem的观测性问题
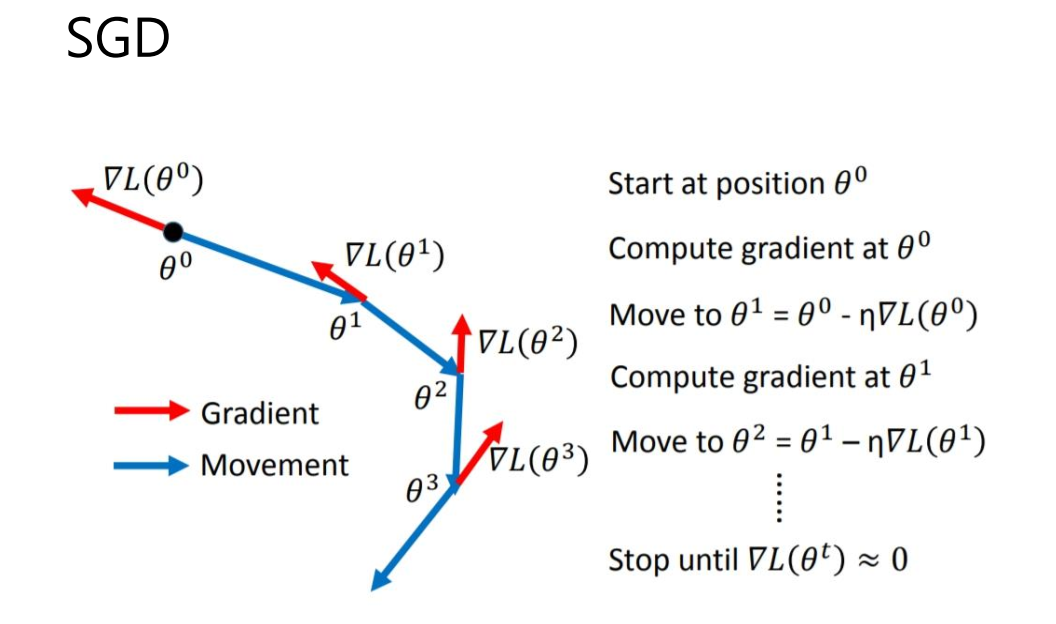
1、不可观方向

边缘化过程可以表示为:
此时对应的因子图为:
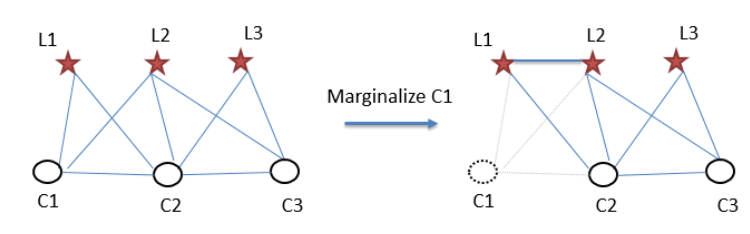
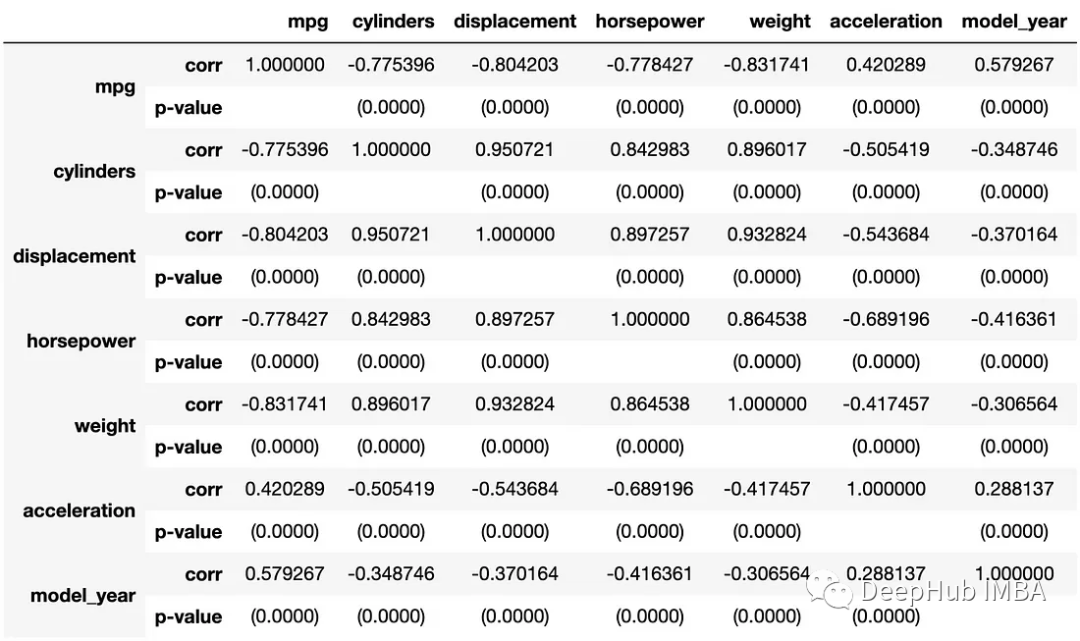
对信息矩阵SVD分解,奇异值最后 7 维接近 0, 表明零空间的维度为 7.

这里的不可观问题会导致BA问题求解出现数值问题,下面介绍解决方案。
2、解决方案
方案一: 使用 LM 算法,加阻尼因子使得系统满秩,可求解,但是求得的结果可能会往零空间变化。

优化完成后,可以看到最终特征点的估计值与真值比较吻合,但第一帧相机的原点不再是( 0,0,0),说明向零空间发生了漂移。
方案二:添加先验约束,增加系统的可观性。实现方式:固定第一帧和第二帧位姿(fix 一个相机 pose 和一个特征点)

实验结果:

方案三:On the Comparison of Gauge Freedom Handling in Optimization-based Visual-Inertial State Estimation
以VIO系统为例,有4dof不可观
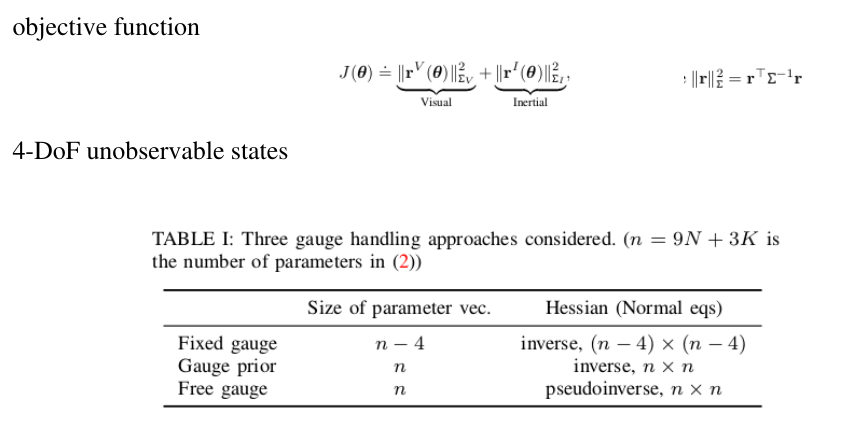
可以采用下面三种解决方案:

实验结果:

- 这三种方法的准确度几乎相同。
- 在prior gauge方法中,需要选择适当的先验权重以避免增加计算成本。
- 在适当的权重值下,prior gauge方法与fixed gauge方法具有几乎相同的性能(精度和计算成本)。
- free gauge略快于其他方法,因为它需要较少的迭代就能收敛
理论上按vins的做法需要在每一次滑窗ba中固定第一帧位姿,实际代码中vins-fusion没有固定第一帧的位姿,而且优化完,把第一帧的delta pose再乘回每一帧,保证第一帧不动,但又由于roll 和 pitch是全局能观的,所以乘delta pose的时候里面旋转只有yaw角。
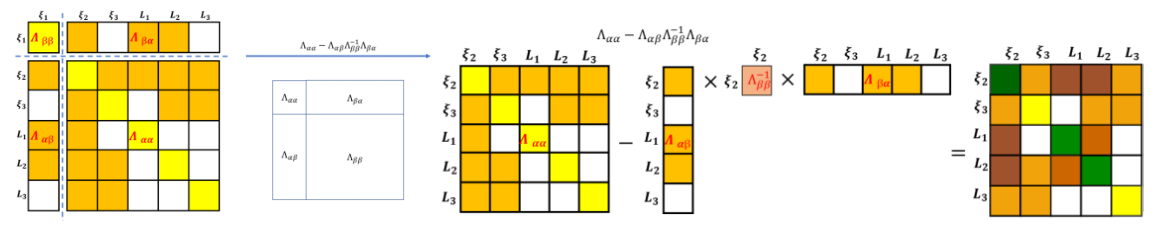
3、优化问题中信息矩阵物理意义
the uncertainty in the free gauge case (Fig. .9a) is “distributed”over all the positions (cf. Fig. 1a). This is due to the fact that the free gauge approach is not fixed to any reference frame. Therefore, the uncertainties directly read from the free gauge covariance matrix are not interpretable in a geometrically-meaningful way.
简单讲,来自free gauge approach的参数协方差与其他方法不同,不能直接以有意义的方式解释。可以通过线性变换将free gauge approach的协方差转化为gauge fixation approach。下面是转换方法。


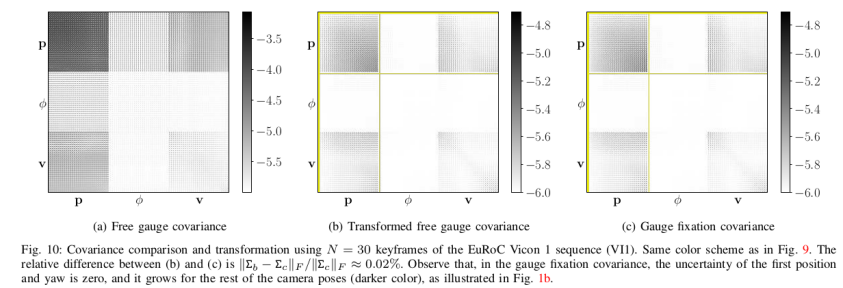
这里颜色越深表示置信度越低,可以看到,相当于认为第一帧很准确,后面是局部窗口内每一帧的相对置信度。
三、Keyframe-based Visual-Inertial SLAM的观测性问题
1、不可观问题

这里对应为下图:能量函数为0的解由以前的一条曲线变成了一个点,不确定性的东西变得确定了,即不可观的状态变量变得可观了,说明我们人为的引入了错误的信息。

2、解决方案
这个问题的解决方案就是使用FEJ :
- 边缘化时,被边缘化的变量的jacobian不再更新,但留在窗口内的而其他变量的jacobian需要使用和边缘化时一样的线性化点(最初线性点),即优化迭代过程中该jacobian不再进行更新, 这意味着,优化迭代过程中 H 矩阵一直不变,但b会改变。
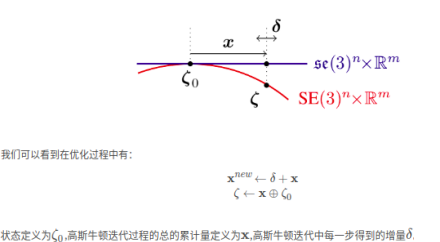
考虑到:

因此,FEJ实现时:

不可观的状态变量变得可观的问题解决之后,就是不可观的变量如何解决。
理论上vins按照gauge fixation的做法需要在每一次滑窗ba中固定第一帧位姿,实际代码中vins没有固定第一帧的位姿,而且优化完,把第一帧的delta pose再乘回每一帧,保证第一帧不动,但又由于roll 和 pitch是全局能观的,所以乘delta pose的时候里面旋转只有yaw角,使用的是free gauge的方法。
四、MSCKF观测性分析
1、观测性分析
 注:积分公式和离散化公式,带 yl和sl积分符号的是积分公式(Li Mingyang和Shelley论文前部分推导),而代码中实际用的不带积分符号的离散化公式
注:积分公式和离散化公式,带 yl和sl积分符号的是积分公式(Li Mingyang和Shelley论文前部分推导),而代码中实际用的不带积分符号的离散化公式
理想情况下的能观性矩阵:

具体计算结果为:

之所以称之为理想,是因为这里线性化点都是真值。
在理想情况下,能观性矩阵的零空间为:

实际情况下的能观性矩阵

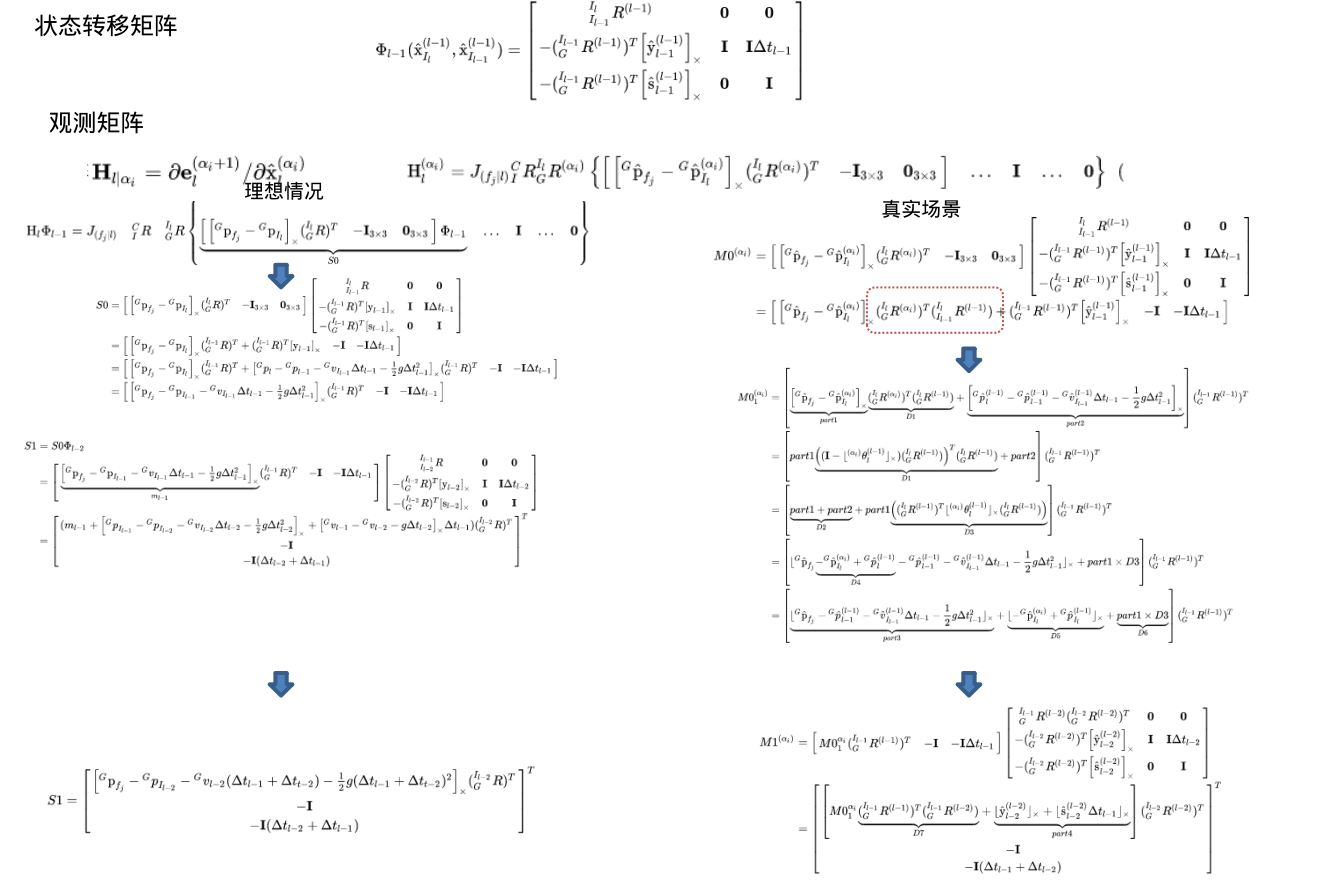
2、解决方案
这里使用FEJ来解决观测性问题,具体实现而言


两个零空间并不相同,但物理意义一样:
- 前三维影响IMU系的位置和特征点的位置,相当于把整个系统的位置shift起来了;
- 最后一个维度影响以重力轴为旋转轴的旋转,也就是世界系的yaw方向,也相当于在yaw方向上shift了整个系统;
下面是为什么是这4个自由度的理论推导:

3、小结
-
零空间:SLAM中的零空间其实是整个优化问题的零空间,而不是说是优化中某个节点的零空间。就是说整个优化问题存在不可观的维度,这个不可观的维度会通过优化问题进而影响到某个节点的优化,导致那个节点出现问题,常见的比如说纯视觉SLAM在转弯的时候,尺度会突然变化。
-
FEJ:FEJ通过固定节点的优化方向,来保证整个系统能观矩阵的零空间一直保持一致,换言之,如果k时刻的状态确定,则整个系统的pos和yaw不可观表现为当前状态和起点的状态是紧密相关的,如果不进行FEJ,yaw错误的变得可观,那么当前yaw和起点状态相关性变弱,此时所有状态的不确定性被低估了
-
不可观的状态变量变得可观的问题解决之后,就是不可观的维度如何解决,OpenVINS采用的是gauge prior的方式。给定初始yaw和位置一个比较高的置信度,此时FEJ引起的协方差变化很小,对精度影响也很小,但协方差物理意义更加明确