一、题目大意

我们有N（N<=35）个元素，从中选取一个子集，使得它的元素求和的绝对值最小，如果有多个可行解，选择元素最小的。

输出最优子集的元素总和绝对值，和最优子集元素的数量。

二、解题思路

我们把前一半，后一半数组分开考虑。

我们利用二进制递增的思路（0001,0010,0011...1111），把后一半数组的所有子集求和给算出来（去掉空集），同时记录每个子集的元素数量。

之后根据子集的sum进行排序，然后利用双指针，把所有sum相等的子集的元素数量更新为 同等sum下最小的元素数量。

然后利用二进制枚举前半部分数组（包括空集），对于每一个左半部分的元素和leftSum，去后半部分数组里二分找 -leftSum，（这个二分的思想就是找到后半部分最小子集元素和不小于 -leftSum的第一个下标），然后把二分的结果idx和idx-1都判断下，计算左右子集和的绝对值，和元素数量。更新ans。

需要注意的是我们去掉了右边为空集的情况，所以要额外判断下只使用左边元素的情况。

我也是很菜了，这个题目WA了60多次，写了6天，最后绝对不用pair了，自己写结构体，也不用lower_bound了，自己写二分，然后再结合自己想出来的尺取法，过了这道题。

过程中没有查看题解，没有搜过答案，但是去看了STL中pair的源码和Comparator的源码，还看了下《挑战程序设计》的“超大背包问题”的源码，其实不应该去看这些，影响到了进步和思考的进程，看完STL源码和白书后决定不用pair和lower_bound了，手写二分底层实现，手写双指针优化，终究是过了。

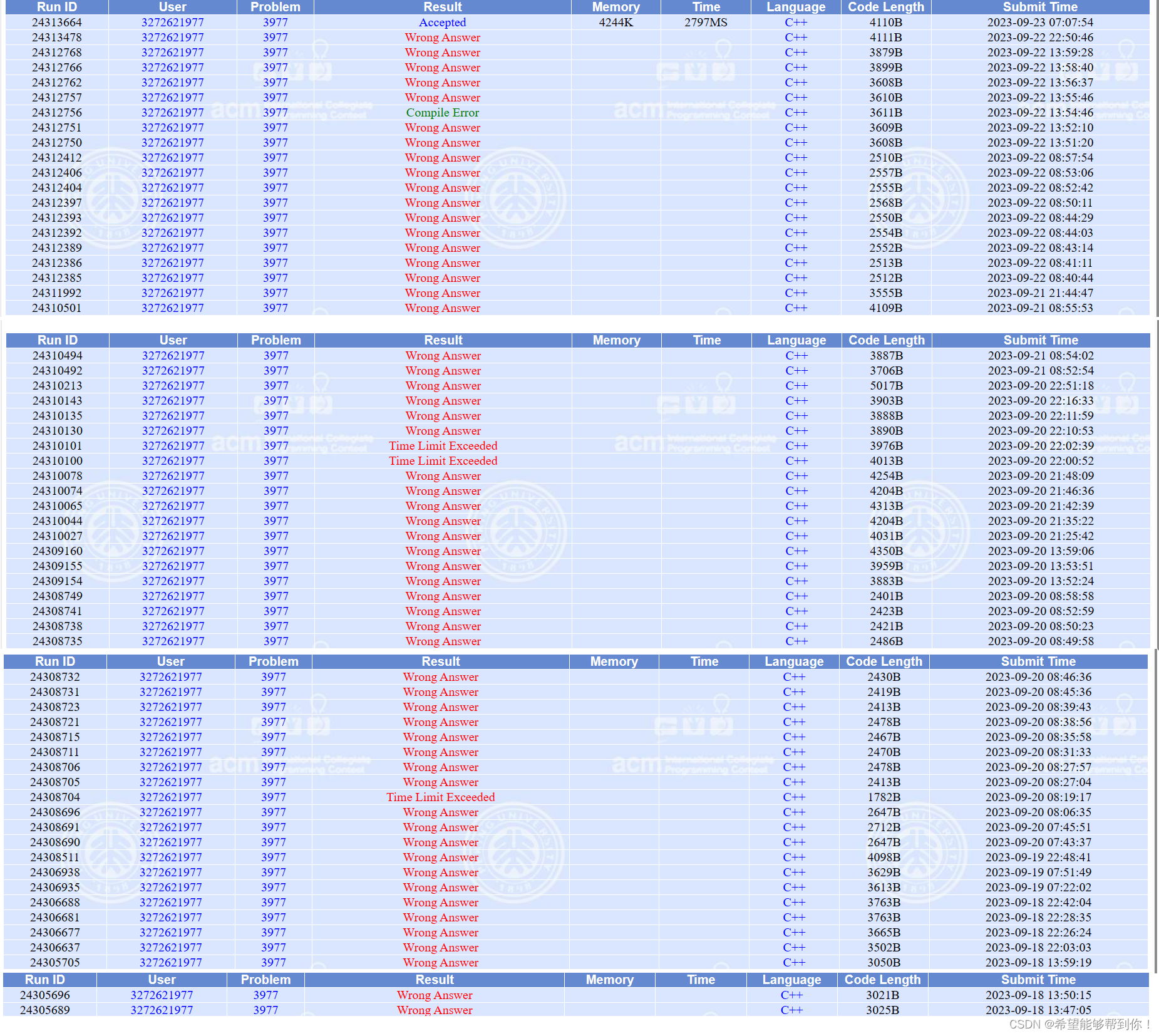
可以说我是非常菜了，自己摸爬滚打总结的一套代码分享在下面。

过了以后查过题解，我这个他们那个map那个复杂一些，因为用了自定义结构体，双指针和手写二分底层实现，但是比它快了5倍吧，源码分享给大家。

三、代码

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
struct Node
{
    int cnt;
    ll sum;
    Node(ll sum = 0LL, int cnt = 0) : sum(sum), cnt(cnt) {}
};
Node rightNodes[262150];
int towPow[27], n, rightLen, leftLen, rightPow, leftPow, ansCnt;
ll num[40], ans, inf = 0x3f3f3f3f3f3f3f3fLL;
void initTwoPow()
{
    towPow[0] = 1;
    for (int i = 1; i <= 21; i++)
    {
        towPow[i] = towPow[i - 1] * 2;
    }
}
bool compareNode(const Node &a, const Node &b)
{
    return a.sum < b.sum;
}
ll absVal(ll a)
{
    if (a >= 0LL)
    {
        return a;
    }
    else
    {
        return a * (-1LL);
    }
}
void input()
{
    ans = 0LL;
    for (int i = 0; i < n; i++)
    {
        scanf("%lld", &num[i]);
        ans = ans + num[i];
    }
    ans = absVal(ans);
    ansCnt = n;
    leftLen = n / 2;
    rightLen = n - leftLen;
    leftPow = towPow[leftLen];
    rightPow = towPow[rightLen];
}
void calcRightSubsetBesideEmptySet()
{
    for (int i = 1; i < rightPow; i++)
    {
        rightNodes[i - 1].sum = 0LL;
        rightNodes[i - 1].cnt = 0;
        for (int j = 0; j < rightLen; j++)
        {
            if ((i & towPow[j]) == towPow[j])
            {
                rightNodes[i - 1].sum = rightNodes[i - 1].sum + num[leftLen + j];
                rightNodes[i - 1].cnt = rightNodes[i - 1].cnt + 1;
            }
        }
    }
    rightNodes[rightPow - 1].sum = inf;
    rightNodes[rightPow - 1].cnt = n + 1;
    sort(rightNodes, rightNodes + rightPow, compareNode);
}
void minimizeCntByTwoPosinter()
{
    int l = 0, r = 1, optCnt = -1;
    while (true)
    {
        while (r < rightPow && rightNodes[r].sum != rightNodes[l].sum)
        {
            l++;
            r++;
        }
        optCnt = rightNodes[l].cnt;
        while (r < rightPow && rightNodes[r].sum == rightNodes[l].sum)
        {
            optCnt = min(optCnt, rightNodes[r].cnt);
            r++;
        }
        while ((l + 1) < r)
        {
            rightNodes[l++].cnt = optCnt;
        }
        if (r == rightPow)
        {
            break;
        }
    }
}
int binarySearch(ll leftSum)
{
    int l = -1, r = rightPow;
    while (l + 1 < r)
    {
        int mid = (l + r) / 2;
        if (rightNodes[mid].sum < leftSum)
        {
            l = mid;
        }
        else
        {
            r = mid;
        }
    }
    return (l + 1);
}
void solve()
{
    ll lSum = 0LL;
    int lCnt = 0;
    for (int i = 0; i < leftPow; i++)
    {
        lSum = 0LL;
        lCnt = 0;
        for (int j = 0; j < leftLen; j++)
        {
            if ((i & towPow[j]) == towPow[j])
            {
                lSum = lSum + num[j];
                lCnt = lCnt + 1;
            }
        }
        if (lCnt != 0 && absVal(lSum) < ans)
        {
            ans = absVal(lSum);
            ansCnt = lCnt;
        }
        else if (lCnt != 0 && absVal(lSum) == ans && lCnt < ansCnt)
        {
            ansCnt = lCnt;
        }
        int idx = binarySearch(lSum * (-1LL));
        if ((idx + 1) < rightPow && absVal(rightNodes[idx].sum + lSum) < ans)
        {
            ans = absVal(rightNodes[idx].sum + lSum);
            ansCnt = rightNodes[idx].cnt + lCnt;
        }
        else if ((idx + 1) < rightPow && absVal(rightNodes[idx].sum + lSum) == ans && (rightNodes[idx].cnt + lCnt) < ansCnt)
        {
            ansCnt = rightNodes[idx].cnt + lCnt;
        }
        idx--;
        if (idx >= 0 && absVal(rightNodes[idx].sum + lSum) < ans)
        {
            ans = absVal(rightNodes[idx].sum + lSum);
            ansCnt = rightNodes[idx].cnt + lCnt;
        }
        else if (idx >= 0 && absVal(rightNodes[idx].sum + lSum) == ans && (rightNodes[idx].cnt + lCnt) < ansCnt)
        {
            ansCnt = rightNodes[idx].cnt + lCnt;
        }
    }
}
int main()
{
    initTwoPow();
    while (true)
    {
        scanf("%d", &n);
        if (n == 0)
        {
            break;
        }
        input();
        calcRightSubsetBesideEmptySet();
        minimizeCntByTwoPosinter();
        solve();
        printf("%lld %d\n", ans, ansCnt);
    }
    return 0;
}