目录

一、逻辑回归

二、逻辑回归的代价函数

三、梯度下降法

---

一、逻辑回归

逻辑回归是一种常用的二分类算法，用于将输入数据映射到一个概率输出，表示为属于某个类别的概率。它基于线性回归模型，并使用了sigmoid函数作为激活函数。

假设我们有一个二分类问题，其中输入特征为x，对应的样本标签为y（0或1）。逻辑回归的目标是根据输入特征x预测样本标签y的概率。

逻辑回归模型可以表示为：

z = w * x + b

其中，w是权重向量，x是输入特征向量，b是偏置。这部分与线性回归模型相似。

不同之处在于，逻辑回归模型还引入了一个sigmoid函数（也称为逻辑函数）g(z)，用于将线性模型的输出z映射到0和1之间的概率值。sigmoid函数的数学表达式如下：

g(z) = 1 / (1 + e^(-z))

通过将线性模型的输出z传入sigmoid函数，得到的结果g(z)表示样本属于正类的概率。反之，1 - g(z)表示样本属于负类的概率。

在训练阶段，我们需要通过最大似然估计或者梯度下降等优化方法来找到最优的权重向量w和偏置b，使得模型的预测结果与实际标签尽可能地接近。

训练过程中的损失函数通常采用交叉熵损失（cross-entropy loss），它可以衡量实际概率分布与预测概率分布之间的差异。通过最小化损失函数，我们可以更新权重向量w和偏置b，以提高模型的预测准确性。

在预测阶段，给定新的输入特征x，我们可以使用训练好的权重向量w和偏置b，将其代入逻辑回归模型，并通过sigmoid函数计算输出概率g(z)。一般而言，如果g(z)大于等于0.5，则我们将样本预测为正类；如果g(z)小于0.5，则预测为负类。

二、逻辑回归的代价函数

逻辑回归模型的代价函数（Cost Function）通常使用交叉熵损失函数（Cross-Entropy Loss）来衡量实际概率分布与模型预测概率分布之间的差异。

假设我们有一个训练集包含m个样本，每个样本的输入特征为x，对应的真实标签为y（0或1）。逻辑回归的目标是找到最优的权重向量w和偏置b，使得模型的预测结果尽可能接近真实标签。

对于每个样本i，逻辑回归模型的预测值表示为y_hat_i，它是通过将输入特征x_i代入逻辑回归模型中计算得到的。预测值y_hat_i可以看作样本i属于正类的概率。

交叉熵损失函数的数学表达式如下：

J(w, b) = - (1/m) * Σ(y_i * log(y_hat_i) + (1-y_i) * log(1-y_hat_i))

其中，J(w, b)表示代价函数，w和b表示权重向量和偏置，m表示样本数量，y_i表示第i个样本的真实标签，y_hat_i表示对应的预测值。

交叉熵损失函数由两部分组成。当真实标签y_i为1时，第一部分y_i * log(y_hat_i)用于衡量模型对正类样本的预测准确性。当真实标签y_i为0时，第二部分(1-y_i) * log(1-y_hat_i)用于衡量模型对负类样本的预测准确性。

代价函数J(w, b)可以看作是对所有样本的预测误差进行平均后取反的结果。我们的目标是通过最小化代价函数来找到最优的权重向量w和偏置b，使得模型的预测结果与真实标签尽可能接近。

在训练阶段，通常使用梯度下降等优化算法来更新权重向量w和偏置b，以最小化代价函数。通过不断迭代优化，逻辑回归模型能够逐渐提高对样本标签的预测准确性。

三、梯度下降法

梯度下降法（Gradient Descent）是一种常用的优化算法，用于最小化代价函数（Cost Function）或损失函数。在逻辑回归等机器学习模型中，梯度下降法常用于更新模型参数，以找到使代价函数最小化的权重和偏置。

梯度下降法的基本思想是通过迭代更新参数，沿着代价函数的负梯度方向移动，以逐步接近代价函数的最小值。具体而言，梯度下降法包括以下步骤：

1. 初始化参数：将权重向量w和偏置b初始化为任意值。

2. 计算梯度：对于每个参数，计算代价函数关于该参数的偏导数（梯度）。这可以使用链式法则来计算，根据代价函数的形式不同而有所不同。

3. 更新参数：根据梯度的方向和学习率（learning rate），更新参数的值。学习率决定了每次参数更新的步长，较大的学习率可能导致无法收敛，而较小的学习率可能导致收敛速度过慢。

4. 重复步骤2和3：重复计算梯度和更新参数的过程，直到达到停止条件。停止条件可以是达到一定的迭代次数，或者代价函数的变化小于某个阈值等。

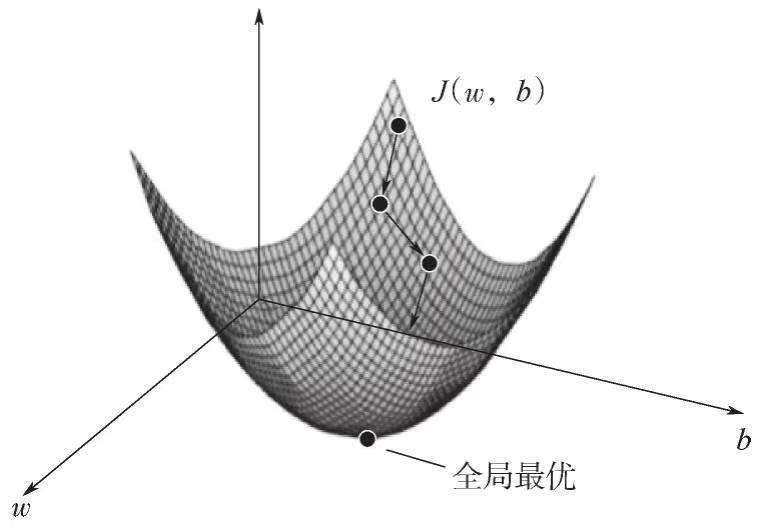
添加图片注释，不超过 140 字（可选）

在逻辑回归中，梯度下降法的目标是最小化代价函数。通过不断更新权重向量w和偏置b，使得模型的预测结果与真实标签尽可能接近。通过迭代优化过程，梯度下降法可以找到局部最优解或接近最优解的参数值，从而提高模型的准确性。

需要注意的是，梯度下降法有多种变体，例如批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-Batch Gradient Descent）。它们的区别在于每次更新参数时使用的样本数量。批量梯度下降使用整个训练集，随机梯度下降使用单个样本，而小批量梯度下降使用一小部分样本来计算梯度和更新参数。不同的变体在收敛速度和计算效率上可能会有所差异。