二、零钱兑换 II 

518. 零钱兑换 II - 力扣（LeetCode）

被选物品之间不需要满足特定关系，只需要选择物品，以达到「全局最优」或者「特定状态」即可。

同时硬币相当于我们的物品，每种硬币可以选择「无限次」，很自然的想到「完全背包」。

这时候可以将「完全背包」的状态定义搬过来进行“微调”：

定义 f[i][j]为考虑前 iii 件物品，凑成总和为 jjj 的方案数量。

为了方便初始化，我们一般让 f[0][x] 代表不考虑任何物品的情况。

因此我们有显而易见的初始化条件：f[0][0]=1，其余 f[0][x]=0。

代表当没有任何硬币的时候，存在凑成总和为 0 的方案数量为 1；凑成其他总和的方案不存在。

当「状态定义」与「基本初始化」有了之后，我们不失一般性的考虑 f[i][j] 该如何转移。

对于第 i 个硬币我们有两种决策方案：

不使用该硬币：
f[i−1][j]

使用该硬币：由于每个硬币可以被选择多次（容量允许的情况下），因此方案数量应当是选择「任意个」该硬币的方案总和：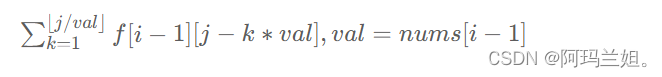

class Solution {
    public int change(int cnt, int[] cs) {
        int n = cs.length;
        int[][] f = new int[n + 1][cnt + 1];
        f[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            int val = cs[i - 1];
            for (int j = 0; j <= cnt; j++) {
                f[i][j] = f[i - 1][j];
                for (int k = 1; k * val <= j; k++) {
                    f[i][j] += f[i - 1][j - k * val];  
                }
            }
        }
        return f[n][cnt];
    }
}

三、组合总和 Ⅳ  

377. 组合总和 Ⅳ - 力扣（LeetCode）

emmmmm看官方题解吧377. 组合总和 Ⅳ - 力扣（LeetCode）