课程地址和说明
线性代数实现p4
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
本节是第四篇,由于CSDN限制,只能被迫拆分
矩阵计算
矩阵的导数运算
向量对向量求导的基本运算规则
已知向量函数 y → = f → ( x → ) \overrightarrow y=\overrightarrow {f}(\overrightarrow x) y=f(x)与向量 x → = [ x 1 x 2 ⋮ x m ] m × 1 \overrightarrow x=\begin{bmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{m} \end{bmatrix}_{m\times 1} x= x1x2⋮xm m×1
- 当
y
→
=
a
→
\overrightarrow y=\overrightarrow a
y=a,且
a
→
\overrightarrow a
a不是
x
→
\overrightarrow x
x的函数(即
a
→
\overrightarrow a
a中没有分量和
x
→
\overrightarrow x
x相关)时,则有:
∂ y → ∂ x → = [ ∂ f ( x → ) ∂ x 1 ∂ f ( x → ) ∂ x 2 ⋮ ∂ f ( x → ) ∂ x m ] = [ 0 0 ⋮ 0 ] = 0 → \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}= \begin{bmatrix} \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{1}}}\\ \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{2}}}\\ \vdots \\ \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{m}}} \end{bmatrix}=\begin{bmatrix} 0\\ 0\\ \vdots \\ 0 \end{bmatrix}=\overrightarrow 0 ∂x∂y= ∂x1∂f(x)∂x2∂f(x)⋮∂xm∂f(x) = 00⋮0 =0 - 当
y
→
=
x
→
\overrightarrow y=\overrightarrow x
y=x时,即
y
→
=
[
f
1
(
x
→
)
f
2
(
x
→
)
⋮
f
m
(
x
→
)
]
=
[
x
1
x
2
⋮
x
m
]
\overrightarrow y=\begin{bmatrix} f_{1}(\overrightarrow x) \\ f_{2}(\overrightarrow x) \\ \vdots \\ f_{m}(\overrightarrow x) \end{bmatrix}=\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{m} \end{bmatrix}
y=
f1(x)f2(x)⋮fm(x)
=
x1x2⋮xm
,则有:
∂ y → ∂ x → = [ ∂ f ( x → ) ∂ x 1 ∂ f ( x → ) ∂ x 2 ⋮ ∂ f ( x → ) ∂ x m ] = [ ∂ f 1 ( x → ) ∂ x 1 ∂ f 2 ( x → ) ∂ x 1 … ∂ f n ( x → ) ∂ x 1 ∂ f 1 ( x → ) ∂ x 2 ∂ f 2 ( x → ) ∂ x 2 … ∂ f n ( x → ) ∂ x 2 ⋮ ⋮ ⋱ ⋮ ∂ f 1 ( x → ) ∂ x m ∂ f 2 ( x → ) ∂ x m … ∂ f n ( x → ) ∂ x m ] m × n = [ 1 0 … 0 0 1 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … 1 ] = I 或 E (单位矩阵的两种不同记号,含义一致) \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}= \begin{bmatrix} \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{1}}}\\ \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{2}}}\\ \vdots \\ \frac{\partial {{f}(\overrightarrow x)}}{\partial {x_{m}}} \end{bmatrix}=\begin{bmatrix} \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{1}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{1}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{1}}} \\ \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{2}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{2}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{2}}} \\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{m}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{m}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{m}}} \end{bmatrix}_{m\times n}=\begin{bmatrix} 1& 0&\dots &0 \\ 0& 1& \dots &0 \\ \vdots & \vdots & \ddots &\vdots \\ 0 & 0& \dots &1 \end{bmatrix}=\bm{I}或\bm{E}(单位矩阵的两种不同记号,含义一致) ∂x∂y= ∂x1∂f(x)∂x2∂f(x)⋮∂xm∂f(x) = ∂x1∂f1(x)∂x2∂f1(x)⋮∂xm∂f1(x)∂x1∂f2(x)∂x2∂f2(x)⋮∂xm∂f2(x)……⋱…∂x1∂fn(x)∂x2∂fn(x)⋮∂xm∂fn(x) m×n= 10⋮001⋮0……⋱…00⋮1 =I或E(单位矩阵的两种不同记号,含义一致) - 当
y
→
=
A
x
→
\overrightarrow y=\bm{A}\overrightarrow {x}
y=Ax,
A
=
[
a
11
a
12
⋯
a
1
m
a
21
a
22
⋯
a
2
m
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
m
]
\bm{A}=\begin{bmatrix} a_{11}&a_{12} & \cdots & a_{1m}\\ a_{21}&a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots &\vdots \\ a_{m1}&a_{m2} & \cdots & a_{mm} \end{bmatrix}
A=
a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1ma2m⋮amm
,则有:
∂ y → ∂ x → = ∂ A x → ∂ x → = A T (按分母布局) \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=\frac{\partial {\bm{A}\overrightarrow x}}{\partial {\overrightarrow x}} =\bm{A}^{T}(按分母布局) ∂x∂y=∂x∂Ax=AT(按分母布局)
∂ y → ∂ x → = ∂ A x → ∂ x → = A (按分子布局) \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=\frac{\partial {\bm{A}\overrightarrow x}}{\partial {\overrightarrow x}} =\bm{A}(按分子布局) ∂x∂y=∂x∂Ax=A(按分子布局)
(证明见本节第三篇) - 当
y
→
=
x
→
T
A
\overrightarrow y=\overrightarrow {x}^{T}\bm{A}
y=xTA,
A
=
[
a
11
a
12
⋯
a
1
m
a
21
a
22
⋯
a
2
m
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
m
]
\bm{A}=\begin{bmatrix} a_{11}&a_{12} & \cdots & a_{1m}\\ a_{21}&a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots &\vdots \\ a_{m1}&a_{m2} & \cdots & a_{mm} \end{bmatrix}
A=
a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1ma2m⋮amm
,
y → = x → T A = [ x 1 , x 2 , … , x m ] ⋅ [ a 11 a 12 ⋯ a 1 m a 21 a 22 ⋯ a 2 m ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m m ] = [ a 11 x 1 + a 21 x 2 + ⋯ + a m 1 x m , a 12 x 1 + a 22 x 2 + ⋯ + a m 2 x m , … , a 1 m x 1 + a 2 m x 2 + ⋯ + a m m x m ] \overrightarrow y=\overrightarrow {x}^{T}\bm{A}=\begin{bmatrix} x_{1}, & x_{2} ,& \dots ,& x_{m} \end{bmatrix}\cdot \begin{bmatrix} a_{11}&a_{12} & \cdots & a_{1m}\\ a_{21}&a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots &\vdots \\ a_{m1}&a_{m2} & \cdots & a_{mm} \end{bmatrix}=\begin{bmatrix} a_{11}x_{1}+a_{21}x_{2}+\dots +a_{m1}x_{m}, & a_{12}x_{1}+a_{22}x_{2}+\dots +a_{m2}x_{m} ,& \dots ,& a_{1m}x_{1}+a_{2m}x_{2}+\dots +a_{mm}x_{m} \end{bmatrix} y=xTA=[x1,x2,…,xm]⋅ a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1ma2m⋮amm =[a11x1+a21x2+⋯+am1xm,a12x1+a22x2+⋯+am2xm,…,a1mx1+a2mx2+⋯+ammxm],所以按一一对应法则只能理解成(这里行向量列向量混用了,没办法) y → = [ f 1 ( x → ) f 2 ( x → ) ⋮ f m ( x → ) ] = [ a 11 x 1 + a 21 x 2 + ⋯ + a m 1 x m a 12 x 1 + a 22 x 2 + ⋯ + a m 2 x m ⋮ a 1 m x 1 + a 2 m x 2 + ⋯ + a m m x m ] \overrightarrow y=\begin{bmatrix} f_{1}(\overrightarrow x) \\ f_{2}(\overrightarrow x) \\ \vdots \\ f_{m}(\overrightarrow x) \end{bmatrix}=\begin{bmatrix} a_{11}x_{1}+a_{21}x_{2}+\dots +a_{m1}x_{m}\\ a_{12}x_{1}+a_{22}x_{2}+\dots +a_{m2}x_{m}\\ \vdots \\ a_{1m}x_{1}+a_{2m}x_{2}+\dots +a_{mm}x_{m} \end{bmatrix} y= f1(x)f2(x)⋮fm(x) = a11x1+a21x2+⋯+am1xma12x1+a22x2+⋯+am2xm⋮a1mx1+a2mx2+⋯+ammxm ,则有:
∂ y → ∂ x → = ∂ x → T A ∂ x → = [ ∂ f 1 ( x → ) ∂ x 1 ∂ f 2 ( x → ) ∂ x 1 … ∂ f n ( x → ) ∂ x 1 ∂ f 1 ( x → ) ∂ x 2 ∂ f 2 ( x → ) ∂ x 2 … ∂ f n ( x → ) ∂ x 2 ⋮ ⋮ ⋱ ⋮ ∂ f 1 ( x → ) ∂ x m ∂ f 2 ( x → ) ∂ x m … ∂ f n ( x → ) ∂ x m ] = [ a 11 a 21 … a m 1 a 12 a 22 … a m 2 ⋮ ⋮ ⋱ ⋮ a 1 m a 2 m … a m m ] = A T \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=\frac{\partial {\overrightarrow {x}^{T}\bm{A}}}{\partial {\overrightarrow x}} =\begin{bmatrix} \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{1}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{1}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{1}}} \\ \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{2}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{2}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{2}}} \\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial {{f_{1}}(\overrightarrow x)}}{\partial {x_{m}}}& \frac{\partial {{f_{2}}(\overrightarrow x)}}{\partial {x_{m}}} & \dots &\frac{\partial {{f_{n}}(\overrightarrow x)}}{\partial {x_{m}}} \end{bmatrix}=\begin{bmatrix} a_{11}& a_{21}&\dots &a_{m1} \\ a_{12}& a_{22}& \dots &a_{m2} \\ \vdots & \vdots & \ddots &\vdots \\ a_{1m}& a_{2m}& \dots &a_{mm} \end{bmatrix}=\bm{A}^{T} ∂x∂y=∂x∂xTA= ∂x1∂f1(x)∂x2∂f1(x)⋮∂xm∂f1(x)∂x1∂f2(x)∂x2∂f2(x)⋮∂xm∂f2(x)……⋱…∂x1∂fn(x)∂x2∂fn(x)⋮∂xm∂fn(x) = a11a12⋮a1ma21a22⋮a2m……⋱…am1am2⋮amm =AT - 当
y
→
=
a
u
→
\overrightarrow y=a\overrightarrow u
y=au,
a
a
a是任意常数,
u
→
=
u
→
(
x
→
)
\overrightarrow u=\overrightarrow {u}(\overrightarrow x)
u=u(x),则有:
∂ y → ∂ x → = a ∂ u → ∂ x → = \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=a\frac{\partial {\overrightarrow u}}{\partial\overrightarrow x}= ∂x∂y=a∂x∂u= - 当
y
→
=
A
u
→
\overrightarrow y=\bm{A}\overrightarrow u
y=Au,
u
→
=
u
→
(
x
→
)
\overrightarrow u=\overrightarrow {u}(\overrightarrow x)
u=u(x),
A
\bm{A}
A中的元素与
x
→
\overrightarrow x
x中的元素无关系,则有:
∂ y → ∂ x → = A ∂ u → ∂ x → = \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=\bm{A}\frac{\partial {\overrightarrow u}}{\partial\overrightarrow x}= ∂x∂y=A∂x∂u= - 当
y
→
=
u
→
+
v
→
\overrightarrow y=\overrightarrow u+\overrightarrow v
y=u+v时,
u
→
=
u
→
(
x
→
)
,
v
→
=
v
→
(
x
→
)
\overrightarrow u = \overrightarrow {u}(\overrightarrow x),\overrightarrow v = \overrightarrow {v}(\overrightarrow x)
u=u(x),v=v(x),则有:
∂ y → ∂ x → = ∂ u → ∂ x → + ∂ v → ∂ x → = \frac{\partial {\overrightarrow y}}{\partial\overrightarrow x}=\frac{\partial {\overrightarrow u}}{\partial\overrightarrow x}+\frac{\partial {\overrightarrow v}}{\partial\overrightarrow x}= ∂x∂y=∂x∂u+∂x∂v=
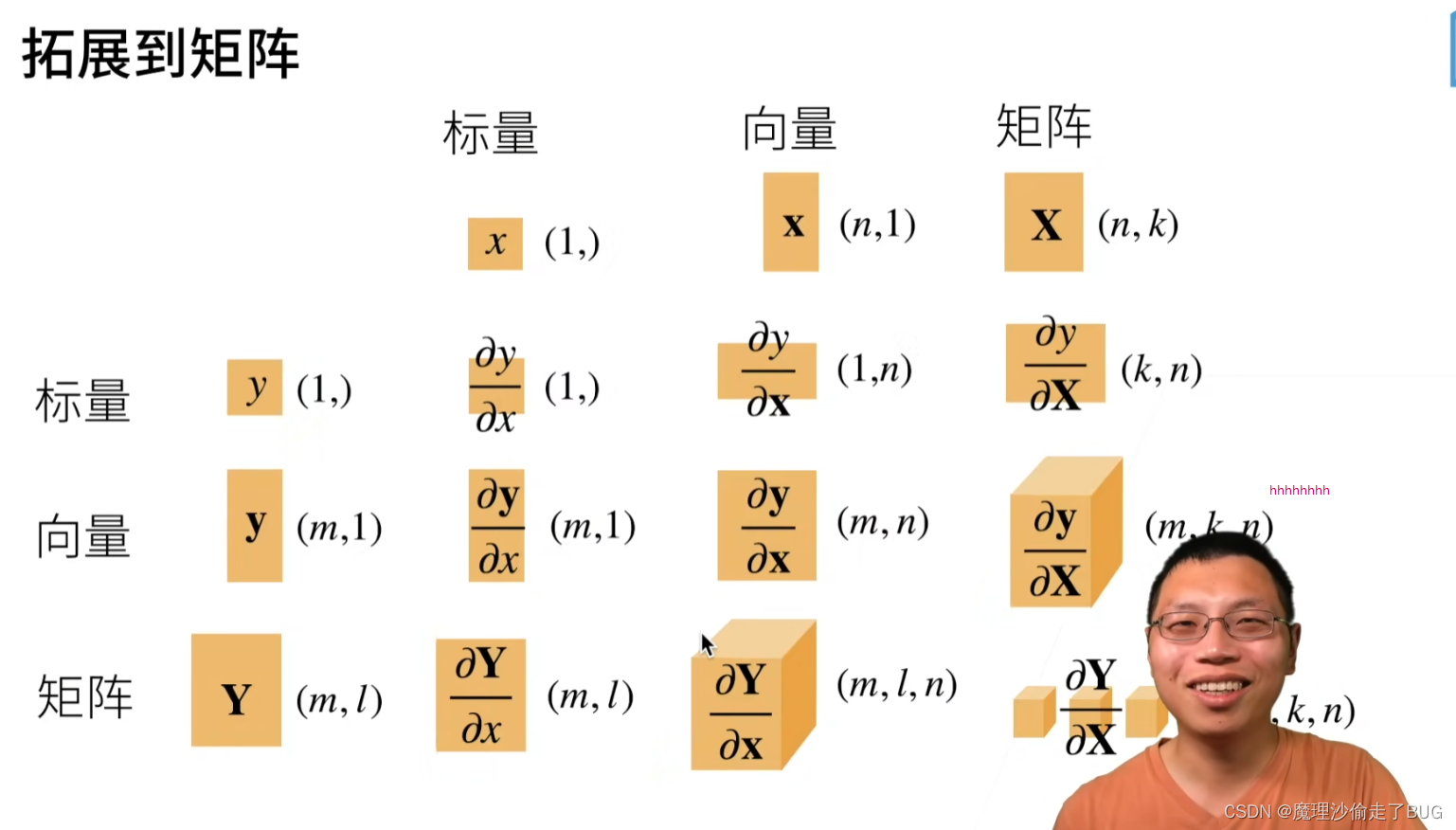
拓展到矩阵
就是升维度,升到了四维空间,矩阵可以相当于四维空间里的向量,反正挺难懂的,我看个乐hhhhhhhh