一、说明
KNN算法是一个分类算法,基本数学模型是距离模型。K-最近邻是一种超级简单的监督学习算法。它可以应用于分类和回归问题。虽然它是在 1950 年代引入的,但今天仍在使用。然而如何实现,本文将给出具体描述。

来源:维基百科
二、KNN原理解释
让我们使用一个简单的 2D 示例来更好地理解。我们有一个包含 3 组的标记数据集。我们的目标是找出给定的新观察属于哪个组。
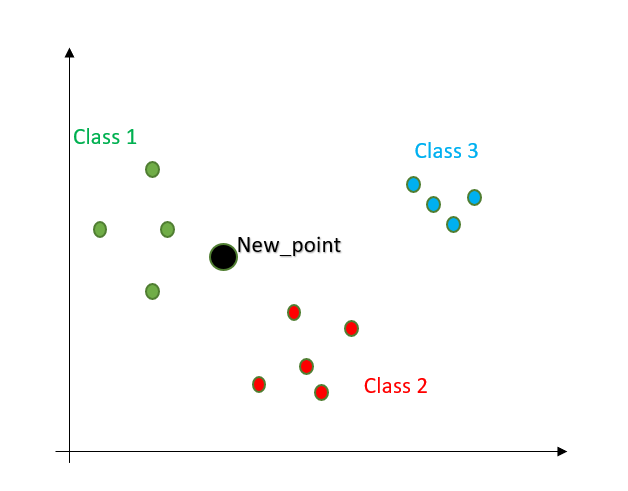
首先,找到给定新点到其他点的距离。
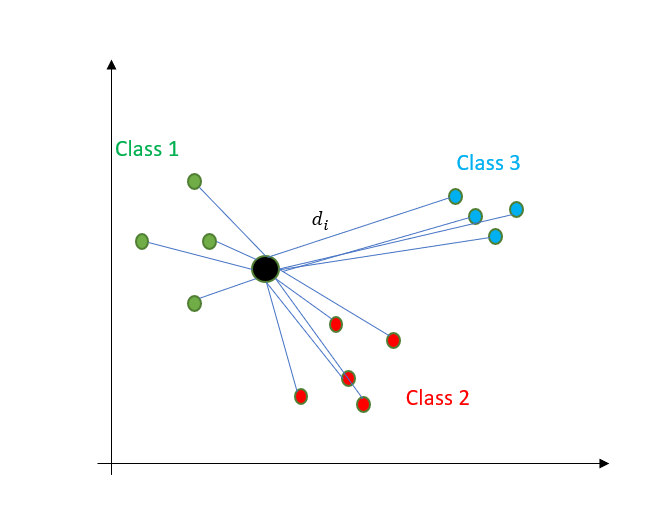
计算距离有不同的方法。最常用的是欧几里得距离和曼哈顿距离。
2.1 欧氏距离
这个你小学就知道了。您在毕达哥拉斯定理中发现的斜边。

Source: Wikipedia

欧氏距离方程
假设 m 维中有 2 个点。将每个维度中两个点的值相互减去,然后将这些值的平方相加。取总值的平方根。
2.2 曼哈顿距离
曼哈顿距离(换句话说,出租车距离)是通过网格计算的。想象一下仅使用道路就能从地图上的一个点到达另一个点。最短路线是曼哈顿距离。鸟瞰距离是欧氏距离。

Source: Wikipedia

曼哈顿距离方程
计算距离后,我们将每个距离从小到大排序。考虑直到所选 k 值的距离数。无论大多数人属于哪一类,那将是我们新点的群体。
在回归问题中,取最接近的 k 个选定点值的平均值。
KNN 算法对异常值和不平衡数据集很敏感。
K值控制过拟合和欠拟合之间的平衡。
-
小K:低偏差,高方差->过度拟合
-
大 K:高偏差、低方差 -> 欠拟合
2.3 Python代码
sklearn实现 我们用 Iris 数据集来演示一下。
from sklearn import datasets
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import confusion_matrix, accuracy_score
iris = datasets.load_iris()
X, y = iris.data, iris.targetX_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1234
) 以上代码(从头开始)
model = Knn()
model.fit(X_train, y_train)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
print("Manual Accuracy:", accuracy(y_test, y_pred))#OUT
[[ 9 0 0]
[ 0 12 1]
[ 0 0 8]]
Manual Accuracy: 0.9666666666666667 sklean训练
model = KNeighborsClassifier(n_neighbors=5)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
print("Manual Accuracy:", accuracy(y_test, y_pred))#OUT
[[ 9 0 0]
[ 0 12 1]
[ 0 0 8]]
Manual Accuracy: 0.9666666666666667 三、如何选择正确的 K 值
尝试不同的值来选择正确的k值,并根据误差选择最佳的k值。未选择始终给出最小误差的 k 值。这可能会导致过度拟合。遵循所谓的肘击战术。在改善减少的 k 值处,停在那里并选择相应的 k 值。
k_list = list(range(1,50,2))
cv_scores = []for k in k_list:
knn = KNeighborsClassifier(n_neighbors=k)
scores = cross_val_score(knn, X_train, y_train, cv=10, scoring='accuracy')
cv_scores.append(scores.mean())MSE = [1 - x for x in cv_scores]plt.figure()
plt.figure(figsize=(15,10))
plt.title('K vs Error', fontsize=20, fontweight='bold')
plt.xlabel('K', fontsize=15)
plt.ylabel('Error', fontsize=15)
sns.set_style("whitegrid")
plt.plot(k_list, MSE)plt.show() 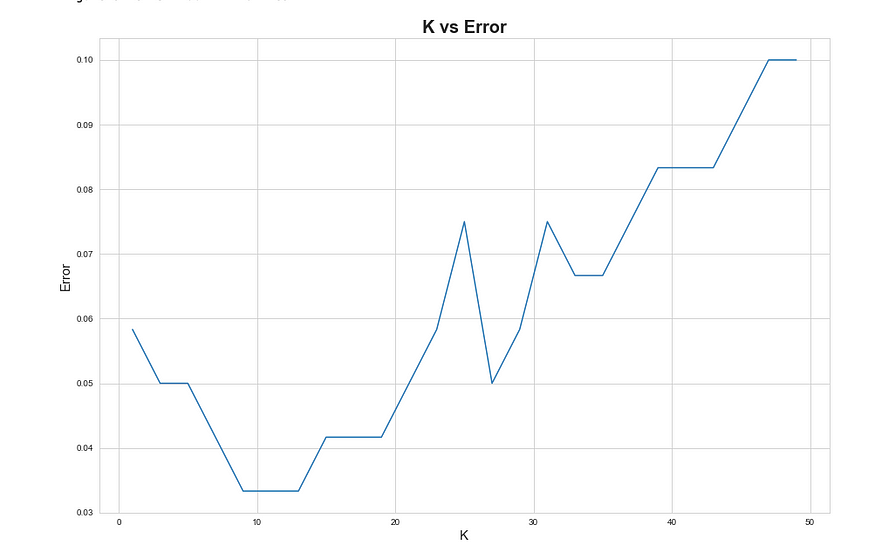
K 与误差图表。我们可以选择 k 作为 9。