1. 斐波那契数列
1,1,2,3,5,8,13,..... f(n) = f(n-1) + f(n-2)
代码实现
public static int count_2 = 0;
public int fibonacci(int n){
if (n <= 2){
count_2++;
return n;
}
int f1 = 1;
int f2 = 2;
int sum = 0;
for (int i = 3; i < n; i++) {
count_2++;
sum = f1 + f2;
f1 = f2;
f2 = sum;
}
return sum;
}当n=20时,count是21891次,当n=30的时候结果是2692537,接近270万,为什么这么高,因为里面存在大量的循环,下面图中,n=8时,f(6)就重复计算两次,很多结点会被重复计算。
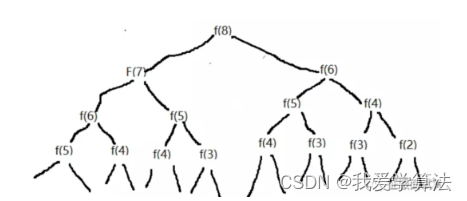
如何将其优化减少重复计算,这也是下面推导动态规划需要考虑的,可以将计算结果保存到数组中,f(n)的值保存在数组中,f(n)=arr[n],某个位置已经被计算出来,下次需要的时候直接取出来,不需要再递归。
public static int[] arr = new int[50];
public static int count_3 = 0;
public static void main(String[] args) {
Arrays.fill(arr,-1);
arr[0] = 1;
System.out.println(fibonacci(31));
}
static int fibonacci(int n){
if (n == 2 || n == 1){
count_3++;
arr[n] = n;
return n;
}
if (arr[n] != -1){
count_3++;
return arr[n];
}else {
count_3++;
arr[n] = fibonacci(n - 1) + fibonacci(n - 2);
return arr[n];
}
}2 路径连环炮
文中的动态规划我们简称DP,路径相关的问题来分析动态规划,路径问题易于画图,方便理解,循序渐进的理解DP
2.1 第一炮:基本问题统计路径总数
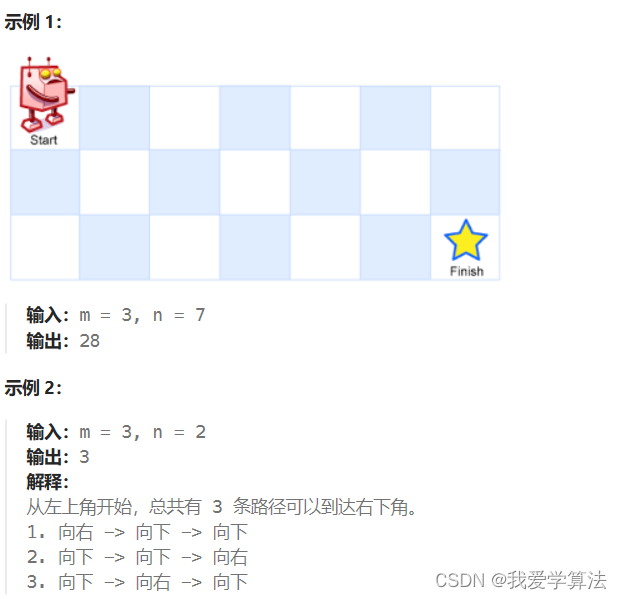
LeetCode62 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
第一炮,我们研究如何通过递归来解决此问题,如下图所示,从起点开始要么向右,要么向下,每一种否会导致剩下的区间减少了一列或一行,形成两个不同区间的过程,每个区间继续以红点为起点继续上述操作,所以这就是一个递归的过程,

从图中寻找规律,目标从起点到终点,只能向右或向下,
1. 向右走一步,起点下面灰色的不会再被访问,后面剩一个3X1的矩阵,只能一直往下走,只有一种路径,
2. 向下走一步,起点右侧不不能再被访问,剩一个2X2的矩阵,还剩两种路径,
这是3X2的矩阵,一共有3中路径,一个2X2的矩阵和3X1的矩阵路径之和。
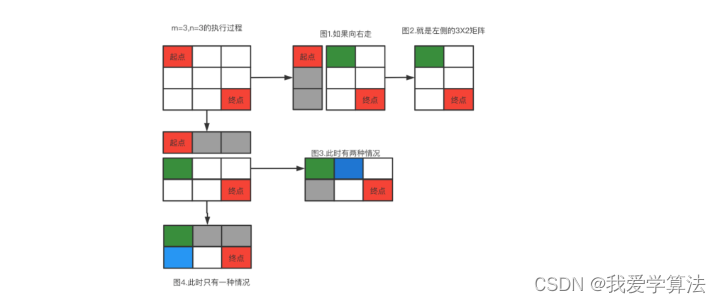
同样我们推导一个3X3的矩阵,就是一个3X2的矩阵和2X3的路径之和,
所以,对于一个mxn的矩阵,求路径的方法是serch(m,n)=search(m-1,n)+search(m,n-1);
public int uniquePath(int m,int n){
return search(m,n);
}
private int search(int m, int n) {
if (m == 1 || n == 1){
return 1;
}
return search(m-1,n) + search(m,n-1);
}对于3X3的矩阵,我们可以用二叉树表示
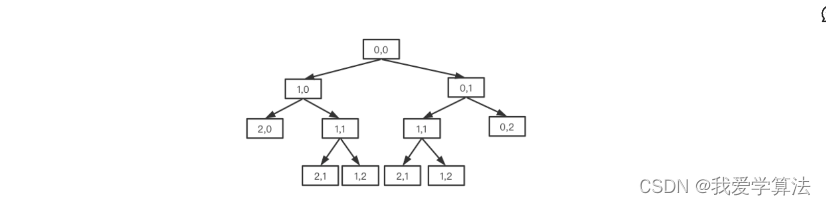
我们可以发现,和文章开头我们提到的一样,中间有重复计算,1,1计算了两次,那么如何优化
2.2 第二炮:使用二维数组优化递归
我们知道上面出现了重复计算,{1,1}出现两次,在{1,1}位置处,不管是从{0,1}还是{1,0}到来,都会产生两种走法,我们可以用二维数组记忆化搜索就不用两次遍历了,

每个格子都表示从起点开始到当前的位置有几种方式,这样我们通过计算路径的时候可以先查下二维数组有没有记录,有就直接读,没有再计算,这样就可以避免大量的重复计算,这就是记忆化搜索。
从上面的分析我们得到两个规律:
1.第一行和第一列都是1.
2.其他格子的值都是其左侧和上方格子之和,对于mXn的格子都适应。
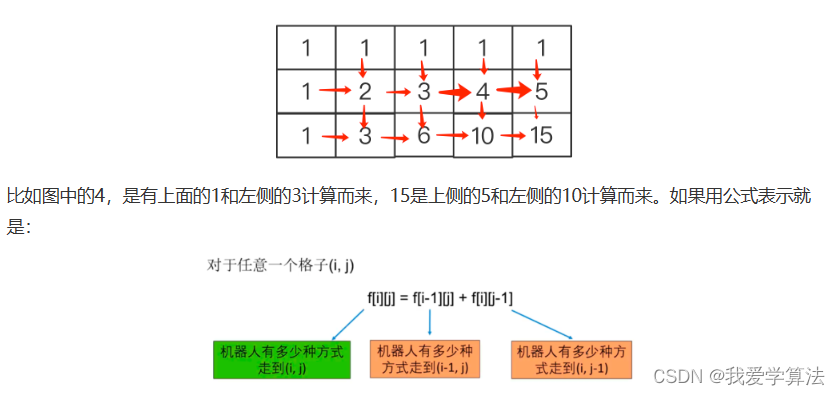
public int uniquePath(int m, int n){
int[][] f = new int[m][n];
f[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i > 0 && j > 0){
f[i][j] = f[i -1][j] + f[i][j -1];
}else if (i > 0){
f[i][j] = f[i -1][j];
} else if (j > 0) {
f[i][j] = f[i][j -1];
}
}
}
return f[m -1][n -1];
}2.3 第三炮:滚动数组:用一维代替二维数组
第三炮,我们通过滚动数组来优化此问题,上面缓存空间使用二维数组,占据空间大,能否进一步优化,我们看上面的二维数组找出规律。
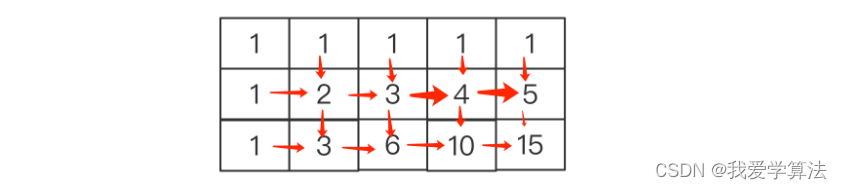
发现除了第一行和第一列都是1外,每个位置都是其左侧和上方的格子之和,可以用一个大小为n的一维数组来解决:
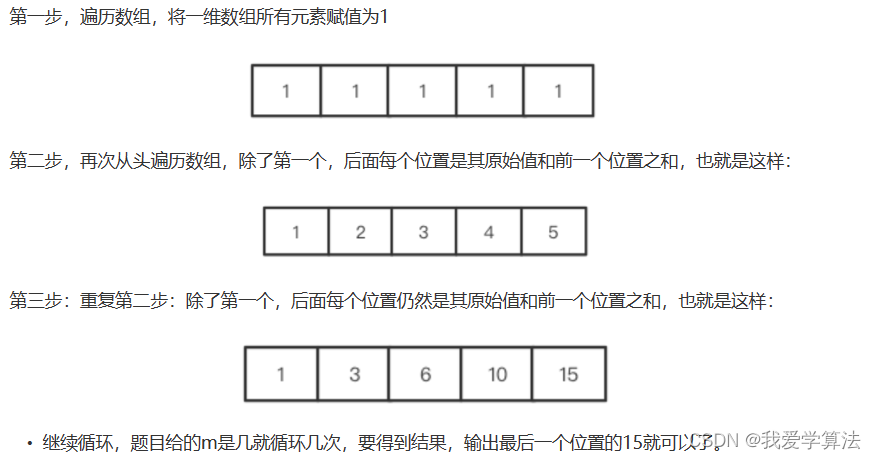
将几个一维数组拼接起来,就是和上面的二维数组完全一样的,反复更新数组的策略就是滚动数组,计算公式是:dp[j] = dp[j]+dp[j-1]
public int uniquePaths(int m, int n){
int[] dp = new int[n];
//将数组初始元素初始为1
Arrays.fill(dp,1);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
//等式左边的dp[j]是上一次计算后的,再加上左边的dp[j-1]即为当前结果
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n -1];
}这个题目包含了DP(动态规划)里的多个方面,比如重复子问题、记忆化搜索、滚动数组等等,这就是最简单的动态规划了,只不过我们这里的规划是dp[j] = dp[j] + dp[j -1] ;不用进行复杂的比较和计算。
3. 理解动态规划
DP一般是让我们找最值的,例如最长公共子序列,最关键的是DP问题的子问题不是相互独立的,如果递归直接分解会导致重复计算指数级增长,开头的热身题,而DP的最大价值是为了消除冗余,加速计算。
动态规划解决什么问题:A求有多少种走法,B输出所有的走法
动态规划计算效率高,但是不能找到满足要求的路径,
区分动态规划和递归最重要的一条是:动态规划只关心当前结果是什么,怎么来的就不管了,所以动态规划无法获得完整的路径,这与回溯不一样,回溯能够获得一条甚至所有满足要求的完整路径。
DP的基本思想是将待求解问题分解成若干个子问题,先求子问题,再从这些子问题中得到原问题的解,既然要找最值,那么必然要做的就是穷举来找所有的可能,然后选择“最”的那个,这就是为什么再DP代码中大量判断逻辑都会被套上min()或者max(),
既然穷举,那为什么还有DP的概念?这是因为穷举的过程中存在大量的重复计算,效率低下,所以我们要使用记忆化搜索等方式来消除不必要的计算,所谓记忆化搜索就是将已经计算好的结果先存在数组里面,后面就直接读就不再重复计算了,
既然记忆化能解决问题,为啥DP这么难,因为DP问题一定具备“最优子结构”,这样才能让记忆时得到准确结果,至于什么时最优子结构,后面还有具体问题,
有了最优子结构,还要正确的“状态转移方程”,才能正确的穷举,也就是递归关系,大部分递归都可以通过数组实现,因此代码结构一般是这样的for循环,这就是DP的基本模板:
//初始化base case ,也就是刚开始的几种场景,有几种枚举
dp[0][0][...] = base case
//进行状态转移
for 状态1 状态1的所有取值
for 状态2 in 状态2的所有取值
dp[状态1][状态2] = 求最值Max(选择1,选择2,...)
动态规划题目有三种基本类型:
1. 计数有关,例如求多少种方式到右下角,有多少种方式选出K个数是使得什么什么的问题,不关心路径是什么
2. 求最大值最小值,最多最少等,例如最大数字和,最长上升子序列,最长公共子序列,最长回文序列等
3. 求存在性,例如取石子游戏,先手是否必胜,能不能选出k个数使得什么什么等等
不管那种解决问题的模板也是类似的
- 第一步:确定状态和子问题,也就是枚举出某个位置所有的可能性,对于DP,大部分题目分析最后一步更容易一些,得到递推关系,同时将问题转换为子问题。
- 第二步:确定状态转移方程,也就是数组要存储什么内容,很多时候状态确定之后,状态转移方程也就确定了,前两步也可作为为第一步骤
- 第三步:确定初始和边界条件情况,注意细心,尽量周全
- 第四步:按照从小到大的顺序计算:f[0],f[1],f[2]
我们自始至终,都要在大脑里装一个数组(可能是一维,也可能是二维),要看这个数组每个元素的含义是什么(也就是状态),要看每个数组是根据谁来算的(状态转移方程),然后就是从小到大挨着将数组填满(从小到大计算,实现记忆化搜索),最后看那个位置是我们想要的结果。