目录
前言
思维导图
一.树
树的定义
二.二叉树
1.二叉树的定义
2.二叉树的形态(图)
3.二叉树的性质
三.满二叉树
1.定义
2.特点和性质
四.完全二叉树
1.定义
2.特点和性质
前言
今天开始我们就学习新的数据结构类型啦!没错它就是大名鼎鼎的树状结构,其实在学习数据结构之前或者在学习C语言的时候我们都听说过树和二叉树,但是我们却没有去深入探讨过这种数据结构类型的相关性质和方法,我个人也是一样的,那从现在开始我们就开始去正式学习这种新的数据结构类型吧!
思维导图
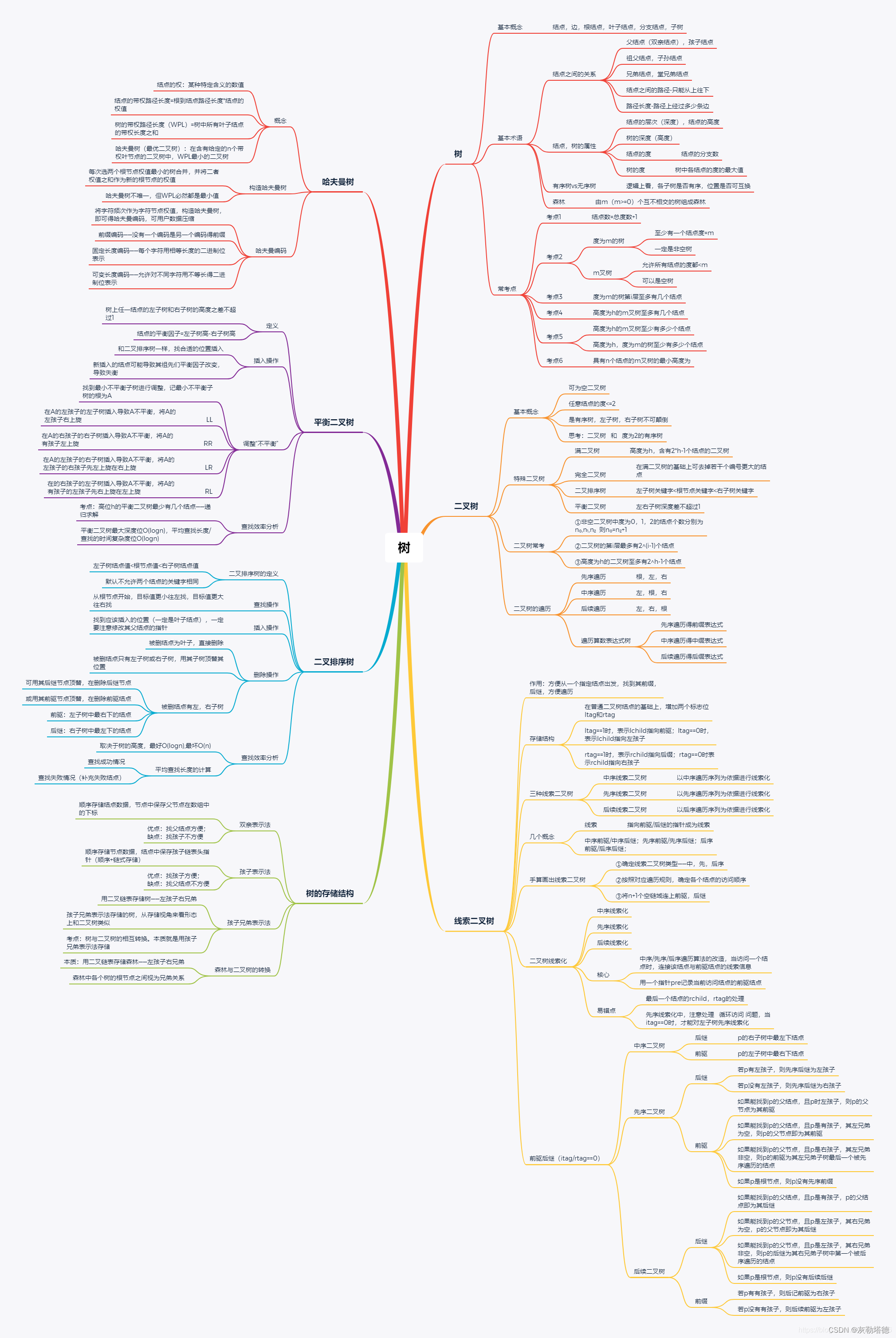
一.树
树的定义
简介
树是一种数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个节点有零个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树。
定义
树(tree)是包含 n(n≥0) [2] 个节点,当 n=0 时,称为空树,非空树中
条边的有穷集,在非空树中:
(1)每个元素称为节点(node)。
(2)有一个特定的节点被称为根节点或树根(root)。
(3)除根节点之外的其余数据元素被分为多个互不相交的集合
空集合也是树,称为空树。空树中没有节点;
1.孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
2.节点的度:一个节点含有的子节点的个数称为该节点的度;
3.叶节点或终端节点:度为0的节点称为叶节点;
4.非终端节点或分支节点:度不为0的节点;
5.双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
6.兄弟节点:具有相同父节点的节点互称为兄弟节点;
7.树的度:一棵树中,最大的节点的度称为树的度;
8.节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
9.树的高度或深度:树中节点的最大层次;
10.堂兄弟节点:双亲在同一层的节点互为堂兄弟;
11.节点的祖先:从根到该节点所经分支上的所有节点;
12.子孙:以某节点为根的子树中任一节点都称为该节点的子孙;
13.有序树:树中的节点各子树从左到右是有次序的
14.森林:由多棵互不相交的树的集合称为森林
示意图: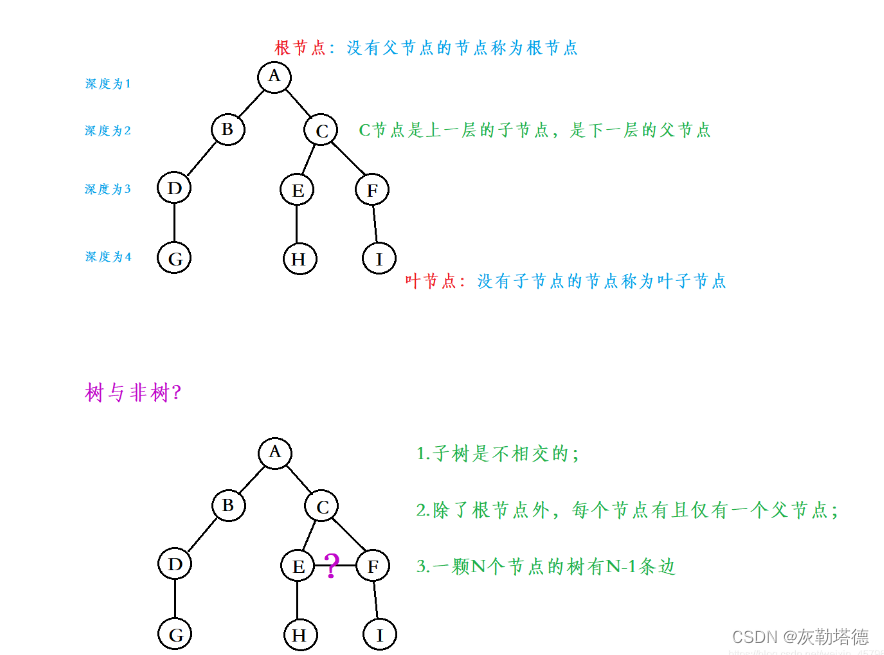
二.二叉树
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分 。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点
1.二叉树的定义
定义:二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树 。
1、每个结点最多有俩孩子(二叉树中不存在度大于 2 的结点)
2、子树有左右之分,其次序不能颠倒。
3、二又树可以是空集合,根可以有空的左子树或空的右子树。
注意:
1.二叉树不是树的特殊情况,它们是两个概念又树结点的子树要区分左子树和右子树,即使只有一棵子树也要进行区分,说明它是左子树,还是右子树
2.树当结点只有一个孩子时,就无须区分它是左还是右的次序。因此二者是不同的。这是二叉树与树的最主要的差别。
3.具有两个结点的树只有一种状态具有两个结点的二叉树有两种状态(也就是二又树每个结点位置或者说次序都是固定的,可以是空,但是不可以说它没有位置,而树的结点位置是相对于别的结点来说的,没有别的结点时,它就无所谓左右了)
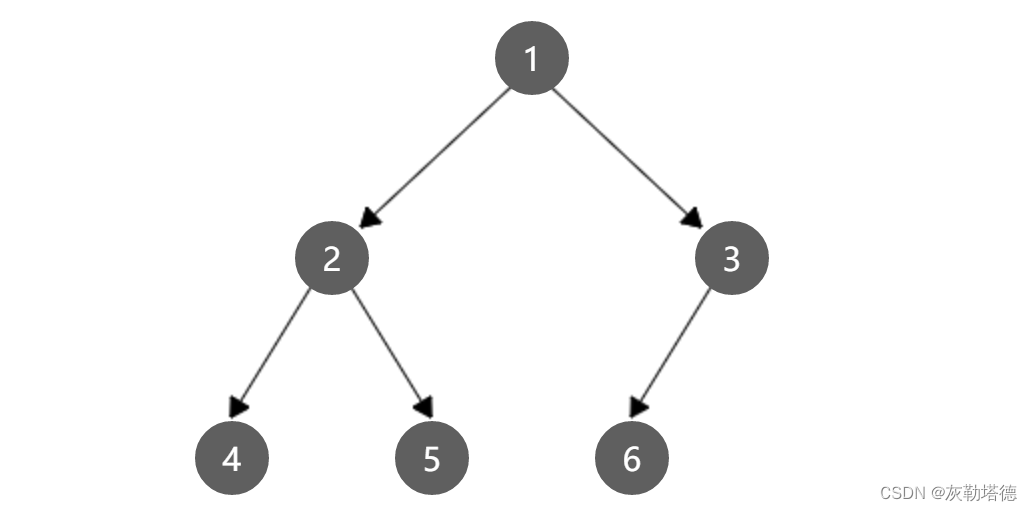
2.二叉树的形态(图)
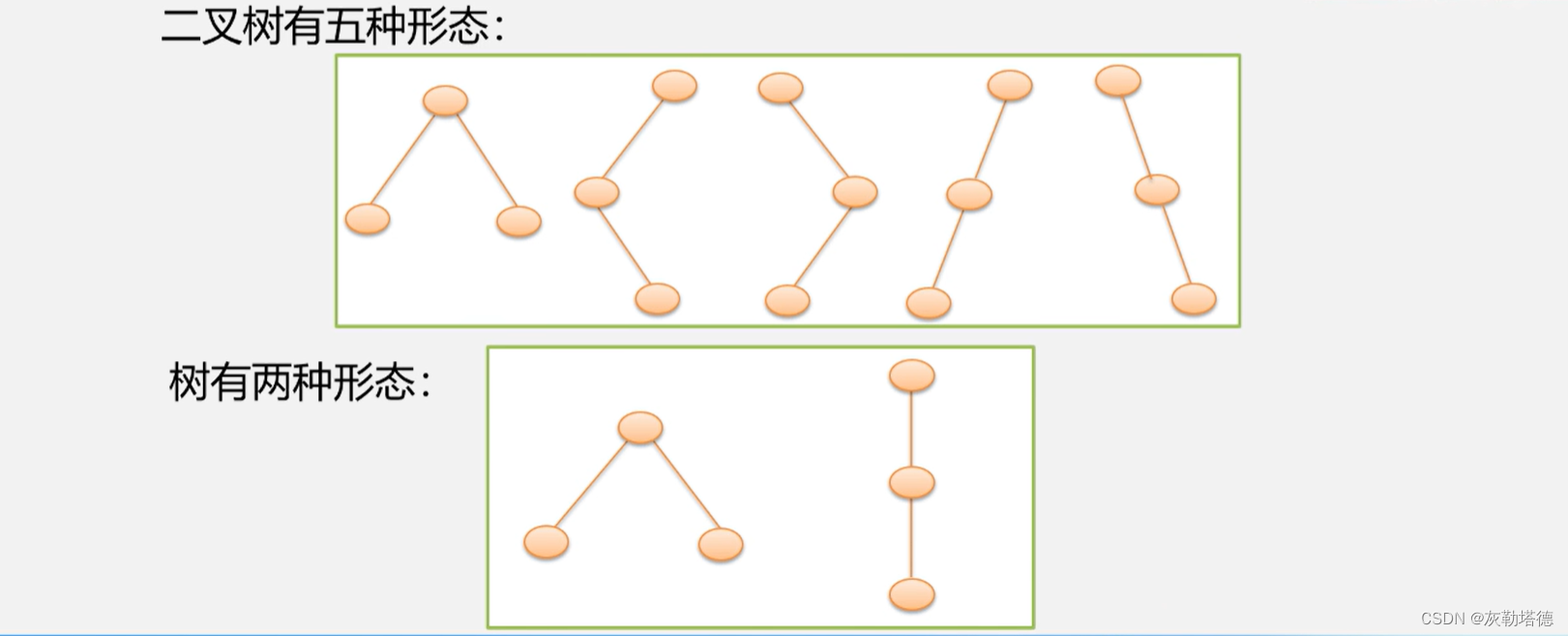
3.二叉树的性质
性质1:二叉树的第i层,至多有 2^(i-1) 个节点(i>=1),最少有1个节点
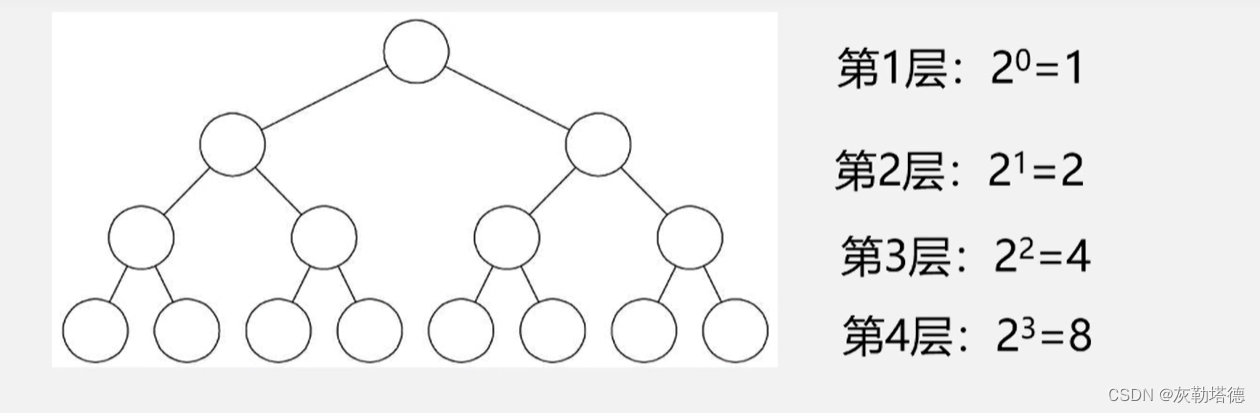
性质2:一个深度为k的二叉树,最多一共有2^k-1个节点(k>=1),至少有k个节点

性质3:对任何一棵二叉树 T 如果其叶子数为 n0,度为2的结点数为 n2,则 n0 = n2 + 1
证明过程如下:
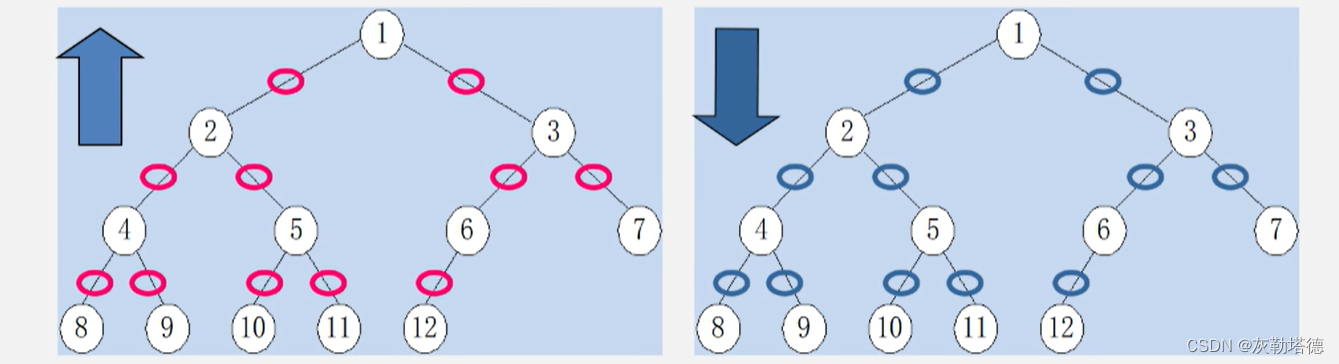
分两种情况,首先从下往上看,总边数为B,总节点数为n,那么我们就可以得到 B=n-1;然后从上往下看,度数为2的节点数为n2,度数为1的节点数为n1,那么 B=2*n2+n1
B=n-1=2*n2+n1
n=n1+n2+n0
联立课解得: n0=n2+1
三.满二叉树
1.定义
如果一个深度为k的二叉树,其所有的节点总数为2^k-1,那么这个二叉树就是满二叉树
如图所示: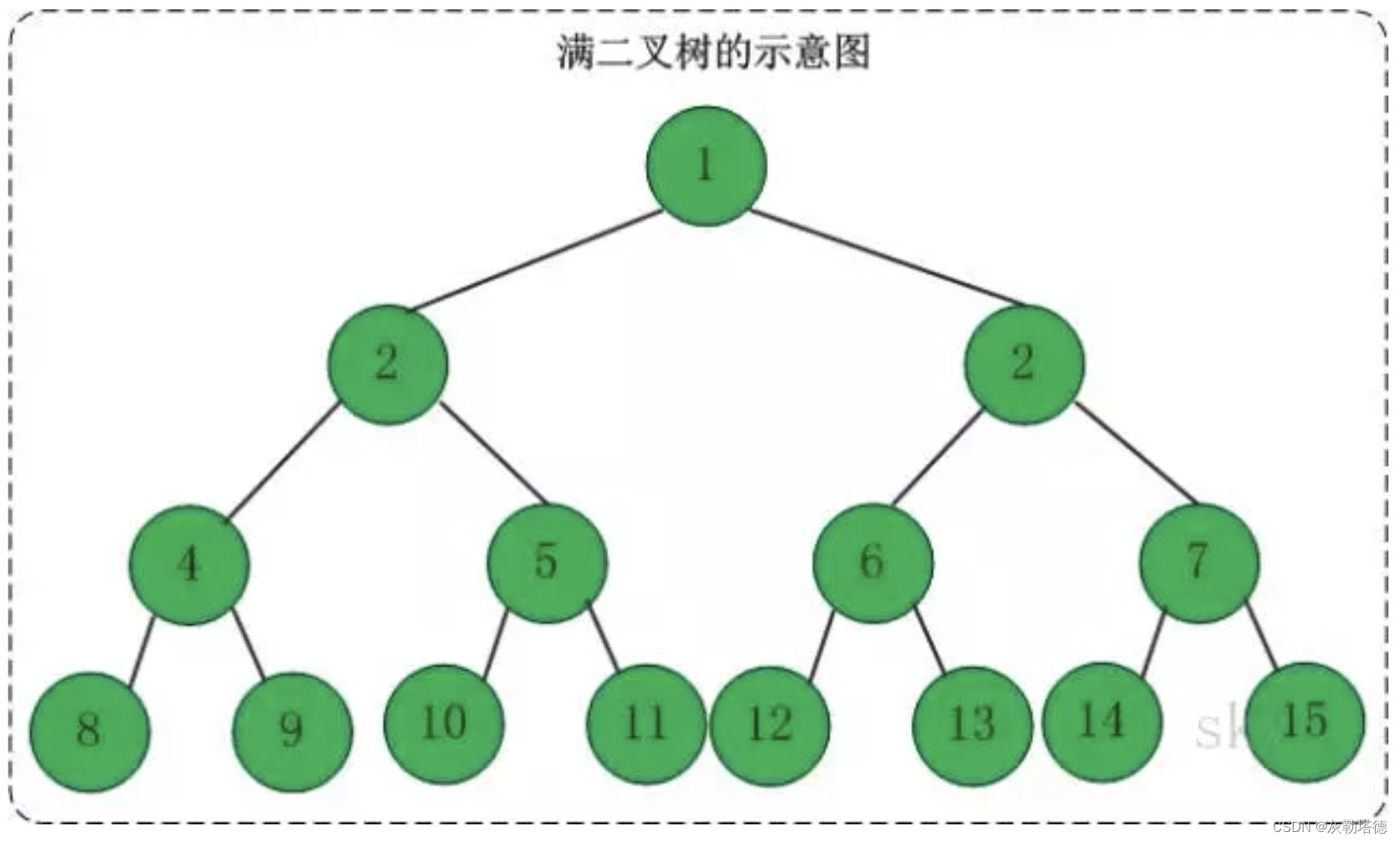
2.特点和性质
特点:
1.每一层上的结点数都是最大结点数 (即每层都满)
2.叶子节点全部在最底层
对满二叉树结点位置进行编号编号规则:
1.从根结点开始,自上而下,自左而右。
2.每一结点位置都有元素
四.完全二叉树
1.定义
当且仅当其每一个结点都与深深度为k的具有n个结点的二又树,度为k的满二又树中编号为 1~n 的结点一- 对应时,称之为完全叉树。
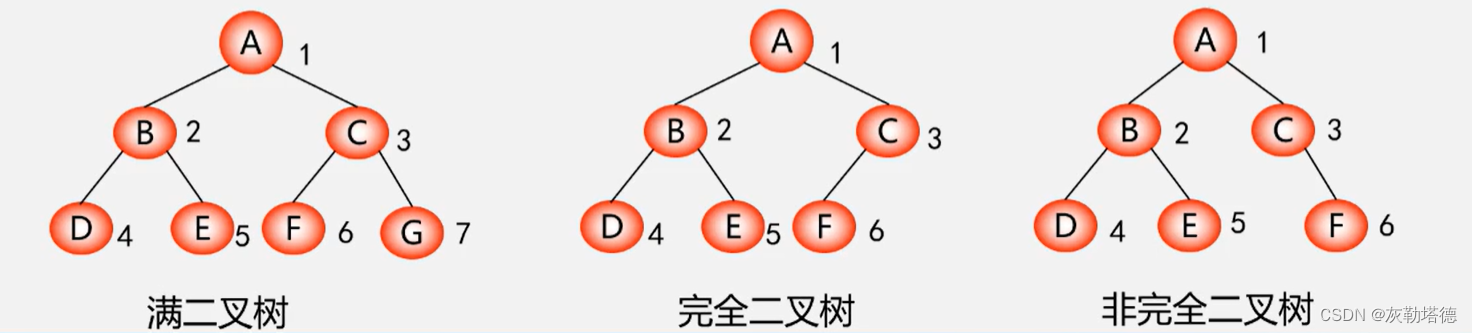
注意:
满二叉树是一个完全二叉树,但是完全二叉树不一定是满二叉树。如果满二叉树从最后一个节点开始连续去掉任意一个节点那就是一个完全二叉树(一定是连续去掉的!)
2.特点和性质
特点:
1.叶子只可能分布在层次最大的两层上
2.对任一结点,如果其右子树的最天层次为i.则其左子树的最大层次必为i或i+ 13.具有n个节点的完全二叉树,其深度为log2n+1
以上就是本期的全部内容了,我们下一期继续学习二叉树的其他内容,下次见!
分享一张壁纸: