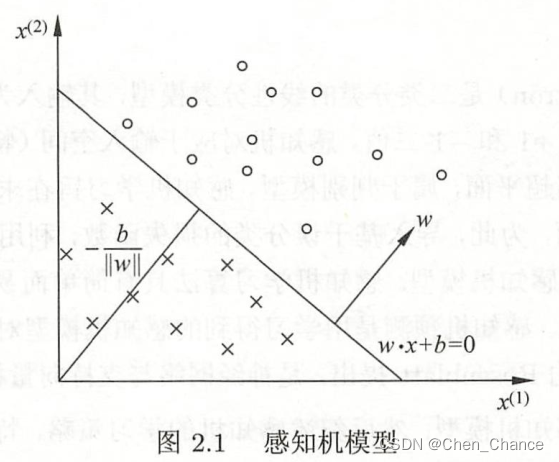
感知机(perceptron)时二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面
想象一下在一个平面上有一些红点和蓝点,这些点代表不同的类别。分离超平面就是一条线,可以将红点和蓝点分开,使得所有的红点都在一侧,而蓝点都在另一侧。这条线(或者平面,对于高维数据)被称为分离超平面。
2.1感知机模型
定义2.1(感知机):假设输入空间(特征空间)是
X
⊆
R
n
X \subseteq R^n
X⊆Rn,输出空间是
Y
=
{
+
1
,
−
1
}
Y=\{+1,-1\}
Y={+1,−1}。输入
x
∈
X
x \in X
x∈X表示实例的特征向量,对应于输入空间(特征空间)的点;输出
y
∈
Y
y \in Y
y∈Y表示实例的类别。由输入空间到输出空间的如下函数:
f
(
x
)
=
s
i
g
n
(
w
⋅
x
+
b
)
f(x)=sign(w \cdot x+b)
f(x)=sign(w⋅x+b)
称为感知机。其中,w和b为感知机模型参数,
w
∈
R
n
w \in R^n
w∈Rn叫做权重(weight)或权重向量(weight vector),
b
∈
R
b \in R
b∈R叫做偏置(bias),
w
⋅
x
w \cdot x
w⋅x表示w和x的内积。sign是符号函数,即
s
i
g
n
(
x
)
=
{
+
1
x
≥
0
−
1
x
<
0
sign(x)=\begin{cases} +1 & x≥0 \\ -1 & x<0 \\ \end{cases}
sign(x)={+1−1x≥0x<0
内积是线性代数中的一个概念,也被称为点积或标量积。它是两个向量之间的一种运算,将两个向量相乘并得到一个标量(实数)的结果。内积通常用于衡量向量之间的相似性、角度和投影等性质。
内积的一般定义是:
对于两个实数向量 a 和 b,它们的内积(点积)表示为 a·b,计算方式如下:
a·b = |a| * |b| * cos(θ)
以下是一个简单的例子来说明内积的概念:
假设有两个二维向量 a 和 b,它们分别表示为:
a = [2, 3]
b = [4, 1]
要计算 a 和 b 的内积,首先需要计算它们的长度(模):
|a| = √(2^2 + 3^2) = √(4 + 9) = √13
|b| = √(4^2 + 1^2) = √(16 + 1) = √17
接下来,计算 a 和 b 之间的夹角 θ,可以使用余弦公式:
cos(θ) = (a·b) / (|a| * |b|)
将 a 和 b 的值代入:
cos(θ) = (2 * 4 + 3 * 1) / (√13 * √17) = (8 + 3) / (√13 * √17) = 11 / (√13 * √17)
现在,我们可以计算内积 a·b:
a·b = |a| * |b| * cos(θ) = √13 * √17 * (11 / (√13 * √17)) = 11
所以,向量 a 和 b 的内积是 11。
内积的计算可以帮助我们理解向量之间的相对方向以及它们之间的相似性。在许多应用中,内积是一个重要的数学工具,例如在机器学习中用于计算特征之间的相关性,以及在物理学中用于计算力学和电磁学中的各种问题。
感知机模型的参数包括权重(weight)向量 w ∈ R n w \in \mathbb{R}^n w∈Rn 和偏置(bias) b ∈ R b \in \mathbb{R} b∈R,这两个参数的维度之所以不同,是因为它们的作用和数学表达的需要不同。
- 权重向量 w ∈ R n w \in \mathbb{R}^n w∈Rn:
- 权重向量 w w w 的维度为 n n n,其中 n n n 表示输入特征的数量。每个特征都有一个对应的权重,用于衡量该特征对模型的重要性。权重向量中的每个元素 w i w_i wi 对应于一个特征,表示该特征在模型中的权重。每个特征都有一个权重,因此需要 n n n 个权重值。
- 偏置 b ∈ R b \in \mathbb{R} b∈R:
- 偏置 b b b 是一个标量(单个实数),它不依赖于特征的数量。偏置的作用是在计算模型的输出时引入一个偏移量,用于调整模型的预测值。它可以理解为模型在没有任何特征输入时的输出值,相当于截距或偏移项。
考虑一个简单的情况,比如二元分类问题,输入特征有 n n n 个,感知机模型的输出是根据权重向量 w w w 对输入特征加权求和后再加上偏置 b b b,然后通过 sign 函数进行分类决策。这就是为什么需要一个长度为 n n n 的权重向量 w w w 和一个标量偏置 b b b 的原因。
总之,权重向量 w w w 的维度与输入特征的数量相关,而偏置 b b b 是一个标量,不依赖于特征的数量,它们一起组成了感知机模型的参数,用于对输入进行线性加权和分类决策。
2.2感知机学习策略
2.2.1数据集的线性可分性
定义2.2(数据集的线性可分性)
2.2.2感知机学习策略
2.3感知机学习算法
2.3.1感知机学习算法的原始形式
∇ w L ( w , b ) = ∑ x i ∈ M y i x i \nabla_wL(w,b)=\sum\limits_{x_i \in M}y_i x_i ∇wL(w,b)=xi∈M∑yixi