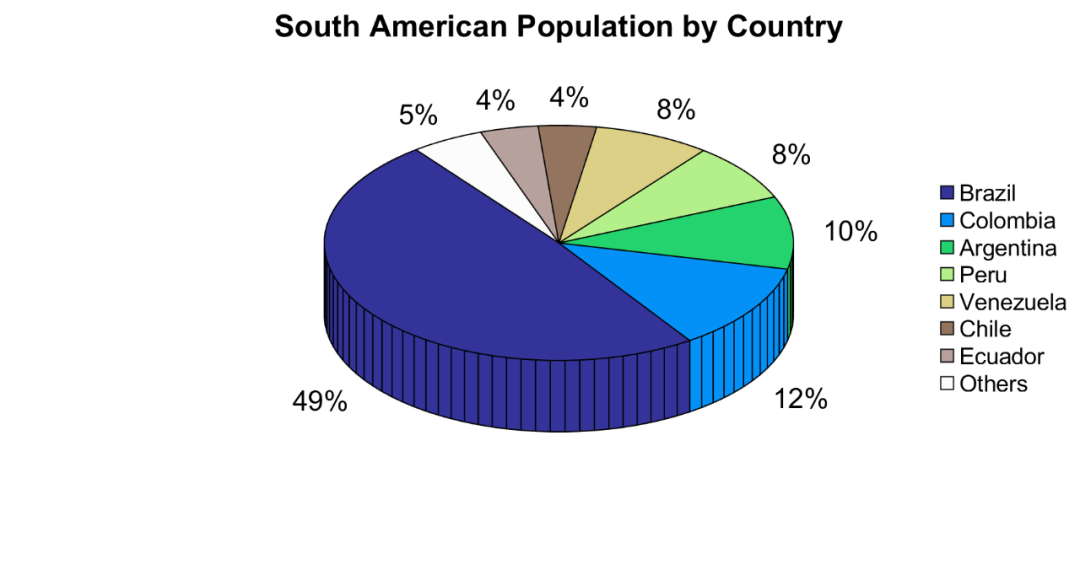
贝塞尔和二次方曲线
贝塞尔曲线可以是二次和三次方的形式，常用于绘制复杂而有规律的形状。
绘制贝塞尔曲线主要使用bezierCurveTo方法。该方法可以说是lineTo的曲线版，将从当前坐标点到指定坐标点中间的贝塞尔曲线追加到路径中。该方法的定义如下。
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
该方法使用6个参数。绘制贝塞尔曲线的时候，需要两个控制点，cp1x为第一个控制点的横坐标，cp1y为第一个控制点的纵坐标；cp2x为第二个控制点的横坐标，cp2y为第二个控制点的纵坐标；x为贝塞尔曲线的终点横坐标，y为贝塞尔曲线的终点纵坐标。
绘制二次样条曲线，使用的方法是quadraticCurveTo。该方法的定义如下。
quadraticCurveTo(cp1x, cp1y, x, y)
两种方法的区别如图17.8所示。它们都是一个起点一个终点（图中的蓝点），但二次方贝塞尔曲线只有一个（红色）控制点，而三次方贝塞尔曲线有两个。
参数x和y是终点坐标，cp1x和cp1y是第一个控制点的坐标，cp2x和cp2y是第二个控制点的坐标。
【例17.5】下面看一下使用bezierCurveTo方法的实例。本例中使用bezierCurveTo方法绘制一个红色实心的红心。
实现的主要代码如下。
context.beginPath();
context.fillStyle = '#c00';
context.strokeStyle = '#c00';
context.moveTo(75,40);
context.bezierCurveTo(75,37,70,25,50,25);
context.bezierCurveTo(20,25,20,62.5,20,62.5);
context.bezierCurveTo(20,80,40,102,75,120);
context.bezierCurveTo(110,102,130,80,130,62.5);
context.bezierCurveTo(130,62.5,130,25,100,25);
context.bezierCurveTo(85,25,75,37,75,40);
context.fill();
context.stroke();
从上面的代码可以看出，红心的绘制主要是多次使用了三次方贝塞尔曲线绘制的。
【例17.6】下面再来看一下使用quadraticCurveTo方法绘制二次方线的实例。本例主要是绘制了一个用于解释说明的对话框。其实现的主要代码如下。
context.beginPath();
context.moveTo(75,25);
context.strokeStyle = '#c00';
context.quadraticCurveTo(25,25,25,62.5);
context.quadraticCurveTo(25,100,50,100);
context.quadraticCurveTo(50,120,30,125);
context.quadraticCurveTo(60,120,65,100);
context.quadraticCurveTo(125,100,125,62.5);
context.quadraticCurveTo(125,25,75,25);
context.stroke();
context.fill();
本例在浏览器中实现的效果。
相对来说，二次样条曲线的绘制比贝塞尔曲线的绘制容易一些，因为绘制贝塞尔曲线时需要两个控制点，而绘制二次样条曲线时只需要一个控制点。因此，quadraticCurveTo方法只需要4个参数就可以了，分别是控制点的横坐标、控制点的纵坐标、二次样条曲线终点的横坐标、二次样条曲线终点的纵坐标。
https://www.bilibili.com/video/BV1Gv4y1Q7px/?p=2&spm_id_from=pageDriver&vd_source=a7816e3b2a3a67ac39dc87f6bf92421c
https://www.bilibili.com/video/BV1Gv4y1Q7px/?p=2&spm_id_from=pageDriver&vd_source=a7816e3b2a3a67ac39dc87f6bf92421c
