Java——B-树

news2025/2/5 20:03:37

概念

当我们使用avl树或者红黑树进行数据检索时，虽然树是平衡的，可以保证搜索的效率大概是logN。但是当我们的数据量比较大时，只能在内存中存储数据在硬盘中的指针，这时如果我们要检索数据，最少也需要比较树的高度次。

解决这个问题一方面需要提高io速度，另一方面就是降低树的高度

而要想降低树的高度，就需要让树叉变多，而我们的B-树，就是一颗M阶的树（M>2），其满足如下性质

性质

  1. 根节点至少有两个孩子
  2. 非根节点至少有M/2-1个关键字，最多M-1个关键字，并且以升序排列
  3. 非根节点至少有M/2个孩子，最多有M个孩子
  4. 关键字key[i]和key[I+1]之间的孩子的值介于两者之间
  5. 所有的叶子节点都在同一层

也就是说，B-树把所有的数据都存储到叶子上，通过关键字来检索数据，这样就可以减少数据的对比，而只用关键字对比即可

插入过程

简单来说就是当一个节点的数据满了，就需要将其右半边的数据拷贝到新的孩子节点里，把最中间的一个数据拷贝到父亲节点

下面通过图画来演示一下
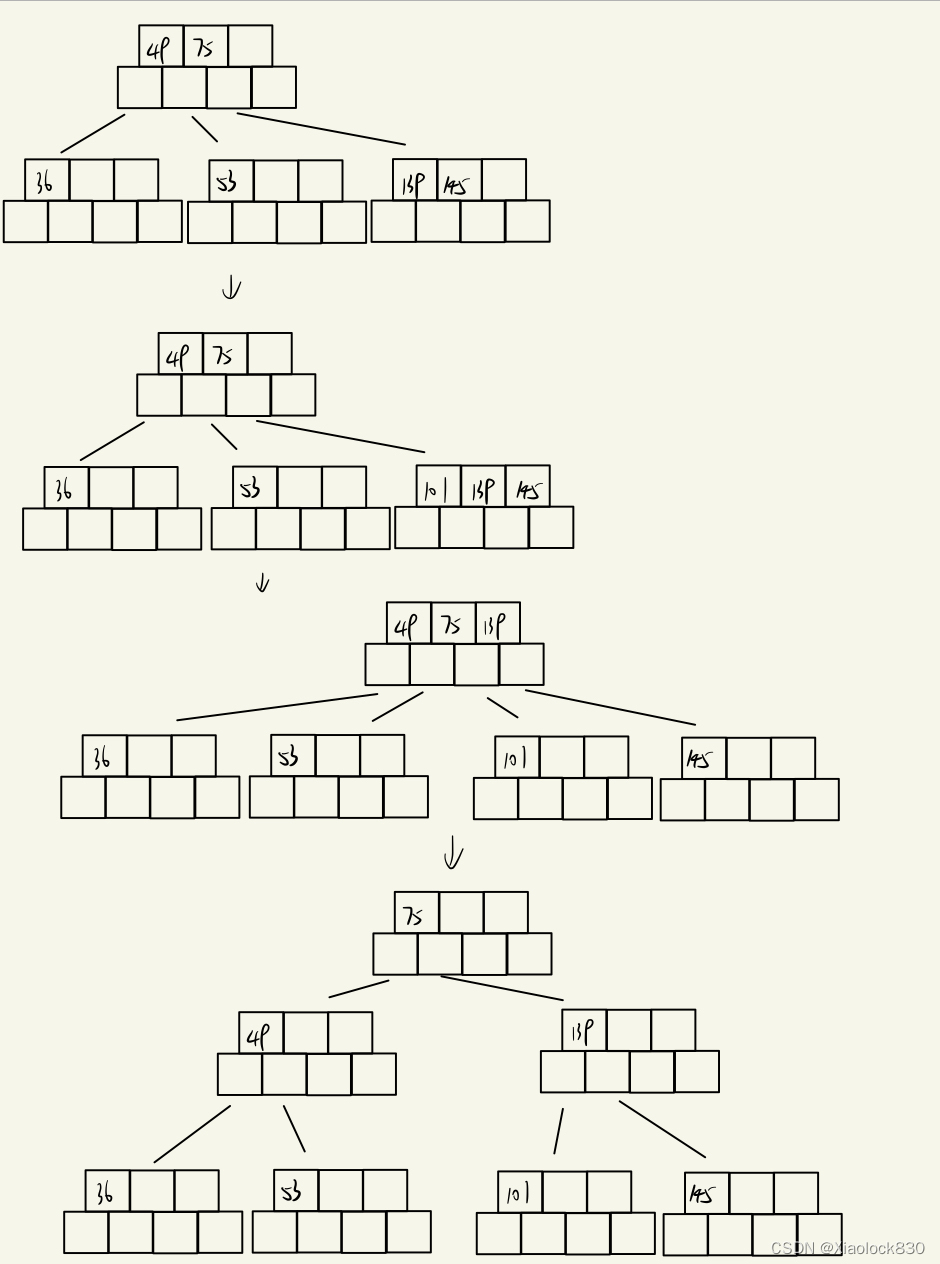
例如我们需要插入{53, 139, 75, 49, 145, 36, 101}

由于我们会涉及到数组下标越界的问题，因此我们在构建B-树时，一般会多构建一个关键字和孩子节点

首先是插入53，139，75
在插入时需要比较大小，让小的在前面，大的在后面，当我们插入到75时，发现数组满了，那么就需要分裂了
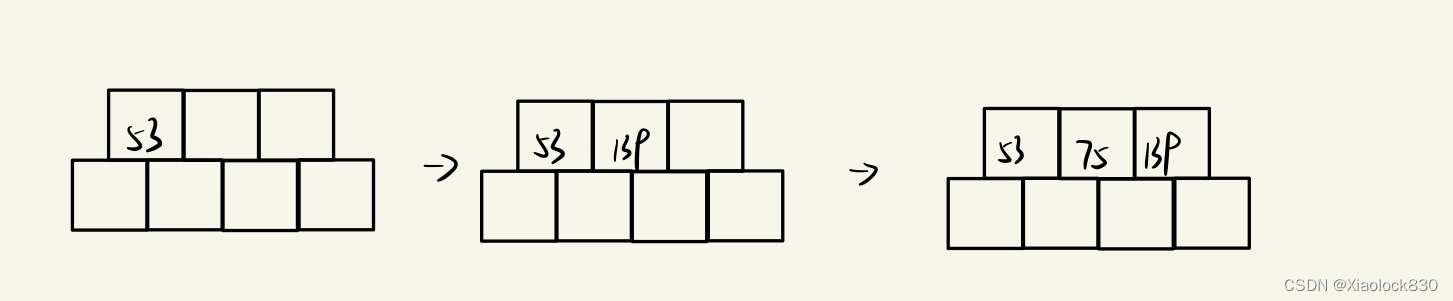
在这里插入图片描述
按照上面的原则——将其右半边的数据拷贝到新的孩子节点里，把最中间的一个数据拷贝到父亲节点，由于这个节点是根节点，所以我们不仅要创建一个新的节点，放右侧的数据139，并且还要再创建一个新的根节点，放中间的数据75
在这里插入图片描述
然后继续按照上面的原则插入49和145
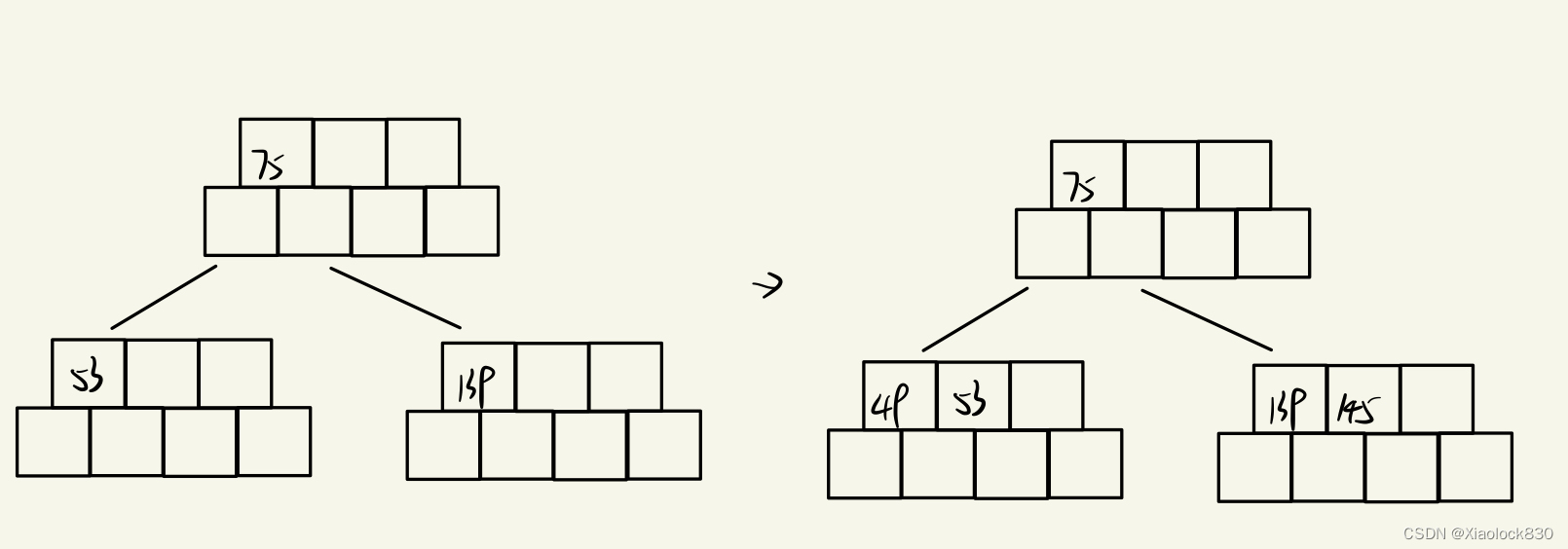
在这里插入图片描述
然后插入36，这时又有一个节点满了，因此需要创建一个节点，将右侧的数据53移动到新的节点，然后将中间的值49移动到其父亲节点处，需要满足从小到大的原则
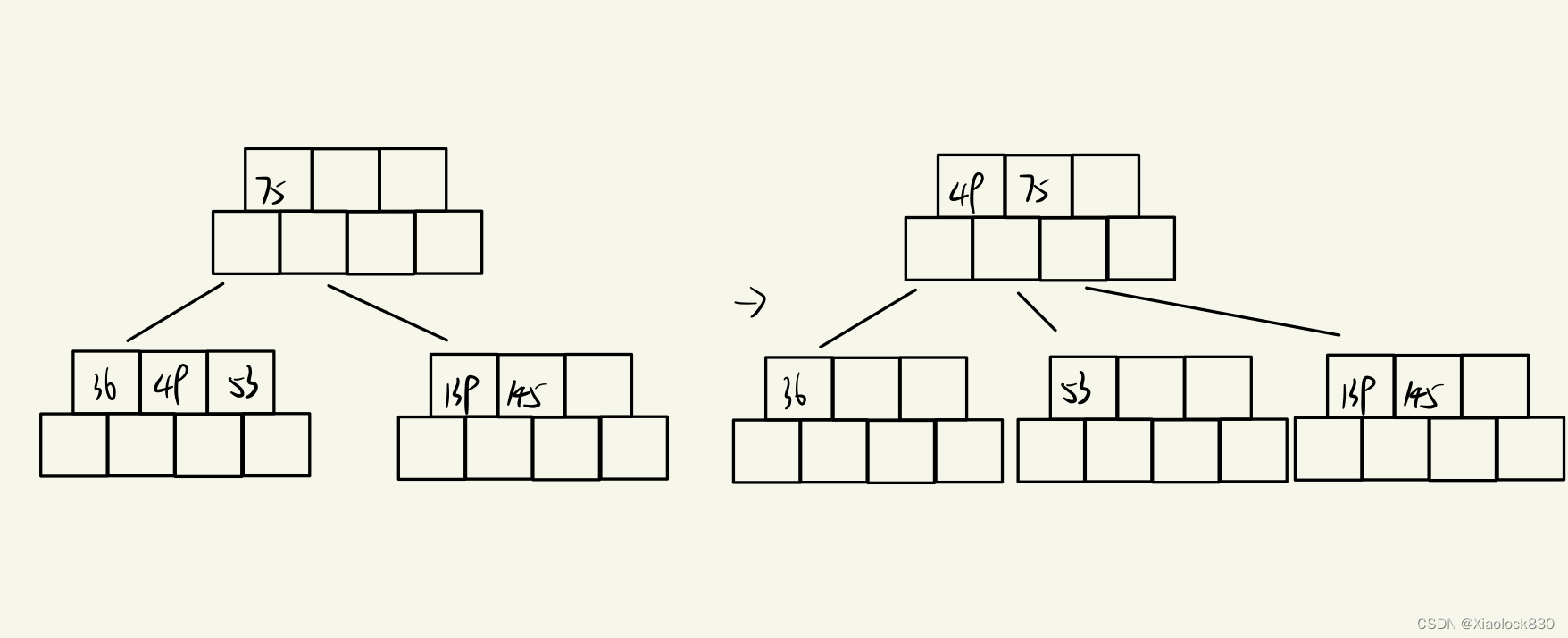
在这里插入图片描述
当我们插入101时，依旧需要分裂节点，将中间的值139移动到根节点时，根节点也满了，因此需要再次分裂，创建一个节点放右侧的值139，再创建一个新的根放75
在这里插入图片描述

MyBTree

根据上述思想，我们可以自己写一个B-树，这里分步骤讲解代码，因此代码是零散的，最后会展示完整的代码

节点

节点中不仅要存储关键字数组，孩子指针数组，还要有父亲节点，以及数据的个数

static class BTRNode{
    public int[] keys;
    public BTRNode[] subs;
    public BTRNode parent;
    public int usedSize;

    public BTRNode(){
        //默认多给一个方便分裂
        this.keys = new int[M];
        this.subs = new BTRNode[M + 1];
    }
}

参数

将M设置为3，也就是三叉树，我们上面在创建关键字和孩子数组时，由于需要数据的移动，所以默认多给一个元素的空间，这样可以方便我们移动

public static final int M = 3;

定义树的根节点

public BTRNode root;

插入方法

public boolean insert(int key){

先判断树中有没有数据，如果没有，那么就new一个节点，将数据插进入，把根设置成这个节点

//b树中没有数据
if(root == null){
    root = new BTRNode();
    root.keys[0] = key;
    root.usedSize++;
    return true;
}

如果树不为空，我们就需要找到合适的位置进行插入，这里写一个find方法，其参数是key

Pair<BTRNode,Integer> pair = find(key);

返回值是Pair，这个是我们自定义的一个对象，其中的Integer如果是-1，代表没有找到这个对象，而其中的BTRNode则是插入的具体位置

Pair定义如下

public class Pair <K,V>{
    private K key;
    private V val;

    public Pair(K key, V val) {
        this.key = key;
        this.val = val;
    }

    public K getKey() {
        return key;
    }

    public void setKey(K key) {
        this.key = key;
    }

    public V getVal() {
        return val;
    }

    public void setVal(V val) {
        this.val = val;
    }
}

然后我们来看一下find方法的实现

find

定义cur，从根开始找，定义parent，其作用是当cur为空时可以返回cur的上一个位置，上一个位置就是需要插入的位置

我们的cur从根的关键字数组0下标开始找，如果cur的key值小于key，说明不在左侧的分支上，如果等于，说明这个节点已经存在了，那么就返回cur和i

而如果大于，说明右侧的分支都大于key的值，所以我们应该向下找cur的孩子指针数组中的对应值，直到cur为空了，说明树中确实没有这个值，那么返回parent和-1，我们就可以在parent这个节点处插入下标了

这么说比较抽象，我们可以用一个具体的例子来说明

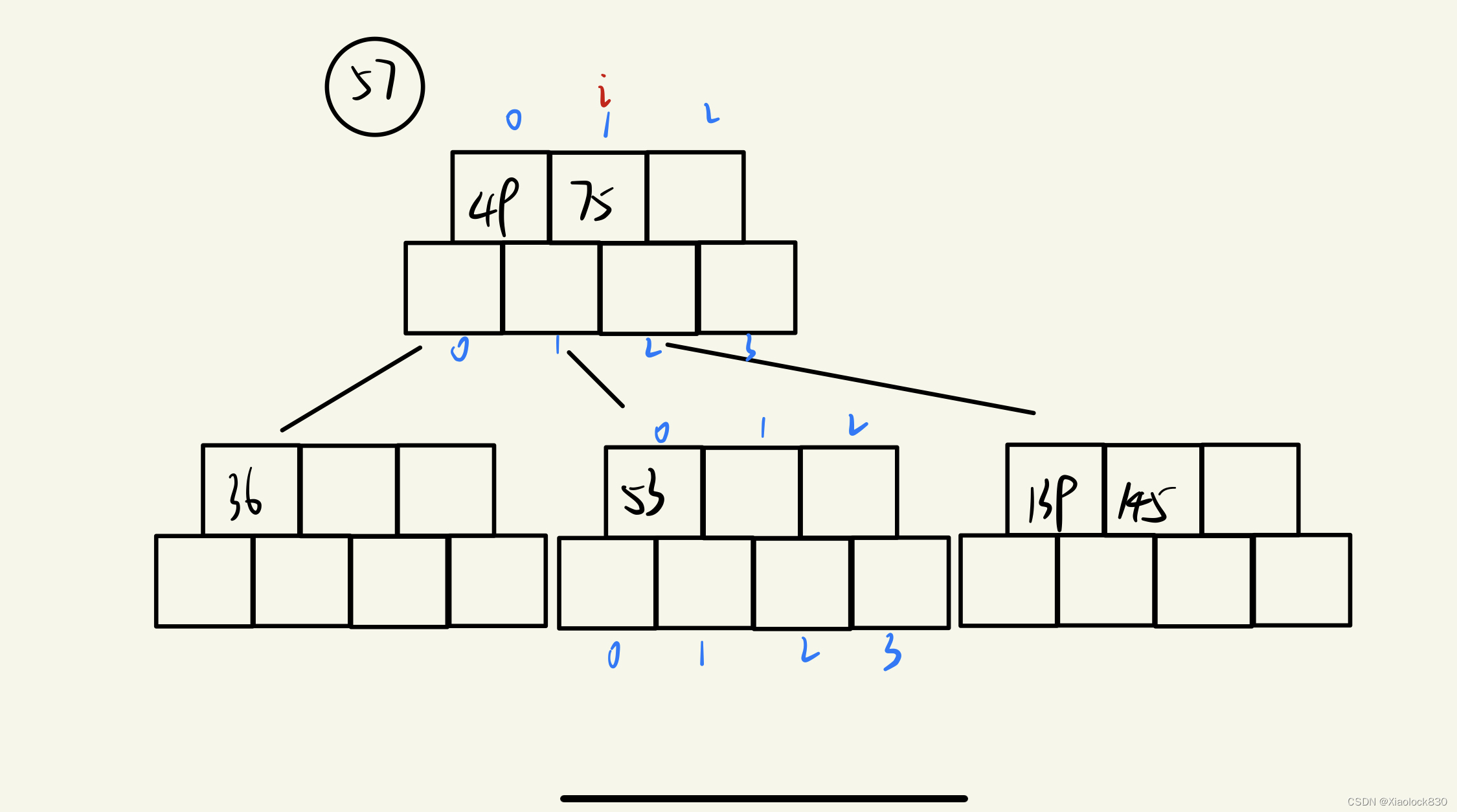
在这里插入图片描述
当我们要在上面这个树上插入57时，cur先是root，i从0开始遍历，可以发现当i == 1时，cur的keys[i]的值已经大于57了，而49和75之间的孩子分支对应的下标也正好是1，因此我们可以用cur = cur.subs[i]来进行迭代

而当cur遍历完53后，cur会变成cur.subs[1]，这时cur就变成空了，那么我们就返回parent，也就是53这个节点

详细代码如下：

public Pair<BTRNode,Integer> find(int key){
        BTRNode cur = root;
        BTRNode parent = null;
        while(cur != null){
            int i = 0;
            while(i < cur.usedSize){
                if(cur.keys[i] == key){
                    return new Pair<>(cur,i);
                } else if(cur.keys[i] < key){
                    i++;
                } else {
                    break;
                }
            }
            parent = cur;
            cur = cur.subs[i];
        }
        return new Pair<>(parent,-1);
    }

继续我们的插入过程
当返回的val不是-1，说明找到了这个值，那么直接返回false

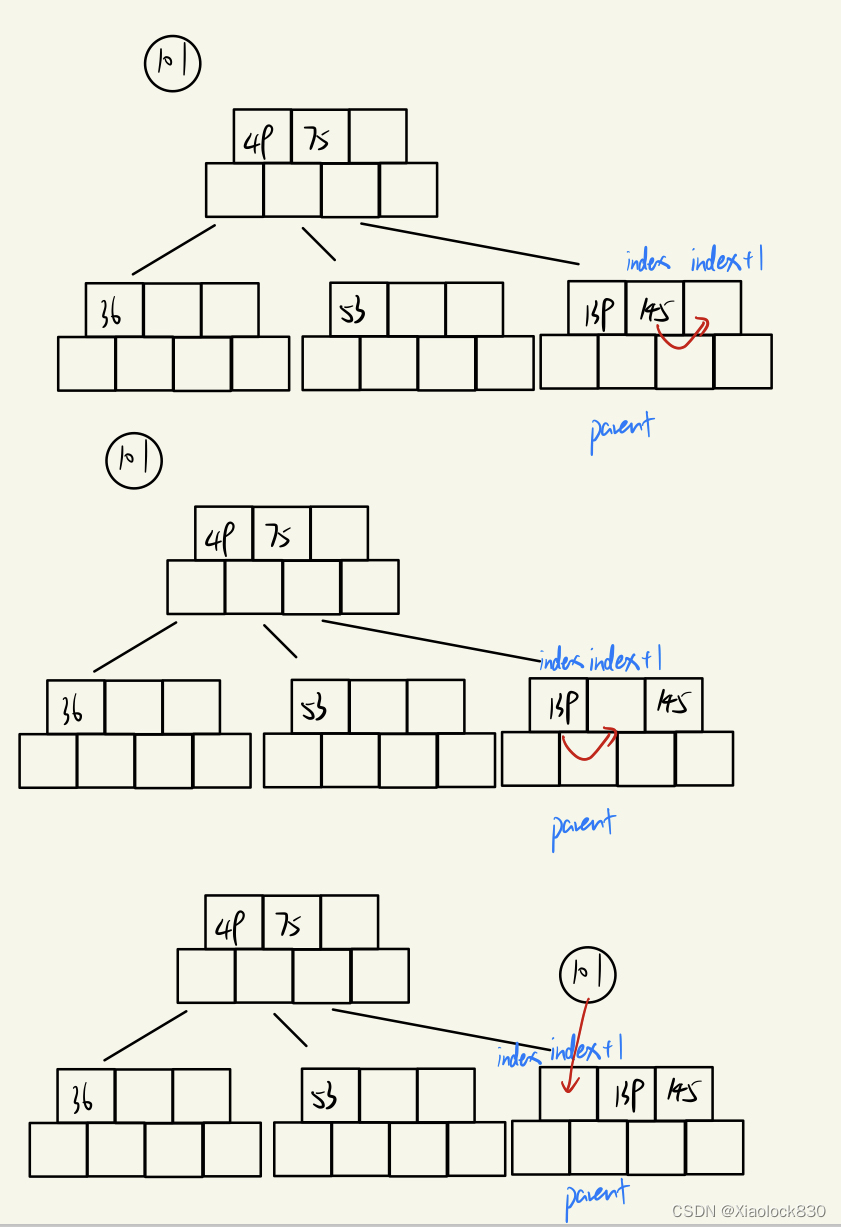
而如果不是-1，那么我们先拿到parent对应的节点，然后从后往前遍历，如果parent.keys[index]的值大于key，那么就把这个值往后挪，直到不大于，我们就让这个值变成key，然后让usedSize++

下面举一个详细的例子，大家可以对照这个图理解代码
在这里插入图片描述

//查看当前b树中是否有key
        if(pair.getVal() != -1){
            return false;
        }
        BTRNode parent = pair.getKey();
        int index = parent.usedSize - 1;
        for (; index >= 0 ; index--) {
            if(parent.keys[index] >= key){
                parent.keys[index + 1] = parent.keys[index];
            } else {
                break;
            }
        }
        parent.keys[index + 1] = key;
        parent.usedSize++;

接下来，我们就要看这个节点的值满没满，如果满了，就需要分裂节点，如果没满，就可以直接返回true了

if(parent.usedSize < M){
	//没满
    return true;
} else {
    //满了，需要分裂
    split(parent);
    return true;
}

分裂节点

参数是传进来的节点，定义名字为cur

private void split(BTRNode cur) {

首先创建一个新的节点，定义cur的父亲节点parent，然后找到cur的最中间的关键字mid，让i从mid加一开始，j从0开始

让cur的i一直加到usedSize - 1，把这中间的所有值都拷贝到新节点的0到后面的位置，需要注意的是，不仅要拷贝关键字，并且还要拷贝孩子指针

并且，我们还要判断cur的这些孩子节点是否为空，如果不是空，我们需要改变其父亲指针的指向，将其指向新的父亲：newNode

并且，由于subs数组比key数组多一个，我们在for循环结束后还需要再拷贝一次subs数组中的值

最后，把新节点的父节点设置为cur的父节点，然后将cur和newNode的有效数据个数都更改一下，这里cur的值还要再减1，这是因为一会我们还要把最中间的值放到父亲节点

BTRNode newNode = new BTRNode();
BTRNode parent = cur.parent;
int mid = cur.usedSize / 2;
int i = mid + 1;
int j = 0;

//将cur的右侧一半的数据拷贝到新节点
for ( ; i < cur.usedSize; i++){
    newNode.keys[j] = cur.keys[i];
    newNode.subs[j] = cur.subs[i];
    //将cur节点的孩子节点的父亲指针指向新的节点
    if(newNode.subs[j] != null){
        newNode.subs[j].parent = newNode;
    }
    j++;
}
newNode.subs[j] = cur.subs[i];
if(newNode.subs[j] != null){
    newNode.subs[j].parent = newNode;
}

//新节点的父亲指针指向cur的父亲
newNode.parent = parent;
//更新新节点和cur节点的有效数据个数
newNode.usedSize = j;
cur.usedSize = cur.usedSize - j - 1;

然后，如果我们的cur节点是根节点，那么先创建一个新的根节点，将其关键字数组的第一个元素赋值为cur的最中间的元素，然后将其孩子指针数组的第一个元素指向cur，让其第二个元素指向newNode，最后更改这两个节点的父亲指针为root即可返回

//当节点是根节点
if(cur == root){
    root = new BTRNode();
    root.keys[0] = cur.keys[mid];
    root.subs[0] = cur;
    root.subs[1] = newNode;
    root.usedSize = 1;
    cur.parent = root;
    newNode.parent = root;
    return;
}

如果我们的cur不是根节点，那么就需要将中间的值移动到cur的父亲节点，先定义endT为parent的最后一个关键字所在的位置，midVal为cur的最中间的关键字的值

通过从后往前遍历parent的关键字数组，找到合适的位置进行插入midVal，并且在移动时不仅要移动关键字，还要移动孩子指针，孩子指针比关键字要多1

然后把parent的usedSize++，如果这时parent的数据也满了，那么就需要继续分裂，我们直接递归即可

//移动父亲节点
int endT = parent.usedSize - 1;
int midVal = cur.keys[mid];
for (; endT >= 0; endT--){
    if(parent.keys[endT] >= midVal){
        parent.keys[endT + 1] = parent.keys[endT];
        parent.subs[endT + 2] = parent.subs[endT + 1];
    } else {
        break;
    }
}
parent.keys[endT + 1] = midVal;
parent.subs[endT + 2] = newNode;
parent.usedSize++;
if (parent.usedSize >= M){
    split(parent);
}

测试

大家可以用下面这个代码测试一下写的对不对，如果最终的结果是有序的，那么代码就是正确的

public static void main(String[] args) {
    MyBTree myBTree = new MyBTree();
    int[] arr = {53, 139, 75, 49, 145, 36, 101};
    for (int i = 0; i < arr.length; i++) {
        myBTree.insert(arr[i]);
    }
    myBTree.inorder(myBTree.root);
}

private void inorder(BTRNode root){
    if(root == null)
        return;
    for(int i = 0; i < root.usedSize; ++i){
        inorder(root.subs[i]);
        System.out.println(root.keys[i]);
    }
    inorder(root.subs[root.usedSize]);
}

完整代码

public class MyBTree {
    public static final int M = 3;

    static class BTRNode{
        public int[] keys;
        public BTRNode[] subs;
        public BTRNode parent;
        public int usedSize;

        public BTRNode(){
            //默认多给一个方便分裂
            this.keys = new int[M];
            this.subs = new BTRNode[M + 1];
        }
    }

    public BTRNode root;

    /**
     * 插入元素
     * @param key
     */
    public boolean insert(int key){
        //b树中没有数据
        if(root == null){
            root = new BTRNode();
            root.keys[0] = key;
            root.usedSize++;
            return true;
        }

        Pair<BTRNode,Integer> pair = find(key);
        //查看当前b树中是否有key
        if(pair.getVal() != -1){
            return false;
        }
        BTRNode parent = pair.getKey();
        int index = parent.usedSize - 1;
        for (; index >= 0 ; index--) {
            if(parent.keys[index] >= key){
                parent.keys[index + 1] = parent.keys[index];
            } else {
                break;
            }
        }
        parent.keys[index + 1] = key;
        parent.usedSize++;

        if(parent.usedSize < M){
            //没满
            return true;
        } else {
            //满了，需要分裂
            split(parent);
            return true;
        }
    }

    /**
     * 分裂
     * @param cur
     */
    private void split(BTRNode cur) {
        BTRNode newNode = new BTRNode();
        BTRNode parent = cur.parent;
        int mid = cur.usedSize / 2;
        int i = mid + 1;
        int j = 0;

        //将cur的右侧一半的数据拷贝到新节点
        for ( ; i < cur.usedSize; i++){
            newNode.keys[j] = cur.keys[i];
            newNode.subs[j] = cur.subs[i];
            //将cur节点的孩子节点的父亲指针指向新的节点
            if(newNode.subs[j] != null){
                newNode.subs[j].parent = newNode;
            }
            j++;
        }
        newNode.subs[j] = cur.subs[i];
        if(newNode.subs[j] != null){
            newNode.subs[j].parent = newNode;
        }

        //新节点的父亲指针指向cur的父亲
        newNode.parent = parent;
        //更新新节点和cur节点的有效数据个数
        newNode.usedSize = j;
        cur.usedSize = cur.usedSize - j - 1;

        //当节点是根节点
        if(cur == root){
            root = new BTRNode();
            root.keys[0] = cur.keys[mid];
            root.subs[0] = cur;
            root.subs[1] = newNode;
            root.usedSize = 1;
            cur.parent = root;
            newNode.parent = root;
            return;
        }

        //移动父亲节点
        int endT = parent.usedSize - 1;
        int midVal = cur.keys[mid];
        for (; endT >= 0; endT--){
            if(parent.keys[endT] >= midVal){
                parent.keys[endT + 1] = parent.keys[endT];
                parent.subs[endT + 2] = parent.subs[endT + 1];
            } else {
                break;
            }
        }
        parent.keys[endT + 1] = midVal;
        parent.subs[endT + 2] = newNode;
        parent.usedSize++;
        if (parent.usedSize >= M){
            split(parent);
        }
    }

    public Pair<BTRNode,Integer> find(int key){
        BTRNode cur = root;
        BTRNode parent = null;
        while(cur != null){
            int i = 0;
            while(i < cur.usedSize){
                if(cur.keys[i] == key){
                    return new Pair<>(cur,i);
                } else if(cur.keys[i] < key){
                    i++;
                } else {
                    break;
                }
            }
            parent = cur;
            cur = cur.subs[i];
        }
        return new Pair<>(parent,-1);
    }

    public static void main(String[] args) {
        MyBTree myBTree = new MyBTree();
        int[] arr = {53, 139, 75, 49, 145, 36, 101};
        for (int i = 0; i < arr.length; i++) {
            myBTree.insert(arr[i]);
        }
        myBTree.inorder(myBTree.root);
    }

    private void inorder(BTRNode root){
        if(root == null)
            return;
        for(int i = 0; i < root.usedSize; ++i){
            inorder(root.subs[i]);
            System.out.println(root.keys[i]);
        }
        inorder(root.subs[root.usedSize]);
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/103107.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【算法】单词接龙,合并区间, 二叉搜索树的最近公共祖先,旋转排序数组中的最小值看看有你会的吗？

【算法】单词接龙,合并区间, 二叉搜索树的最近公共祖先,旋转排序数组中的最小值看看有你会的吗？

算法学习有些时候是枯燥的&#xff0c;每天学习一点点 算法题目一. 单词接龙 II 题目描述java 解答参考二. 合并区间 题目描述java 解答参考三. 二叉搜索树的最近公共祖先 题目要求java实现方案四 寻找旋转排序数组中的最小值一. 单词接龙 II 题目描述 按字典 wordList 完成从…
阅读更多...
Azure RTOS 嵌入式无线网络框架简化物联网应用开发

Azure RTOS 嵌入式无线网络框架简化物联网应用开发

一、Azure RTOS概述 Azure RTOS 是一个实时操作系统 (RTOS)&#xff0c;适用于由微控制器 (MCU) 提供支持的物联网 (IoT) 和边缘设备&#xff0c; Azure RTOS 旨在支持高度受限设备&#xff08;电池供电&#xff0c;并且闪存容量不到 64 KB&#xff09;。简而言之&#xff0c;…
阅读更多...
某HR分享：2n和n+3的基数不一样，n+3比2n拿得多！仲裁期间不能入职新公司，千万别轻易仲裁，得不偿失！...

某HR分享：2n和n+3的基数不一样，n+3比2n拿得多！仲裁期间不能入职新公司，千万别轻易仲裁，得不偿失！...

被裁员时&#xff0c;要2n还是要n3&#xff1f;是否选择仲裁&#xff1f;一位hr说&#xff0c;跟走过仲裁的同学和律师朋友打听了下&#xff0c;原来2n和n3完全不一样。n3的n取的是“非私营单位从业人员平均工资”的三倍&#xff0c;杭州市是3.2万。2n的n取的是“全社会就业人员…
阅读更多...
Android设计模式详解之单例模式

Android设计模式详解之单例模式

前言 定义&#xff1a;确保某一个类只有一个实例&#xff0c;而且自行实例化并向整个系统提供这个实例。 使用场景&#xff1a;确保某个类有且仅有一个对象的场景&#xff0c;避免产生多个对象消耗过多的资源。比如要访问IO和数据库资源&#xff0c;应该考虑使用单例模式。 …
阅读更多...
JAVA开发（数据库表设计）

JAVA开发（数据库表设计）

对于大型系统数据库设计&#xff0c;需要进行一定的规划和规范&#xff0c;才能方便系统扩展和维护。一般系统的数据库设计要求&#xff0c;有数据库表系统规划&#xff0c;数据库表系统命名规范和设计规范。 一、数据库表系统规划 1、按系统规划或者按微服务规划 2、按业务…
阅读更多...
Matlab论文插图绘制模板第71期—三维饼图(Pie3)

Matlab论文插图绘制模板第71期—三维饼图(Pie3)

在之前的文章中&#xff0c;分享了Matlab饼图的绘制模板&#xff1a; 进一步&#xff0c;再来分享一下三维饼图的绘制模板。 先来看一下成品效果&#xff1a; 特别提示&#xff1a;Matlab论文插图绘制模板系列&#xff0c;旨在降低大家使用Matlab进行科研绘图的门槛&#xff0…
阅读更多...
最大子段和（动态规划详细解析）

最大子段和（动态规划详细解析）

最大子段和 题目描述 给出一个长度为 nnn 的序列 aaa&#xff0c;选出其中连续且非空的一段使得这段和最大。 输入格式 第一行是一个整数&#xff0c;表示序列的长度 nnn。 第二行有 nnn 个整数&#xff0c;第 iii 个整数表示序列的第 iii 个数字 aia_iai​。 输出格式 …
阅读更多...
读取excel文件read_excel()--Pandas

读取excel文件read_excel()--Pandas

1. 函数功能 读取excel文件&#xff0c;支持读取xls,xlsx,xlsm等类型的EXCEL文件。能够读取一个sheet表或多个sheet表 2. 函数语法 pandas.read_excel(io, sheet_name0, *, header0, namesNone, index_colNone, usecolsNone, squeezeNone, dtypeNone, engineNone, converte…
阅读更多...
MCMC算法

MCMC算法

一. MCMC算法定义 MCMC是Markov chain Monte Carlo的缩写&#xff0c;即马尔可夫链蒙特卡罗方法。MCMC是一组利用马尔可夫链从随机分布中取样的算法。生成的马氏链即是对于目标分布的近似估计。常见算法&#xff1a; Metropolis-Hastings算法Gibbs取样算法Hamiltonian Monte C…
阅读更多...
单片机AT89C51数码管数字时钟和闹钟二

单片机AT89C51数码管数字时钟和闹钟二

详细代码讨论加我QQ&#xff1a;1271370903 一、课题的方案设计与论证 1.1摘要 近年来随着计算机在社会领域的渗透和大规模集成电路的发展&#xff0c;单片机的应用正在不断地走向深入&#xff0c;由于它具有功能强&#xff0c;体积小&#xff0c;功耗低&#xff0c;价格便宜…
阅读更多...
【我的渲染技术进阶之旅】你可能永远猜不到为什么Filament项目命名为TNT？

【我的渲染技术进阶之旅】你可能永远猜不到为什么Filament项目命名为TNT？

文章目录一、疑惑为啥叫TNT&#xff1f;二、寻找真相2.1 百度TNT关键字2.2 GitHub issue2.3 GitHub Discussion三、总结一、疑惑为啥叫TNT&#xff1f; 在我之前的博客【我的渲染技术进阶之旅】如何编译Filament的windows版本程序&#xff1f; 有介绍如何编译Windows版本的Fil…
阅读更多...
React 18：Ref（获取DOM对象）

React 18：Ref（获取DOM对象）

ref介绍 React中所有的操作默认都是在React元素上进行&#xff0c;然后再通过虚拟DOM应用到真实页面上的。这样做的好处我们不在赘述。 虽然如此&#xff0c;在React中依然为我们提供了可以直接访问原生DOM对象的方式。ref就是干这个事的。 ref是reference的简写&#xff0c…
阅读更多...
【排序】详细聊聊归并排序（含非递归）

【排序】详细聊聊归并排序（含非递归）

目录 归并排序的基本思想&#xff1a; 递归算法&#xff1a; 递归算法的思路分析&#xff1a; 开辟数组的函数&#xff1a; 递归的函数&#xff1a; 非递归算法&#xff1a; 非递归的思路分析&#xff1a; 边界问题&#xff1a; 时间复杂度和空间复杂度分析&#xff1a…
阅读更多...
重建农场2.0：实景三维数据中心一站式解决方案

重建农场2.0：实景三维数据中心一站式解决方案

面向实景三维中国建设&#xff0c;如何扩大产能&#xff0c;不断提升实景三维数据中心的重建算力水平&#xff1f;如何满足快速迭代的需求&#xff0c;不断提升数据中心的应变能力&#xff1f;如何做到“一机多能”&#xff0c;不断外延数据中心的硬件价值&#xff1f;在前不久…
阅读更多...
jquery获取父/子iframe页面的URL

jquery获取父/子iframe页面的URL

最近因为要演示，做个临时ifame框架页面，因此子页面要根据父页面url来指定跳转。下面为ifame页面： 1、获取子页面url： var currentpath = window.location.pathname; console.log(currentpath); 输出为：/JG/TJ_JILU.aspx 2、获取父页面url： let currentTopHref = wind…
阅读更多...
IDEA 注释模版

IDEA 注释模版

类的主注释 /*** description TODO* author Gaoxueyong* date ${DATE} ${TIME}* version 1.0*/方法的注释 1、创建自己的分组 选择右侧Template Group并输入名称 2、创建自己的模版 选择自己创建的分组然后选择Live Template 然后在Template text框内写入 *** $description…
阅读更多...
脑图谱的一致性问题

脑图谱的一致性问题

脑图谱的意义及一致性问题 我们如何定义大脑的解剖结构&#xff0c;并将这些结构与大脑的功能联系起来&#xff0c;可以限制或增强我们对行为和神经系统疾病的理解大量可用的脑图谱给研究健康群体和患病人群的可重复性和描述大脑不同区域参与各种疾病的荟萃分析带来了问题——…
阅读更多...
全力推进企业数智赋能发展主线，低代码任重道远

全力推进企业数智赋能发展主线，低代码任重道远

信息化进程 纵观近半个世纪以来我国信息化的发展&#xff0c;经历了20世纪80年代以个人计算机普及应用为特征的数字化阶段&#xff08;信息化1.0&#xff09;&#xff1b;20世纪90年代中期以互联网大规模商用为特征的网络化阶段&#xff08;信息化2.0&#xff09;&#xff1b;…
阅读更多...
毕业设计 基于java web的网上招标系统

毕业设计 基于java web的网上招标系统

文章目录前言一、项目设计1. 模块设计注册用户部分管理员部分2. 实现效果二、部分源码最后前言 今天学长向大家分享一个 毕业设计项目: 基于java web的网上招标系统 一、项目设计 1. 模块设计 注册用户部分 1&#xff1a;查看网站流程&#xff1a;查看与网站有关的流程信息…
阅读更多...
ZBC成功上线PancakeSwap的糖浆池，并有望在不久上线Binance

ZBC成功上线PancakeSwap的糖浆池，并有望在不久上线Binance

近期流支付协议Zebec Protocol正在成为加密行业备受瞩目的Web3生态&#xff0c;其在此前与Visa合作推出可以使用加密货币进行支付的借记卡Zebec Card后&#xff0c;得到了Visa创始团队成员在技术、市场发展前景上的高度认可。与此同时&#xff0c;Zebec Protcocol也与尼泊尔财政…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023