前言:
二叉树属于数据结构的一个重要组成部分,很多小白可能被其复杂的外表所吓退,但我要告诉你的是“世上无难事,只怕有心人”,我将认真的对待这篇博客,我相信只要大家敢于思考,肯定会有所收获的,当我们攀过一座山,回头看去,可能当初畏惧的大山也不过如此。
目录
前言:
一,树的基本知识
1树的概念
2,树相关概念
二,二叉树的基本知识
1,二叉树的概念
2,特殊的二叉树:
三,二叉树的思路及代码实现(边讲解边写代码)
1,二叉树实现方式思考
2,前提准备(头文件和二叉树基本结构)
3,如何创建二叉树
4,二叉树的前,中,后序遍历
5,层序遍历
6,二叉树的拓展——堆(堆排序,TOPk问题)
1,堆的概念
2,堆的代码实现思考
3,向下排序
4,向上排序
5,Topk问题
1,建堆
2,堆如何插入呢?
3,堆顶数据如何删除呢?
一,树的基本知识
1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i
<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
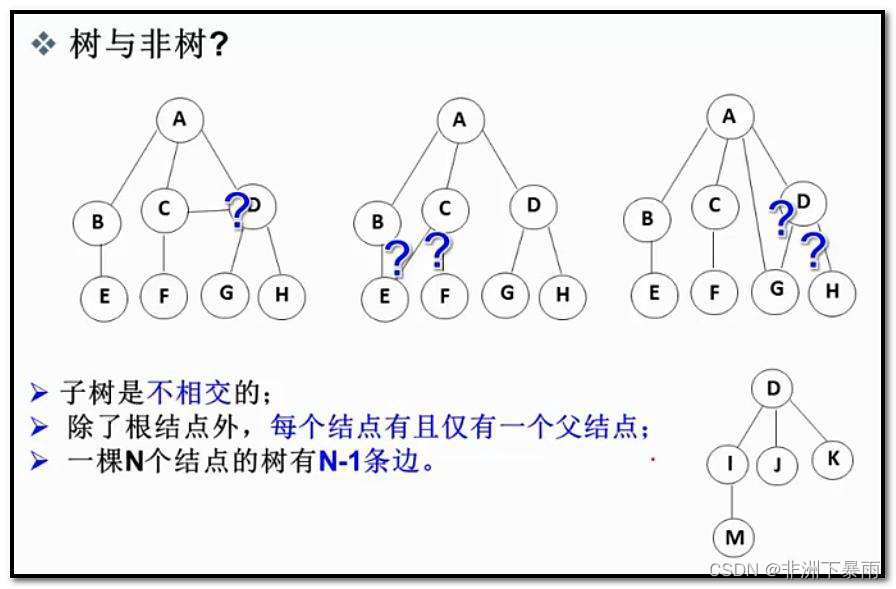
2,树相关概念

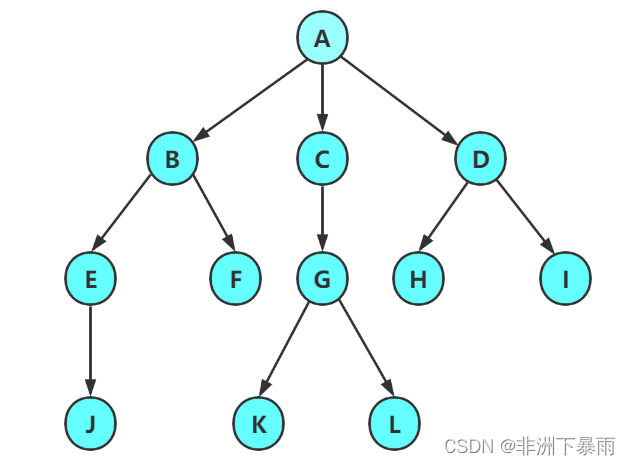
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
二,二叉树的基本知识
1,二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成

从上图可以看出:
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
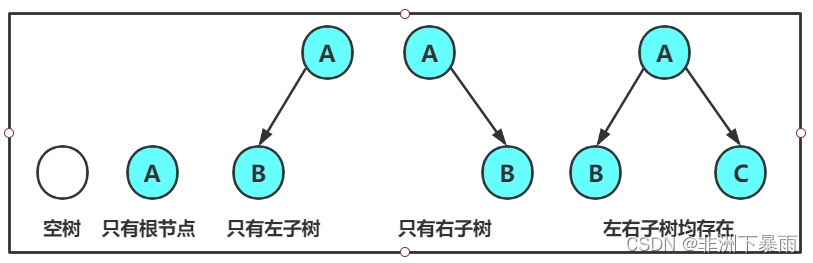
2,特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是
说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
三,二叉树的思路及代码实现(边讲解边写代码)
1,二叉树实现方式思考
想要用代码实现二叉树,我们首先要思考二叉树的结构特性,二叉树最多只有两个孩子,我们抓住这个关键特性,我们有两个实现方式:链表或者数组,我们只讲一种实现方式,链表实现二叉树,当然我讲完链表实现后,数组实现也不过是小菜一碟,现在正菜开始。
2,前提准备(头文件和二叉树基本结构)
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef char BTDataType;//BTDataType是char的别名,方便以后修改二叉树的数据类型
typedef struct BinaryTreeNode
{
BTDataType _data; //二叉树的存储数据
struct BinaryTreeNode* _left; //左孩子
struct BinaryTreeNode* _right; //右孩子
}BTNode;3,如何创建二叉树
要求:给你一串字符,要求你根据字符前序遍历创建二叉树
字符:"ABD##E#H##CF##G##"
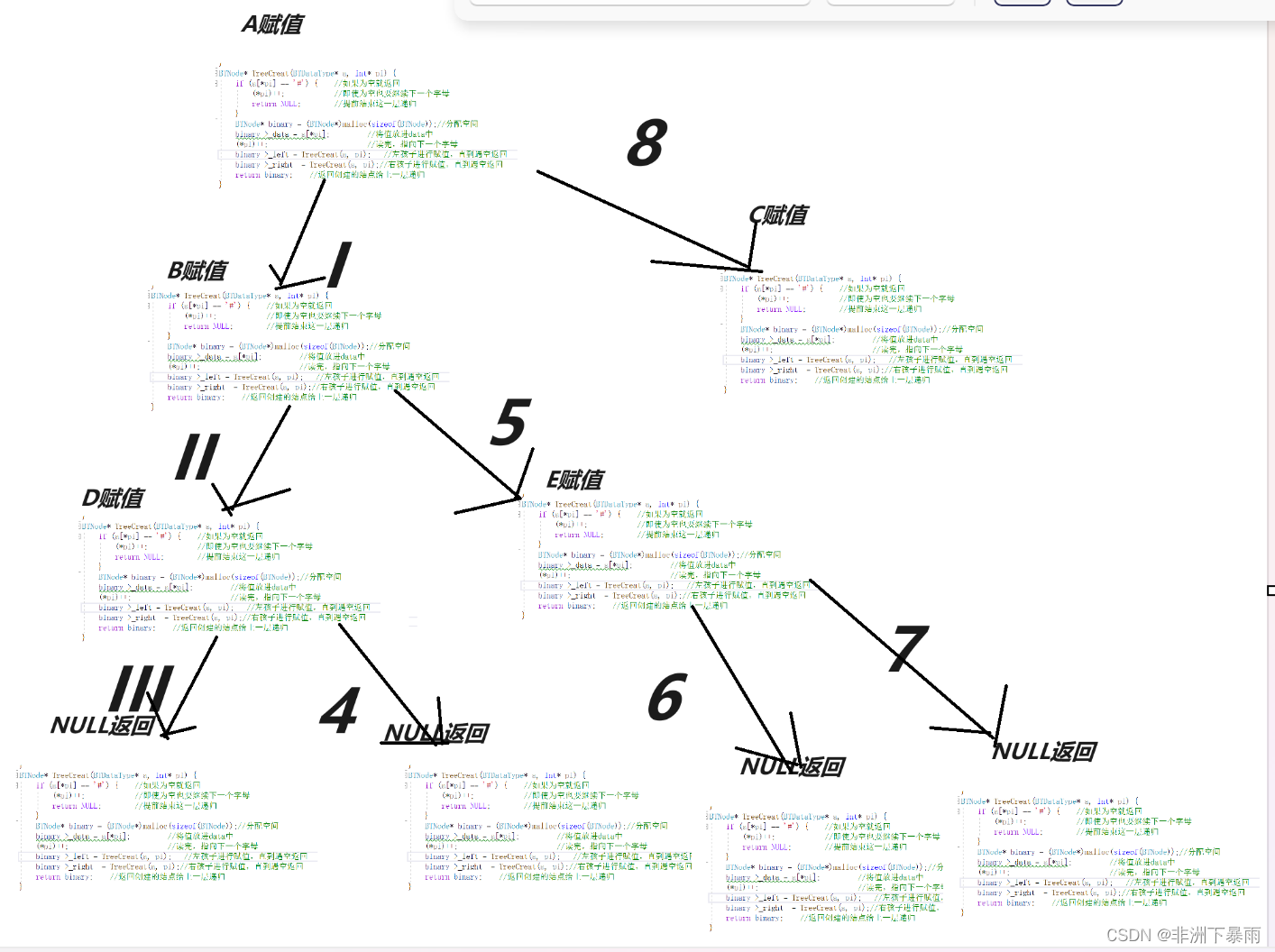
利用字符创建二叉树,一开始我们肯定是一头雾水,我们首先自己在纸上试试创建二叉树
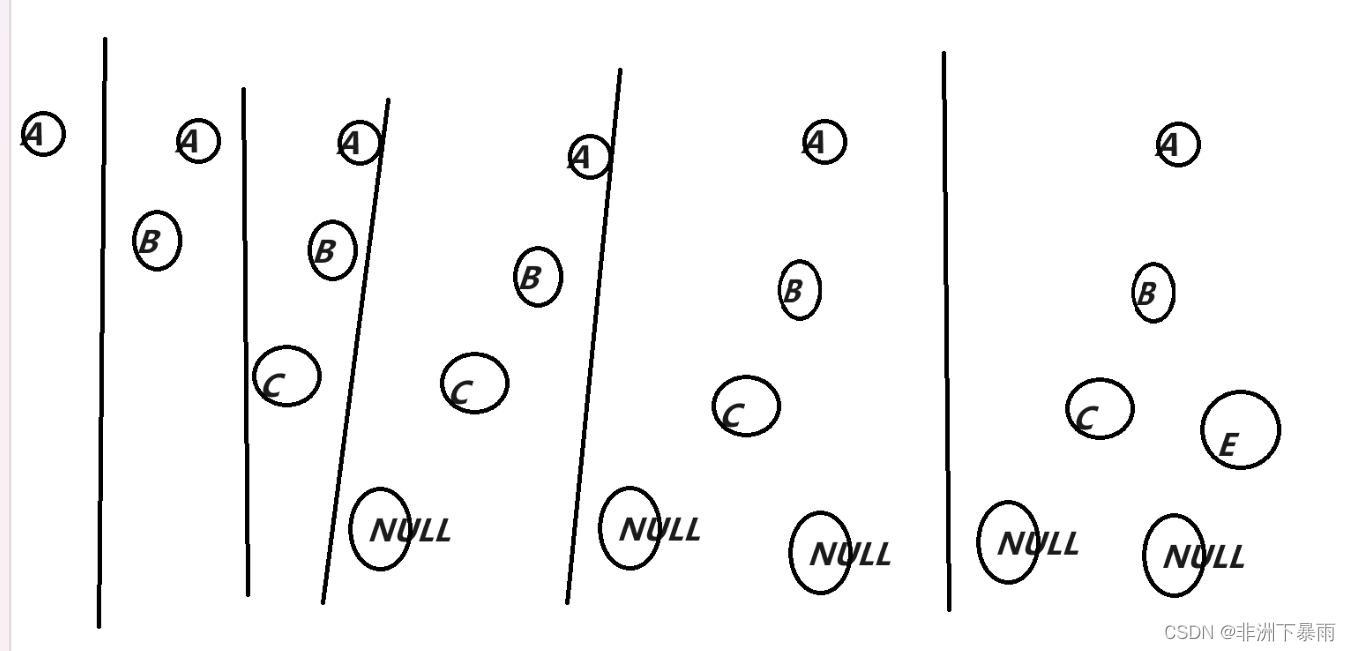
不知道大家有没有发现规律,因为是前序遍历,因此是对根A进行赋值,然后是左孩子B,像C如果左孩子是NULL,就返回上一个根C对右孩子进行赋值,右孩子如果非空,就继续对右孩子的左孩子进行赋值,遇到空就返回对右孩子的右孩子赋值,直到全为空就返回到B。
那么这个思路我们该怎么实现呢,不知道大家有没有发现这个可以拆分为一个个类似的子问题,那么结果就呼之欲出了-----递归。接下来跟上代码继续讲解一遍思路
BTNode* TreeCreat(BTDataType* a, int* pi) {
if (a[*pi] == '#') { //如果为空就返回
(*pi)++; //即使为空也要继续下一个字母
return NULL; //提前结束这一层递归
}
BTNode* binary = (BTNode*)malloc(sizeof(BTNode));//分配空间
binary->_data = a[*pi]; //将值放进data中
(*pi)++; //读完,指向下一个字母
binary->_left = TreeCreat(a, pi); //左孩子进行赋值,直到遇空返回
binary->_right = TreeCreat(a, pi);//右孩子进行赋值,直到遇空返回
return binary; //返回创建的结点给上一层递归
}
BTNode* BinaryTreeCreate(BTDataType* a,int n, int* pi) {
*pi = 0; //用这个来记录读取的数据到哪里了
return TreeCreat(a,pi); //开始递归读值
}
4,二叉树的前,中,后序遍历
二叉树前,中,后遍历呢?大家先想想前序创建二叉树,有没有发现遍历只要按照创建时的思路就行了,那么话不多说·直接上前序代码
void BinaryTreePrevOrder(BTNode* root) {
if (root == NULL) { //老规矩,遇空返回
printf("#");
return;
}
printf("%c", root->_data); //按照前序顺序先打印根
BinaryTreePrevOrder(root->_left); //开始进入左孩子,进入之后会打印左孩子,一直走到NULL
BinaryTreePrevOrder(root->_right);//开始进入右孩子,进入之后会打印左孩子,一直走到NULL
}中序代码
void BinaryTreeInOrder(BTNode* root) {
if (root == NULL) { //防止非法访问,直接判断是否为空
printf("#");
return;
}
BinaryTreeInOrder(root->_left); //进入递归,先直到最左的叶结点
printf("%c", root->_data); //开始打印
BinaryTreeInOrder(root->_right);//根和左孩子都遍历了开始进入右孩子并打印
}相信聪明的你可以独自写出后序遍历了吧!!!
5,层序遍历
前中后遍历还有迹可寻,那层序遍历应该怎么入手呢?层序遍历的如果光按照树的特性是不太好入手的,但是我们想一下,假设打印根节点,再打印它的两个孩子,再打印根节点孩子的所以孩子,这个中间是不是有一个顺序关系,你有没有想到队列呢,这样的话是不是可以依次拿到数据呢?在里面还有一个重要的关系,就是一个父亲结点会有两个孩子,也就意味着入队列的速度是远大于出队列的速度的,想完这些我们就可以写代码了。想看队列的源代码你们可以看我的往期文章。
void BinaryTreeLevelOrder(BTNode* root) {
Queue* q = (Queue*)malloc(sizeof(Queue));//创建队列
QueueInit(q); //初始化队列
QueuePush(q, root); //先将根入队列
while (q->_front != q->_rear ) { //这个时候队列头等于尾,意味着队列为空了
if (q->_front->_data != NULL) { //入队列第一个非空元素的两个孩子
QueuePush(q, q->_front->_data->_left);
QueuePush(q, q->_front->_data->_right);
printf("%c", q->_front->_data->_data);//打印队列第一个元素的休息
}
else
printf("#"); //为空也要打印
QueuePop(q); //出掉原先的第一个元素,第二个元素顶上
}
}6,二叉树的拓展——堆(堆排序,TOPk问题)
1,堆的概念
堆就是一个完全二叉树
大堆就是父亲节点一定大于孩子节点
小堆就是父亲节点小于孩子节点
2,堆的代码实现思考
堆是二叉树,我们同样可以用链表和数组实现,我们这里为了突出堆的特性和作用,我们这里用数组实现,在实现前我们有两个规则会帮助我们进行排序,大家先记住下标规律,规则的条件是,根节点在数组中的位置为1,孩子节点是按顺序存储的,先左孩子,后右孩子
左孩子下标=父节点下标/2+1
右孩子下标=父节点下标/2+2、
父节点下标=(孩子节点下标-1)/2 //因为int是没有小数的,1/2=0.所以左右节点没必要区分
3,向下排序
首先声明,堆排序不是绝对有序,而是父节点相比孩子节点是有序的,但兄弟节点和同一层节点不一定有序。
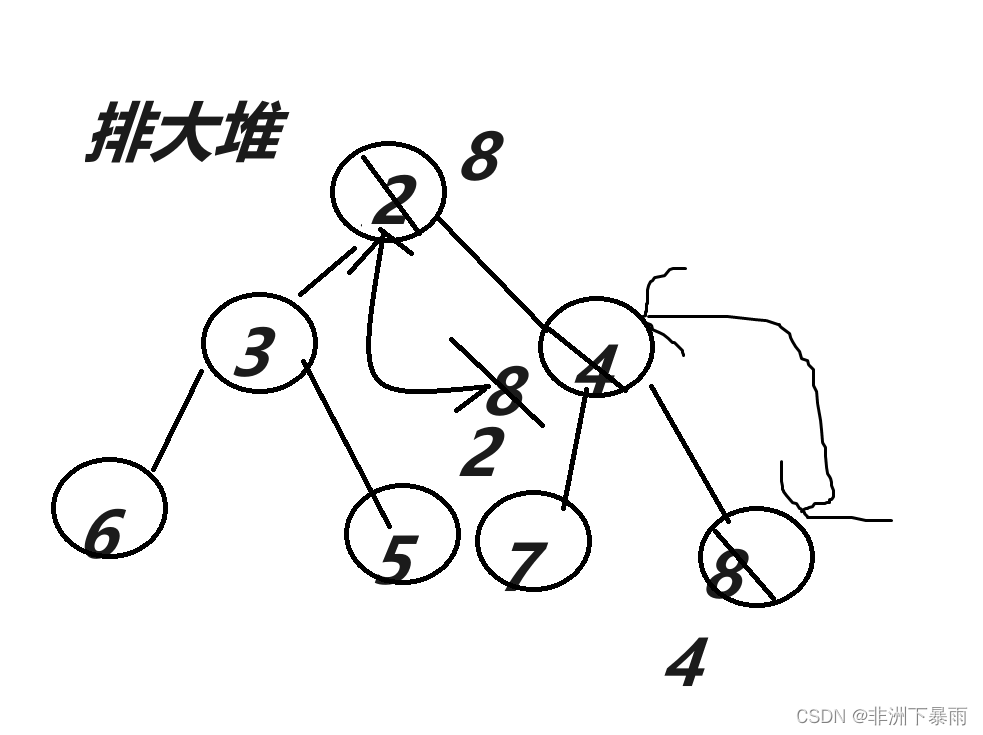
向下排序是如何排的呢?顾名思义,就是从根节点开始和孩子节点比较,如果大小不符合堆的特性,就交换位置,直到堆的叶结点,如果大小符号就直接结束,开始下一层排序,我们要利用父节点和孩子节点的位置才能进行比较和交换
接下来看一下小堆排序的图

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size; //堆的大小
int _capacity;//堆的总容量
}Heap;
void Adjustdown(HPDataType* a, int n,int capcity) {
int parent = n; //参数传来排序的位置下标
int child = parent * 2 + 1; //找到孩子节点下标
while (child < capcity) { //防止数组越界
if (child + 1 < capcity && a[parent] > a[child + 1] && a[child + 1] < a[child]) {
swap(a + parent, a + child + 1); //交换
parent = child + 1; //父子换为左孩子字节的下标,开始下一轮交换
}
else if (a[parent] > a[child]) {
swap(a + parent, a + child);
parent = child; //父子换为右孩子字节的下标,开始下一轮交换
}
else
break; //无需交换,直接结束
child = parent * 2 + 1; //更新孩子节点的位置下标
}
}4,向上排序
向上排序和向下排序相反,它是从子节点到父节点,到根节点就会强制终止,
void Adjustup(HPDataType* a, int n) {
int parent = (n - 1) / 2;//通过参数找到父节点
int child = n; //找到孩子节点
while (child > 0) {
if (a[child] < a[parent])
swap(a + child, a + parent);
else
break; //如果不需要交换就停止,前提是堆是有序的
child = parent; //将子节点换位父节点,向上排序
parent = (child - 1) / 2; //父节点继续向上
}
}现在你有没有想为什么写向上排序和向下排序,其实向上排序和向下排序就像插入排序和冒泡排序的作用,只不过是用于堆的排序,但想要将一个毫无规律的堆排序是需要很多个向上排序和向下排序的,我们可以利用循坏来进行重复的排序。
5,Topk问题
堆排序的一个很重要的作用就是Topk问题,简而言之就是排行榜,相比与冒泡的o(n^2),堆排序的时间复杂度是nlogn。
1,建堆
首先要求Topk,我们需要一个容量为k的堆,这样我们才能进行排序,因此我们首先来建堆,并且将堆进行排序
void HeapCreate(Heap* hp, HPDataType* a, int n) {
assert(hp); //防止非法访问导致程序崩溃
hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n); //开辟堆空间
assert(hp->_a); //判断是否开辟成功
for (int i = 0; i < n; i++)
hp->_a[i] = a[i]; //将数据全部输入堆,注意此时无序
hp->_capacity = n; //记录容量
hp->_size = n; //记录大小
for(int i=(n-2)/2;i>=0;i--) //找到第一个倒数的父亲节点,并且逐个向下排序直到根
Adjustdown(hp->_a ,i,n);
for (int i = 0; i < n; i++)
printf("%d ", hp->_a[i]); //打印方便观察
}2,堆如何插入呢?
从数组的角度来看,我们可以先不管大小关系,直接将新数据放到末尾再来考虑顺序问题,将数据放到末尾之后排序就简单了,我们直接用一个向上排序就可以是堆再次有序了
void HeapPush(Heap* hp, HPDataType x) {
if (hp->_capacity == hp->_size) { //检查堆的剩余空间
HPDataType* b;
b= (HPDataType*)realloc(hp->_a ,sizeof(HPDataType) * (hp->_capacity + 3)); //一次开辟三个内存
assert(b); //判断是否开辟成功
hp->_a = b; //将开辟好的堆放入原位置
hp->_capacity += 3; //调整堆的容量记录
}
hp->_a[hp->_size] = x; //放到数组末尾
Adjustup(hp->_a, hp->_size); //向上调整一次就有序了
hp->_size++;
}3,堆顶数据如何删除呢?
堆顶数据的删除看似是一个复杂的问题,我们要想清楚,如果直接把堆顶删除,然后之后的数据就依次往前推,但是会有一个问题,往前推一定是有序的吗?我们之前讲了,堆同层是不一定有序的,如果随意的往前覆盖,就会导致原先同层小的数据成为了父节点,此时会产生蝴蝶效应,我们无法判断有多少个无序了,因此我们要另辟蹊径,想一想如果我们把第一个时间和最后一个数据交换,然后把最后一个数据无视,那么是不是只要根节点的数据是无序的,那么此时我们只需要堆根进行一次向下排序不就有序了吗?
void HeapPop(Heap* hp) {
assert(hp); //防止非法访问
assert(hp->_a);
swap(hp->_a+0, hp->_a+hp->_size -1);//交换第一个和最后一个数据
Adjustdown(hp->_a, 0, hp->_size-1);//直接进行一次向下排序完成
hp->_size--;
}博客耗时颇多,希望大家点赞加收藏,可以评论区交流