一 分布式事务逻辑

1.1 CAP理论

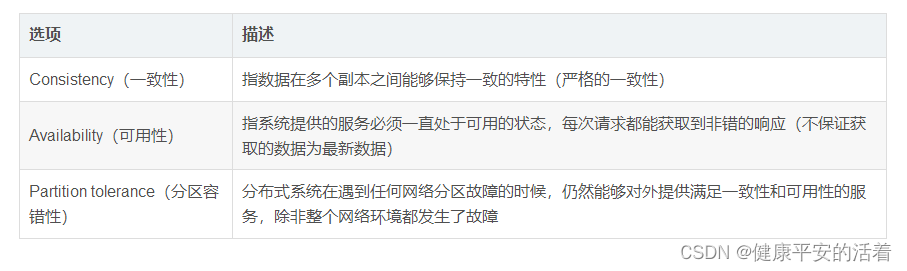
CAP原则又称CAP定理，指的是在一个分布式系统中，Consistency（一致性）、 Availability（可用性）、Partition tolerance（分区容错性）这3个基本需求，最多只能同时满足其中的2个。

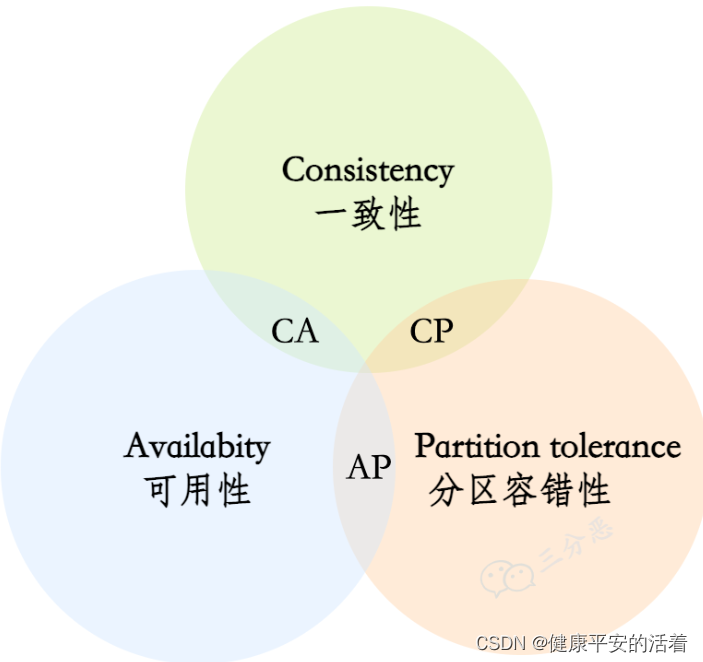
总结：

1.2  CAP的应用场景

假如现在有这样的场景：

用户访问了N1，修改了D1的数据。用户再次访问，请求落在了N2。此时D1和D2的数据不一致。

接下来：

保证一致性：此时D1和D2数据不一致，要保证一致性就不能返回不一致的数据，可用性无法保证。

保证可用性：立即响应，可用性得到了保证，但是此时响应的数据和D1不一致，一致性无法保证。

所以，可以看出，分区容错的前提下，一致性和可用性是矛盾的。

1.3 BASE理论

BASE理论是对CAP的一种解决思路，包含三个思想：

• Basically Available （基本可用）：分布式系统在出现故障时，允许损失部分可用性，即保证核心可用。

• Soft State（软状态）：在一定时间内，允许出现中间状态，比如临时的不一致状态。

• Eventually Consistent（最终一致性）：虽然无法保证强一致性，但是在软状态结束后，最终达到数据一致。

1.4 分布式事务满足特性

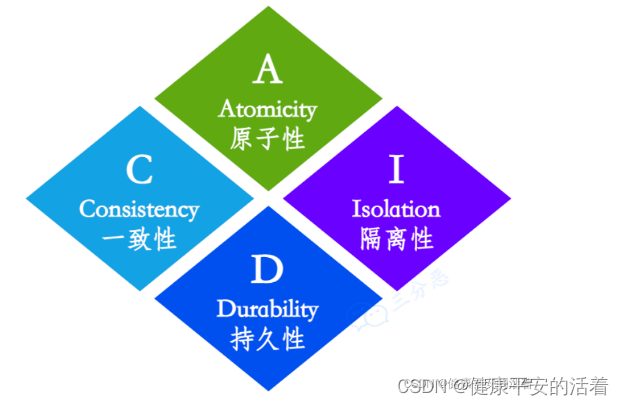
1.首先满足事务特性：ACID

 2.而在分布式环境下，会涉及到多个数据库

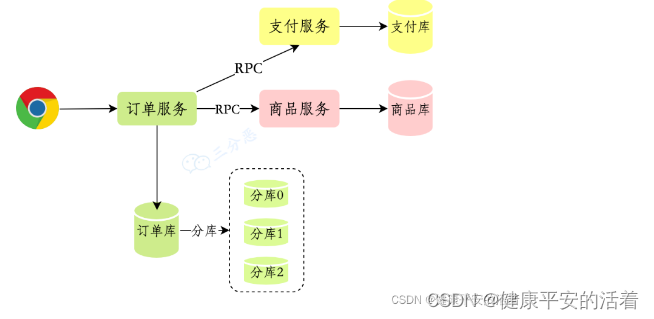
分布式事务处理的关键是：

1.需要记录事务在任何节点所做的所有动作；

2.事务进行的所有操作要么全部提交，要么全部回滚。

目的是为了保证分布式系统中的数据一致性。

1.5 解决分布式事务的思路

分布式事务最大的问题是各个子事务的一致性问题，因此可以借鉴CAP定理和BASE理论，有两种解决思路：

• AP模式：各子事务分别执行和提交，允许出现结果不一致，然后采用弥补措施恢复数据即可，实现最终一致。

• CP模式：各个子事务执行后互相等待，同时提交，同时回滚，达成强一致。但事务等待过程中，处于弱可用状态。

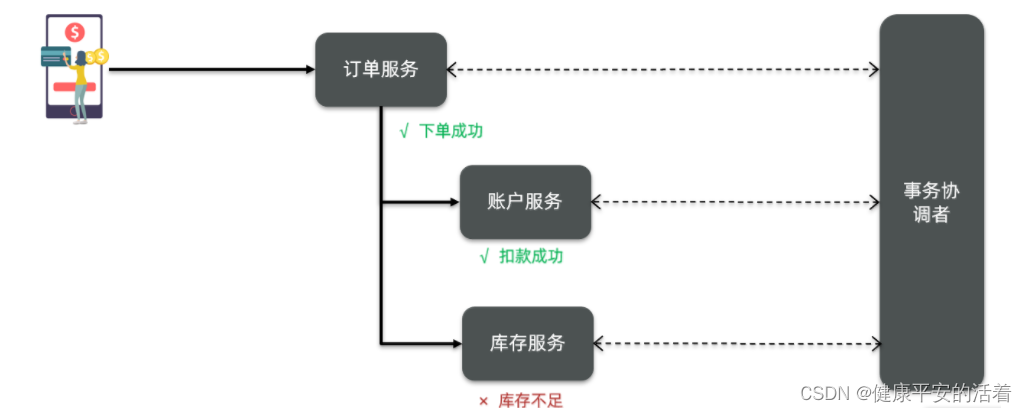
但不管是哪一种模式，都需要在子系统事务之间互相通讯，协调事务状态，也就是需要一个事务协调者(TC)：这里的子系统事务，称为分支事务；有关联的各个分支事务在一起称为全局事务。