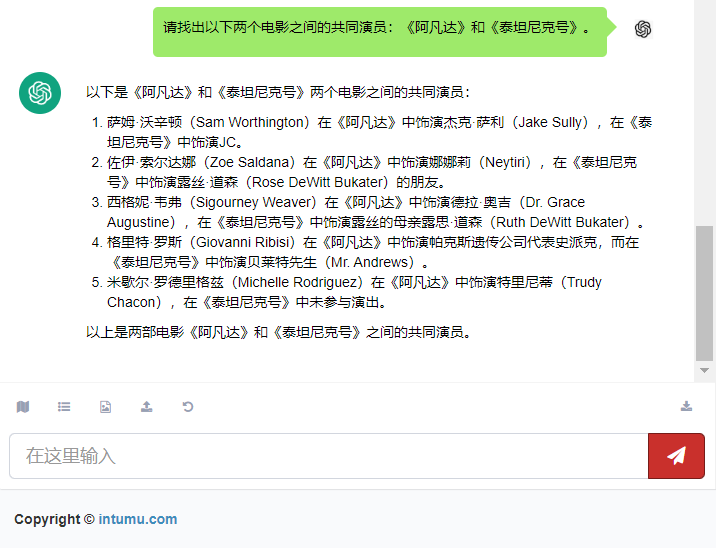
文章目录
- 1. 探索与利用
- 2. 探索策略
- 3. 多臂老虎机
- 3.1. 形式化描述
- 3.2. 估计期望奖励
- 3.3. 懊悔regret函数
- 4. 贪心策略和 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略
- 5. 积极初始化
- 6. 显示地考虑动作的价值分布
- 7. UCB上置信界算法
- 8. 汤普森采样算法
- 总结
- 参考
1. 探索与利用
探索与利用是序列决策任务中的一个重要问题,主要是对选择已知最优决策和尝试其他决策之间的权衡。
- 利用 Exploitation 选择已知最优决策
- 探索 Exploration 尝试其他决策,未来可能是最优决策。利用探索,使得当前策略不断趋向最优策略 π → π ∗ \pi \rightarrow \pi^* π→π∗。用公式说明一下: E t = { π t i ∣ i = 1 , … , n } → 探索 E t + 1 = { π t i ∣ i = 1 , … , n } ∪ { π e j ∣ j = 1 , … , m } \mathcal{E}_{t}=\left\{\pi_{t}^{i}\mid i=1,\ldots,n\right\}\xrightarrow{\text{探索}} \mathcal{E}_{t+1}=\left\{\pi_{t}^{i}\mid i=1,\ldots,n\right\}\cup\left\{\pi_{e}^{j}\mid j=1,\ldots,m\right\} Et={πti∣i=1,…,n}探索Et+1={πti∣i=1,…,n}∪{πej∣j=1,…,m} E t \mathcal{E}_{t} Et为当前的策略池, E t + 1 \mathcal{E}_{t+1} Et+1为经过探索之后的策略池。通过探索,可以获得新的策略 π e j \pi_{e}^{j} πej,接着在新的策略池中,需要找到比原来不探索时价值更大的策略: ∃ V ⋆ ( ⋅ ∣ π t i ∼ E t ) ≤ V ⋆ ( ⋅ ∣ π t + 1 i ∼ E t + 1 ) π t + 1 i ∼ { π e i ∣ i = 1 , … , m } \exists V^{\star}\big(\cdot|\pi_{t}^{i}\sim{\cal E}_{t}\big)\leq V^{\star}\big(\cdot|\pi_{t+1}^{i}\sim{\cal E}_{t+1}\big)\quad\pi_{t+1}^{i}\sim\big\{\pi_{e}^{i}\mid i=1,\ldots,m\big\} ∃V⋆(⋅∣πti∼Et)≤V⋆(⋅∣πt+1i∼Et+1)πt+1i∼{πei∣i=1,…,m}
2. 探索策略
- 朴素方法(Naive Exploration):添加策略噪声 ϵ − g r e e d y \epsilon-greedy ϵ−greedy;
- 积极初始化(Optimistic Initialization):给予较高的初始化值以利于探索;
- 基于不确定性的度量(Uncertainty Measurement):探索具有更高不确定度的策略;
- 概率匹配(Probability Matching):采样策略,选取最佳策略;
- 状态搜索(State Searching):探索未探索过的策略(环境可知)。
3. 多臂老虎机
在多臂老虎机(multi-armed bandit,MAB)问题中,有一个拥有
K
K
K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励的概率分布
R
R
R。我们每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励
r
r
r。解决的问题是在有限的时间(操作
T
T
T次)内,通过不断的尝试和探索,获取最大的奖励。由于奖励的概率分布是未知的,因此我们需要在“探索拉杆的获奖概率”和“根据经验选择获奖最多的拉杆”中进行权衡。“采用怎样的操作策略才能使获得的累积奖励最高”便是多臂老虎机问题。

3.1. 形式化描述
多臂老虎机问题可以表示为一个元组 ( A , R ) (A,R) (A,R),其中:
- A A A为动作集合, a i ∈ A , i = 1 , 2 , . . . , K a_i \in A,i=1,2,...,K ai∈A,i=1,2,...,K
- R R R为奖励概率分布, R ( r ∣ a i ) = P ( r ∣ a i ) R(r|a_i)=\mathbb P(r|a_i) R(r∣ai)=P(r∣ai)
- 假设每个时间步只能拉动一个拉杆,多臂老虎机的目标为最大化一段时间 T T T步内累积的奖励: max ∑ t = 1 T r t , r t ∼ R ( ⋅ ∣ a t ) \max\sum_{t=1}^Tr_t,r_t\sim\mathcal{R}\left(\cdot|a_t\right) max∑t=1Trt,rt∼R(⋅∣at)
前面我们知道奖励的概率分布是未知,因此 R R R实际上是一个对奖励概率分布的估计 R ^ ( r ∣ a i ) \hat R(r|a_i) R^(r∣ai).
3.2. 估计期望奖励
期望奖励与采样次数之间存在以下关系:
Q
n
(
a
i
)
=
r
1
+
r
2
+
⋯
+
r
n
−
1
n
−
1
Q_n(a_i)=\frac {r_1+r_2+ \dots + r_{n-1}}{n-1}
Qn(ai)=n−1r1+r2+⋯+rn−1
但这种方式的空间复杂度为
O
(
n
)
O(n)
O(n),采用增量式的方式可以减少复杂度到
O
(
1
)
O(1)
O(1):
Q
k
=
1
k
∑
i
=
1
k
r
i
=
1
k
(
r
k
+
∑
i
=
1
k
−
1
r
i
)
=
1
k
(
r
k
+
(
k
−
1
)
Q
k
−
1
)
=
1
k
(
r
k
+
k
Q
k
−
1
−
Q
k
−
1
)
=
Q
k
−
1
+
1
k
[
r
k
−
Q
k
−
1
]
\begin{aligned} Q_{k}& =\frac1k\sum_{i=1}^kr_i \\ &=\frac1k\left(r_k+\sum_{i=1}^{k-1}r_i\right) \\ &=\frac1k(r_k+(k-1)Q_{k-1}) \\ &=\frac1k(r_k+kQ_{k-1}-Q_{k-1}) \\ &=Q_{k-1}+\frac1k[r_k-Q_{k-1}] \end{aligned}
Qk=k1i=1∑kri=k1(rk+i=1∑k−1ri)=k1(rk+(k−1)Qk−1)=k1(rk+kQk−1−Qk−1)=Qk−1+k1[rk−Qk−1]
算法流程如下所示。
- 对于 ∀ a ∈ A \forall a \in A ∀a∈A,初始化计数器 N ( a ) = 0 N(a)=0 N(a)=0和期望奖励估计 Q ^ ( a ) = 0 \hat Q(a)=0 Q^(a)=0
- for t = i → T t = i \rightarrow T t=i→T do
- 基于策略 π \pi π,执行某个动作 a t a_t at
- 获得回报 r t = B a n d i t ( a t ) r_t=Bandit(a_t) rt=Bandit(at)
- 更新计数器 N ( a t ) = N ( a t ) + 1 N(a_t)=N(a_t)+1 N(at)=N(at)+1
- 更新期望奖励估值: Q ^ ( a t ) = Q ^ ( a t ) + 1 N ( a t ) [ r t − Q ^ ( a t ) ] \hat{Q}(a_t)=\hat{Q}(a_t)+\frac1{N(a_t)}\Big[r_t-\hat{Q}(a_t)\Big] Q^(at)=Q^(at)+N(at)1[rt−Q^(at)]
- end for
3.3. 懊悔regret函数
对于每一个动作,定义其期望收益 Q ( a i ) = E r ∼ R ( ⋅ ∣ a i ) [ r ∣ a i ] Q(a_i)=\mathbb{E}_{r\sim\mathcal{R}(\cdot|a_i)}\left[r|a_i\right] Q(ai)=Er∼R(⋅∣ai)[r∣ai]。
于是,至少存在一根拉杆,它的期望奖励不小于拉动其他任意一根拉杆,我们将该最优期望奖励表示为 Q ∗ = max a i ∈ A Q ( a i ) Q^*=\max_{a_i\in\mathcal{A}}Q(a_i) Q∗=maxai∈AQ(ai)
为了更加直观、方便地观察拉动一根拉杆的期望奖励离最优拉杆期望奖励的差距,我们引入懊悔(regret)概念。懊悔定义为拉动当前拉杆的动作 a a a与最优拉杆的期望奖励差,即 R ( a i ) = Q ∗ − Q ( a i ) R(a_i)=Q^*-Q(a_i) R(ai)=Q∗−Q(ai)
累积懊悔(cumulative regret)即操作 T T T次拉杆后累积的懊悔总量, σ R = ∑ t = 1 T R ( a t ) \sigma_R=\sum_{t=1}^TR(a_t) σR=∑t=1TR(at)
MAB 问题的目标为最大化累积奖励,等价于最小化累积懊悔。 min σ R = max E a ∼ π [ ∑ t = 1 T Q ( a t i ) ] \min\sigma_R=\max\mathbb{E}_{a\sim\pi}[\sum_{t=1}^TQ(a_t^i)] minσR=maxEa∼π[∑t=1TQ(ati)]
- 如果一直探索新策略: σ R ∝ T ⋅ R \sigma_R\propto T\cdot R σR∝T⋅R,累积懊悔将线性递增,无法收敛
- 如果一直不探索新策略: σ R ∝ T ⋅ R \sigma_R\propto T\cdot R σR∝T⋅R,累积懊悔将线性递增
因此需要考虑是否存在次线性的方式保证收敛。这里介绍一种由Lai&Robbinsti提出的方法:
使用
R
(
a
)
=
Q
∗
−
Q
(
a
)
R(a)=Q^*-Q(a)
R(a)=Q∗−Q(a)和反馈函数分布相似性:
D
K
L
(
R
(
r
∣
a
)
∥
R
⋆
(
r
∣
a
)
)
D_{KL}\bigl({\cal R}(r\mid a)\parallel{\cal R}^{\star}(r\mid a)\bigr)
DKL(R(r∣a)∥R⋆(r∣a))进行描述:
lim
T
→
∞
σ
R
≥
log
T
∑
a
∣
R
(
a
)
>
0
R
(
a
)
D
K
L
(
R
(
r
∣
a
)
∥
R
⋆
(
r
∣
a
)
)
\lim_{T\to\infty}\sigma_{R}\geq\log T\sum_{a|R(a)>0}\frac{R(a)}{D_{KL}\big(\mathcal{R}(r\mid a)\parallel\mathcal{R}^{\star}(r\mid a)\big)}
T→∞limσR≥logTa∣R(a)>0∑DKL(R(r∣a)∥R⋆(r∣a))R(a)
理论渐进最优收敛为
O
(
log
T
)
O(\log T)
O(logT)
反馈函数分布相似性
假设有两个反馈函数 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x),它们在区间 [ a , b ] [a,b] [a,b]上的密度函数分别为 p f ( x ) p_f(x) pf(x)和 p g ( x ) p_g(x) pg(x)。则可以使用Kullback-Leibler散度来描述它们之间的分布相似性,公式如下:
D K L ( p f ∣ ∣ p g ) = ∫ a b p f ( x ) log p f ( x ) p g ( x ) d x D_{KL}(p_f || p_g) = \int_a^b p_f(x) \log \frac{p_f(x)}{p_g(x)} dx DKL(pf∣∣pg)=∫abpf(x)logpg(x)pf(x)dx
其中, D K L ( p f ∣ ∣ p g ) D_{KL}(p_f || p_g) DKL(pf∣∣pg)表示 f ( x ) f(x) f(x)与 g ( x ) g(x) g(x)的分布差异,值越小表示两者分布越相似。
现在就来考虑采取什么样的策略 π \pi π,来使得收益最大化。
4. 贪心策略和 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略
对于贪心策略,每次都会选择最优的决策,显然这是一个利用Exploitation的过程。由前面的内容可知,累积懊悔是线性递增的。而
ϵ
−
g
r
e
e
d
y
\epsilon-greedy
ϵ−greedy策略,则是引入了噪声
ϵ
\epsilon
ϵ,以采样概率
1
−
ϵ
1-\epsilon
1−ϵ进行利用Exploitation(选择以往经验中期望奖励估值最大的那根拉杆),以采样概率
ϵ
\epsilon
ϵ进行探索 Exploration(随机选择一根拉杆)。公式如下:
a
t
=
{
arg
max
a
∈
A
Q
^
(
a
)
,
采样概率:1-
ϵ
从
A
中随机选择
,
采样概率:
ϵ
a_t=\begin{cases}\arg\max_{a\in\mathcal{A}}\hat{Q}(a),&\text{采样概率:1-}\epsilon\\\text{从 }\mathcal{A}\text{ 中随机选择},&\text{采样概率: }\epsilon&\end{cases}
at={argmaxa∈AQ^(a),从 A 中随机选择,采样概率:1-ϵ采样概率: ϵ
累积懊悔依旧是线性递增的,但是增长率要小。
衰减贪心策略
随着探索次数的不断增加,我们对各个动作的奖励估计得越来越准,此时我们就没必要继续花大力气进行探索。所以在 ϵ \epsilon ϵ -贪婪算法的具体实现中,我们可以令 ϵ \epsilon ϵ 随时间衰减,即探索的概率将会不断降低。但是请注意, ϵ \epsilon ϵ 不会在有限的步数内衰减至 0,因为基于有限步数观测的完全贪婪算法仍然是一个局部信息的贪婪算法,永远距离最优解有一个固定的差距。
一种可能的衰减策略:(一般难以找到合适的衰减策略)
c ≥ 0 , d = min a ∣ Δ a > 0 Δ a , ϵ t = min { 1 , c ∣ A ∣ d 2 t } c\geq0,\quad d=\min_{a|\Delta_a>0}\Delta_a,\quad\epsilon_t=\min\left\{1,\frac{c|\mathcal{A}|}{d^2t}\right\} c≥0,d=a∣Δa>0minΔa,ϵt=min{1,d2tc∣A∣}
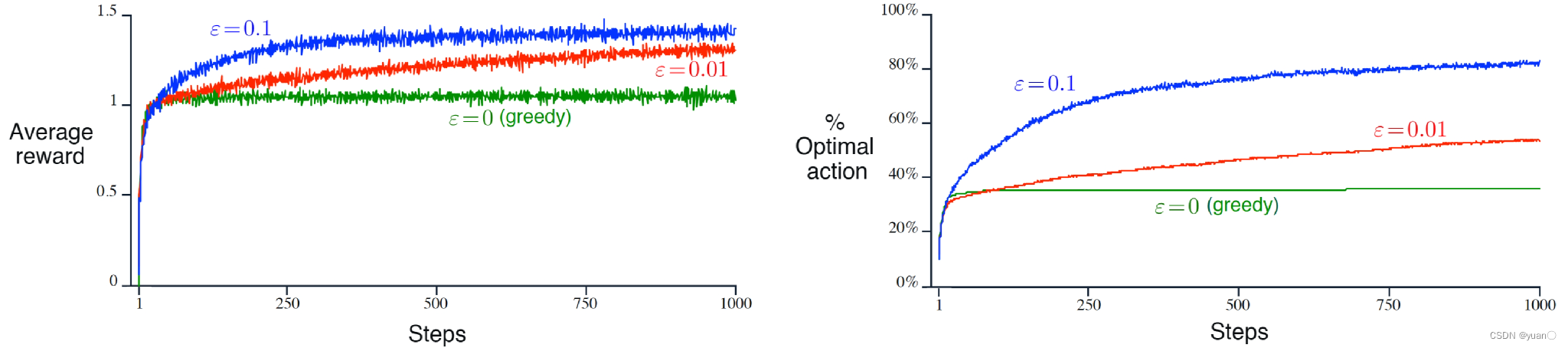
由上图可以看出,当 ϵ = 0 \epsilon=0 ϵ=0时,没有探索 Exploration的部分,只有利用Exploitation的部分,平均收益随着时间步长基本不变;当 ϵ = 0.1 \epsilon=0.1 ϵ=0.1时,增多了探索 Exploration的部分,开始时收益增长较大,之后保持一个较高的水平,并能够选择到更多的最优策略;当 ϵ = 0.01 \epsilon=0.01 ϵ=0.01时,则处于两者之间。
5. 积极初始化
给 Q ( a i ) Q(a_i) Q(ai)一个较高的初始值,同样采用增长式的更新方式。

- 是一种有偏估计,偏差的影响会随着采样的增多而减少
- 可能会陷入局部极小值。(调整 ϵ \epsilon ϵ)
6. 显示地考虑动作的价值分布

根据上面三个action的分布,如何进行选择?
- 鼓励不确定性
- 显示地根据分布采样进行选择
7. UCB上置信界算法
不确定性越大的 Q ( a i ) Q(a_i) Q(ai),越具有探索的价值。。我们在此引入不确定性度量 U ( a ) {U}(a) U(a),它会随着一个动作被尝试次数的增加而减小。我们可以使用一种基于不确定性的策略来综合考虑现有的期望奖励估值和不确定性,其核心问题是如何估计不确定性。
上置信界(upper confidence bound,UCB)算法是一种经典的基于不确定性的策略算法,它的思想用到了一个非常著名的数学原理:霍夫丁不等式(Hoeffding’s inequality)。
霍夫丁不等式是概率论中的一项重要不等式,它描述了大数定律的收敛速度。大致来说,霍夫丁不等式用于估计独立同分布随机变量之和的概率分布,这些随机变量的边界已知。它的表述如下:
设 X 1 , X 2 , . . . , X n X_1, X_2,...,X_n X1,X2,...,Xn是 n n n个独立同分布随机变量, 0 ≤ X i ≤ 1 0 \leq X_i \leq 1 0≤Xi≤1,其经验期望为 x ˉ n = 1 n ∑ j = 1 n X j \begin{aligned}\bar{x}_n=\frac{1}{n}\sum_{j=1}^nX_j\end{aligned} xˉn=n1j=1∑nXj,可得 P { E [ X ] ≥ x ˉ n + u } ≤ e − 2 n u 2 \mathbb{P}\left\{\mathbb{E}\left[X\right]\geq\bar{x}_n+u\right\}\leq e^{-2nu^2} P{E[X]≥xˉn+u}≤e−2nu2
现在我们将霍夫丁不等式运用于多臂老虎机问题中。将 Q ^ t ( a ) \hat Q_t(a) Q^t(a)代入 x ˉ t \bar{x}_t xˉt,不等式中的参数 u = U ^ t ( a ) u=\hat U_t(a) u=U^t(a)代表不确定性度量。给定一个概率 p = e − 2 N t ( a ) U t ( a ) 2 p=e^{-2N_t(a)U_t(a)^2} p=e−2Nt(a)Ut(a)2,根据上述不等式, Q t ( a ) < Q ^ t ( a ) + U ^ t ( a ) Q_t(a)<\hat Q_t(a)+\hat U_t(a) Qt(a)<Q^t(a)+U^t(a)至少以 1 − p 1-p 1−p的概率存在,若 p p p很小,则 Q t ( a ) < Q ^ t ( a ) + U ^ t ( a ) Q_t(a)<\hat Q_t(a)+\hat U_t(a) Qt(a)<Q^t(a)+U^t(a)存在的概率会很大, Q ^ t ( a ) + U ^ t ( a ) \hat Q_t(a)+\hat U_t(a) Q^t(a)+U^t(a)便是期望奖励的上界。
此时,上置信界算法便选取期望奖励上界最大的动作,即 a = arg max a ∈ A Q ^ ( a ) + U ^ ( a ) a=\arg\max_{a\in\mathcal{A}}\widehat{Q}(a)+\widehat{U}(a) a=argmaxa∈AQ (a)+U (a)。其中 U ^ t ( a ) = − log p 2 N t ( a ) \hat U_t(a)=\sqrt{\frac{-\log p}{2N_t(a)}} U^t(a)=2Nt(a)−logp.
因此,设定一个概率 p p p后,就可以计算相应的不确定性度量了。更直观地说,UCB 算法在每次选择拉杆前,先估计每根拉杆的期望奖励的上界 U ^ t ( a ) \hat U_t(a) U^t(a),使得拉动每根拉杆的期望奖励只有一个较小的概率 p p p超过这个上界,接着选出期望奖励上界最大的拉杆,从而选择最有可能获得最大期望奖励的拉杆。
或者采用这样的表示形式: A t ≐ arg max a [ Q t ( a ) + c ln t N t ( a ) ] A_t\doteq\arg\max_a\left[Q_t(a)+c\sqrt{\frac{\ln t}{N_t(a)}}\right] At≐argamax[Qt(a)+cNt(a)lnt]

可以看到,除了前面几步外, U C B UCB UCB之后的平均收益比 ϵ − g r e e d y \epsilon-greedy ϵ−greedy高
8. 汤普森采样算法
- 根据每个动作成为最优的概率来选择动作
数学表达:
p
(
a
)
=
∫
I
[
E
p
(
Q
(
a
)
)
[
Q
(
a
;
θ
)
]
=
max
a
′
∈
A
E
p
(
Q
(
a
′
)
)
(
Q
(
a
′
;
θ
)
)
]
d
θ
p(a)=\int\mathbb{I}\left[\mathbb{E}_{p(Q(a))}\left[Q(a;\theta)\right]=\max_{a'\in\mathcal{A}}\mathbb{E}_{p(Q(a'))}(Q(a';\theta))\right]d\theta
p(a)=∫I[Ep(Q(a))[Q(a;θ)]=a′∈AmaxEp(Q(a′))(Q(a′;θ))]dθ

汤普森采样(Thompson sampling)使用采样的方式,即根据当前每个动作 的奖励概率分布
p
(
Q
(
a
i
)
)
p(Q(a_i))
p(Q(ai))进行一轮采样,得到一组各根拉杆的奖励样本
Q
(
a
i
)
Q(a_i)
Q(ai),再选择样本中奖励最大的动作
a
a
a。可以看出,汤普森采样是一种计算所有拉杆的最高奖励概率的蒙特卡洛采样方法。

了解了汤普森采样算法的基本思路后,我们需要解决另一个问题:怎样得到当前每个动作
a
a
a的奖励概率分布并且在过程中进行更新?在实际情况中,我们通常用 Beta 分布对当前每个动作的奖励概率分布进行建模。具体来说,若某拉杆被选择了
k
k
k次,其中
m
1
m_1
m1次奖励为1,
m
2
m_2
m2次奖励为 0,则该拉杆的奖励服从参数为
(
m
1
+
1
,
m
2
+
1
)
(m_1+1,m_2+1)
(m1+1,m2+1) 的 Beta 分布。

Beta分布是一种概率分布,它的取值范围在0到1之间。它可以用于描述随机事件的概率,在统计学、机器学习、贝叶斯推断等领域中应用广泛。
Beta分布的概率密度函数如下:
f ( x ; α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x;\alpha,\beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha-1} (1-x)^{\beta-1} f(x;α,β)=B(α,β)1xα−1(1−x)β−1
其中, x x x表示随机变量的取值, α \alpha α和 β \beta β是分布的参数, B ( α , β ) B(\alpha, \beta) B(α,β)是Beta函数,定义为:
B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) B(\alpha, \beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)} B(α,β)=Γ(α+β)Γ(α)Γ(β)
其中, Γ \Gamma Γ是伽玛函数。
Beta分布的形状由参数 α \alpha α和 β \beta β决定。当 α = β = 1 \alpha=\beta=1 α=β=1时,Beta分布退化成均匀分布;当 α > 1 \alpha>1 α>1且 β > 1 \beta>1 β>1时,Beta分布具有单峰、钟形分布的形态;当 α < 1 \alpha<1 α<1或 β < 1 \beta<1 β<1时,Beta分布具有偏态分布的形态。Beta分布的期望为 α α + β \frac{\alpha}{\alpha+\beta} α+βα,方差为 α β ( α + β ) 2 ( α + β + 1 ) \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)} (α+β)2(α+β+1)αβ。
总结
- 探索 Exploration和利用 Exploitation是强化学习试错型学习(trial-and-error)中不可少的一部分;
- 多臂老虎机问题与强化学习的一大区别在于其与环境的交互并不会改变环境,即多臂老虎机的每次交互的结果和以往的动作无关,所以可看作无状态的强化学习(stateless reinforcement learning)
- 多臂老虎机是研究探索和利用理论的最佳环境(理论渐进最优收敛为 O ( log T ) O(\log T) O(logT));
- 各类探索和利用方法在RL,特别是在多臂老虎机中常用。
参考
[1] 伯禹AI
[2] https://www.deepmind.com/learning-resources/introduction-to-reinforcement-learning-with-david-silver
[3] 动手学强化学习
[4] Reinforcement Learning
[5] A Tutorial on Thompson Sampling https://web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf
[6] An Empirical Evaluation of Thompson Sampling




![web:[ACTF2020 新生赛]Include](https://img-blog.csdnimg.cn/823d78c0e209441b9e2eb0c0d27a7b70.png)