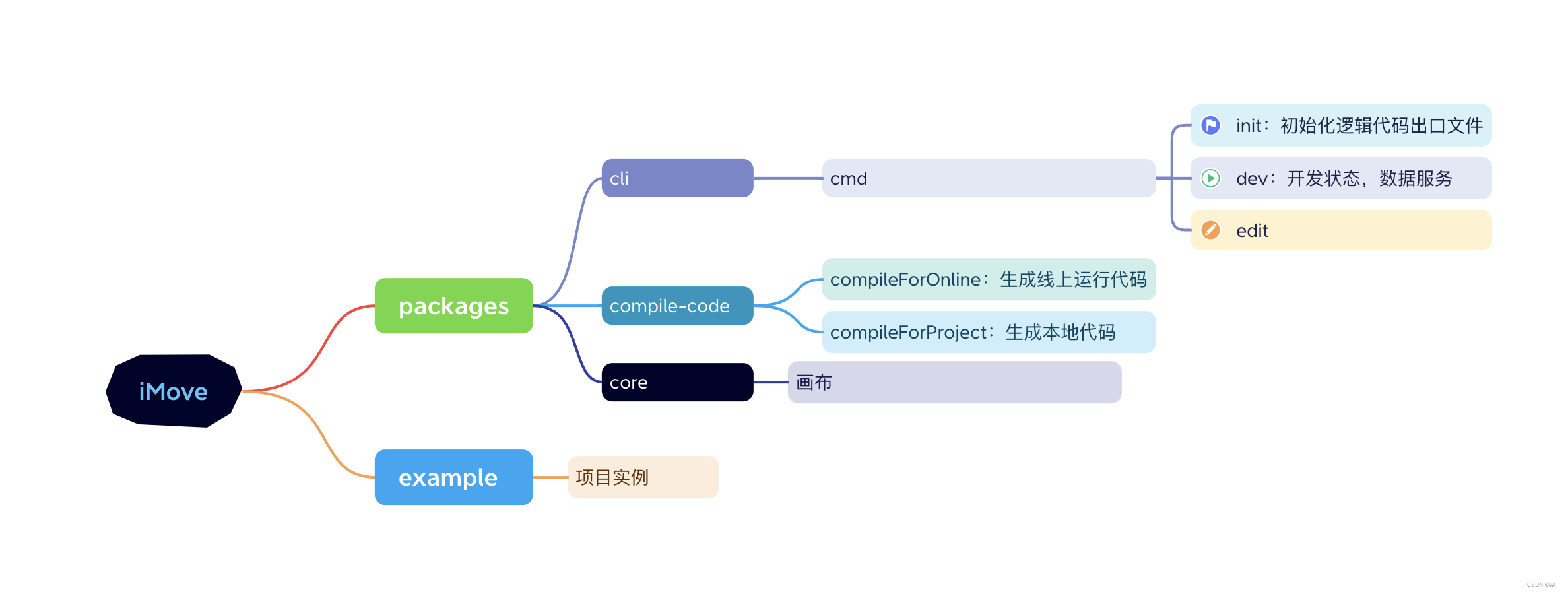
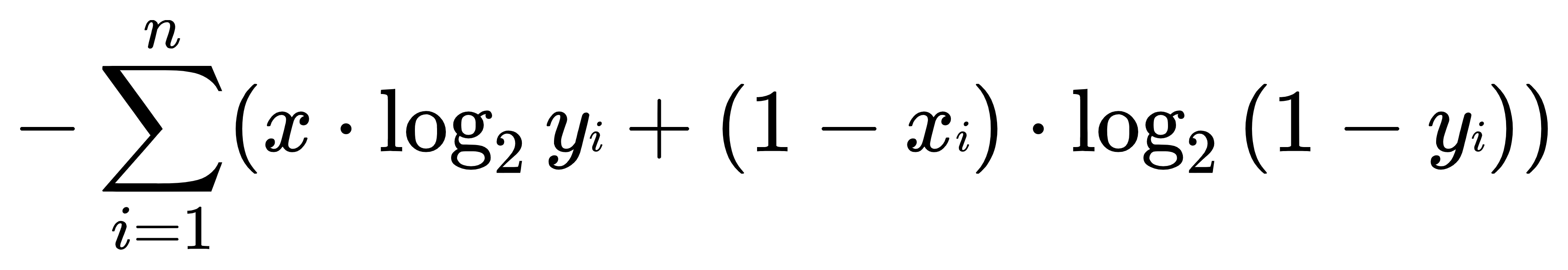最初的需求
需求是处理一些数据,数据例子:

而界面要显示的样子:

看起来不太难,可以分解出需求:
- 每一列的所有数据要都能参与选择,或者输入
- 当一个参数选中之后,比如选中A选中1,则B的选项范围只有3,4,5,6,7;C则只能输入1~16中的一个数
需求很清楚,需要行和列一一对应。简单的过滤就可以了。
需求开始变态
这是后业务说又有些新数据加入进来,他们长这样:

新加入的D参数有些类似C,但是又有点不一样,D依赖于A,不再是单纯的行对应,这里需要计算。
当然也可以解决,D的初始值,可以根据A的最大值求出来,然后选择的时候,再根据实时的值,实时计算。
接着变态
业务又加了参数:

新加的参数E是一个条件式的数据,它依赖于B的值。
不过也可以搞,变成表达式:
0<=B<5&&E<=C;5<=B<=16&&E<=C-2;B>16&&E<=C-5
分号表示或者,&&表示并且。计算初始值时,根据B的值找到C的最大值,然后得到E的最大值,然后取并集,得到所有可能范围,这个范围可能是不连续的多个区间。实时选择时,根据已选中的值,再次计算,仍然可以得到可选的范围。
进一步变态
业务又加了三个参数:

F在选择是是不显示的,G和H是要显示的,但是G和H的和要满足G+H<=F。
这个也可以搞,这个比上面的依赖繁琐一点,多个循环依赖,要检测。
这里所有参数都有个默认规则,就是肯定是大于等于0的。
检测的循环的时候,就把其中一个当0处理,然后求一个一元一次方程,根据定义域得到值域。实时选择时,仍然如此。
没有最变态,只有更变态
业务遇到新的数据:

一次添加了IJKLMNO。
以为只是复刻了前面的参数,当然还有要求。
I的值是JKL
- 当I选择J的时候,右侧参数只能有J和M
- 当I选择K的时候,右侧参数只能有K和N
- 当I选择L的时候,右侧参数只能有L和O
O还依赖G。
本来是想重新规划参数,加一下互斥组什么的,业务说我就不,我就要在原有的数据格式上录入。
没办法,最后折中
业务想录成这种:

当然这这三条,实际数据业务录入了1000条,头皮发麻。
硬着头皮搞了,支持参数值为无,当只有无时,不显示这参数。
实际的变态
有超级多的表格,每个表格的参数名字不相同,顺序也不同,值的格式也不同,依赖的参数是多个。
选择的时候要联动更新依赖这个参数的选框,不仅更新值,还要更新范围,更新选项。
做了好久,差不多做完了,使用了math.js和algebra.js前端库
没错,计算是在前端计算的。
https://mathjs.org/index.html
http://algebra.js.org/
- 使用math.js来计算表达式的值
- 使用algebra来求方程的解。