一、前言
本题基于leetcode155最小栈这道题,说一下通过java解决的一些方法。
需要尤其注意的是,此题输入的值的区间范围在-2^31 <= val <= 2^31 - 1.这将会影响我们最后一种最优解的结果出现问题。这些都是后话。
二、解决思路
其实在一开始的提交记录,我的方案忽略了题干中的常数时间,而是使用了偏向于工程的,将栈的所有元素放到数组中,然后通过数组的stream流的min方法解决:
class MinStack {
private Stack<Integer> stack;
public MinStack() {
stack = new Stack<>();
}
public void push(int val) {
stack.push(val);
}
public void pop() {
stack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
ArrayList<Integer> arrayList = new ArrayList<>();
arrayList.addAll(stack.subList(0, stack.size()));
return arrayList.stream().min(Integer::compare).get();
}
}
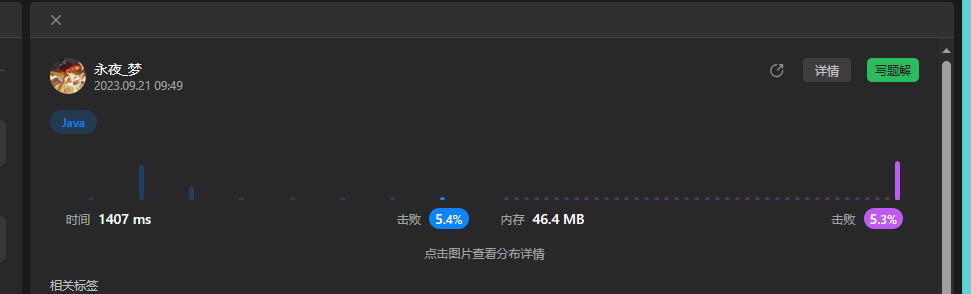
那么实际上stream也是一个循环,但是结果过了,可能并没有对时间去做一个检测。但是这个解决方案时间复杂度和空间复杂度均为O(n),是最拉的方案。所以这里完全不推荐。那么下面我们说一下一些比较OK的正解
2.1、辅助栈
这也是最容易想到的一种解决方案,我们定义一个辅助栈。当栈为空的时候,对于主栈和辅助栈都存放该元素。如果不为空,每次push的时候,通过将当前要插入的元素和辅助栈的栈顶元素去做一个对比,如果要插入的元素比栈顶元素小,则push要插入的元素,反之push辅助栈的栈顶元素。这样我们可以保证我们的辅助栈的栈顶一定对应的最小值,而出栈查看栈顶判空都很简单:出栈两个栈都需要pop,查看栈顶返回我们主栈的栈顶元素,查看最小值返回我们辅助栈的栈顶元素即可。
class MinStack {
private Stack<Integer> stack;
private Stack<Integer> assistStack;
public MinStack() {
stack = new Stack<>();
assistStack = new Stack<>();
}
public void push(int val) {
if(stack.isEmpty()){
stack.push(val);
assistStack.push(val);
}else {
stack.push(val);
assistStack.push(Math.min(assistStack.peek(), val));
}
}
public void pop() {
stack.pop();
assistStack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return assistStack.peek();
}
}
2.2、链表
我们可以通过自定义链表的方式,去定义一个节点,节点中增加一个属性min记录最小值,然后每次push的时候,类似链表的增加元素,而对于新的Node节点的min属性,思路很像上面辅助栈的思路,用要插入的值和head节点(其实就类似栈顶元素)的min做一个对比,如果要比min还小,则这个新节点的min就是要插入的值,反之是head节点的min.然后剩下的就是链表实现栈的常规操作了。代码如下:
class MinStack {
private Node head;
public void push(int x) {
if(head == null)
head = new Node(x, x);
else
//用当前要插入的值和头结点的最小值做一个对比
head = new Node(x, Math.min(x, head.min), head);
}
public void pop() {
head = head.next;
}
public int top() {
return head.val;
}
public int getMin() {
return head.min;
}
private class Node {
int val;
int min;
Node next;
private Node(int val, int min) {
this(val, min, null);
}
private Node(int val, int min, Node next) {
this.val = val;
this.min = min;
this.next = next;
}
}
}
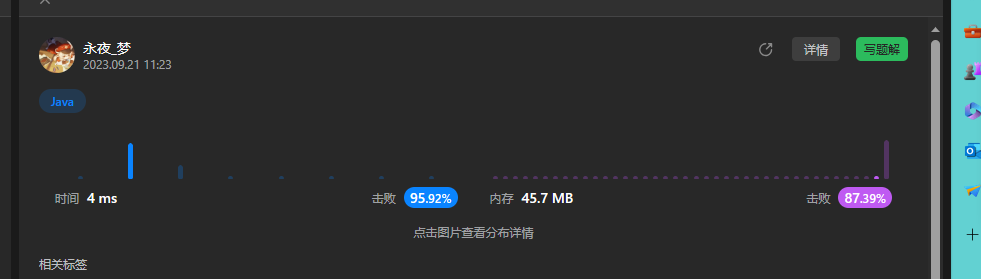
上面两个思路都差不多,所以最终的解决时间空间也都差不多,时间复杂度是O(1),空间复杂度为O(n)
2.3、存差值
那有没有时间复杂度和空间复杂度均为O(1)的解决方案呢,其实是有的。
我们可以额外存储一个值记录当前最小值min,然后我们的栈不放常规元素了。放差值,这个差值就是要插入元素x和我记录的最小值min的差值。记diff = x-min,这样对于getMin()操作我就可以直接返回记录的min了
对于push操作
当栈为空栈时,此时min就是要插入的值,diff记为0,所以push(0),记min = x;
当栈不为空,此时计算diff
如果diff >= 0; 那么说明要插入的值>=最小值,此时我们push(diff),但是我的min是不需要变动的
如果diff < 0:那么说明要插入的值<最小值,此时push(diff),但是我们记录min = x;
对于pop操作
由于我的最小值是一直在变动的,所以我们仍然需要查看栈顶即diff的值
如果diff<0的出栈了,这说明此时我的一个最小值出栈了,那么此时我需要变动我的min为min = min-diff
例如我的diff = -1,我的min记录此时为-3,那么我的min应该变成-3-(-1) = -2;
如果diff >=0的出栈,那就出栈,不用变动
对于top操作:
主要在于还原值
此时查看栈顶的diff值
如果diff<0,那么肯定当前栈顶的元素就是最小值,那么直接返回最小值min即可
如果diff>0,那么说明原来的元素要比最小值大diff,所以我应该返回min+diff;
那么代码如下:
class MinStack {
private Stack<Integer> stack;
private Integer min;
public MinStack(){
stack = new Stack<>();
min = 0;
}
public void push(int x) {
if(stack.isEmpty()){
//一开始由于栈是空栈,所以我们放入0.diff=0
stack.push(0);
min = x;
}else {
//不为空时,我们存插入的值和最小值的差值
int diff = x - min;
stack.push(diff);
//如果差值<0,说明要插入的比当前最小值还要小,此时更新最小值
if(diff < 0){
min = x;
}
}
}
public void pop() {
Integer pop = stack.pop();
//如果
if(pop < 0){
min = min - pop;
}
}
public int top() {
Integer diff = stack.peek();
if(diff < 0){
return min;
}else {
return min + diff;
}
}
public int getMin() {
return min;
}
}
但是需要注意的是:如果没有进行数值范围限制,上面的方法能行吗?答是不行,因为数值没有限制的话,差值的计算可能会溢出。例如Leetcode本题就无法用这个方法,因为这个方法一开始的数值范围是-2^31 <= val <= 2^31 - 1.那么在pop计算min-diff会出现下面的一幕,:
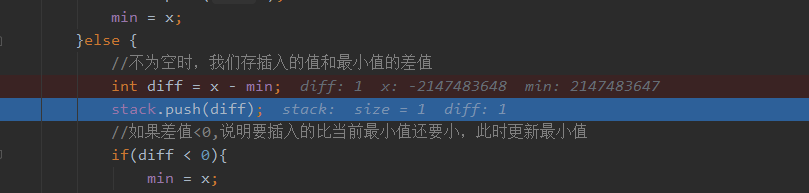
不过我们需要掌握这种思路,这种思路的时空复杂度均为O(1).也是最小栈的最优解