cp

一种常见套路（也是广义线段树问题的核心解决方法，UNR1好像也有一题）：

如果在线段树上进行一段区间修改，那么必然是一段右节点+一段左节点

这个过程其实就是zkw的本质

下面都要用zkw来理解

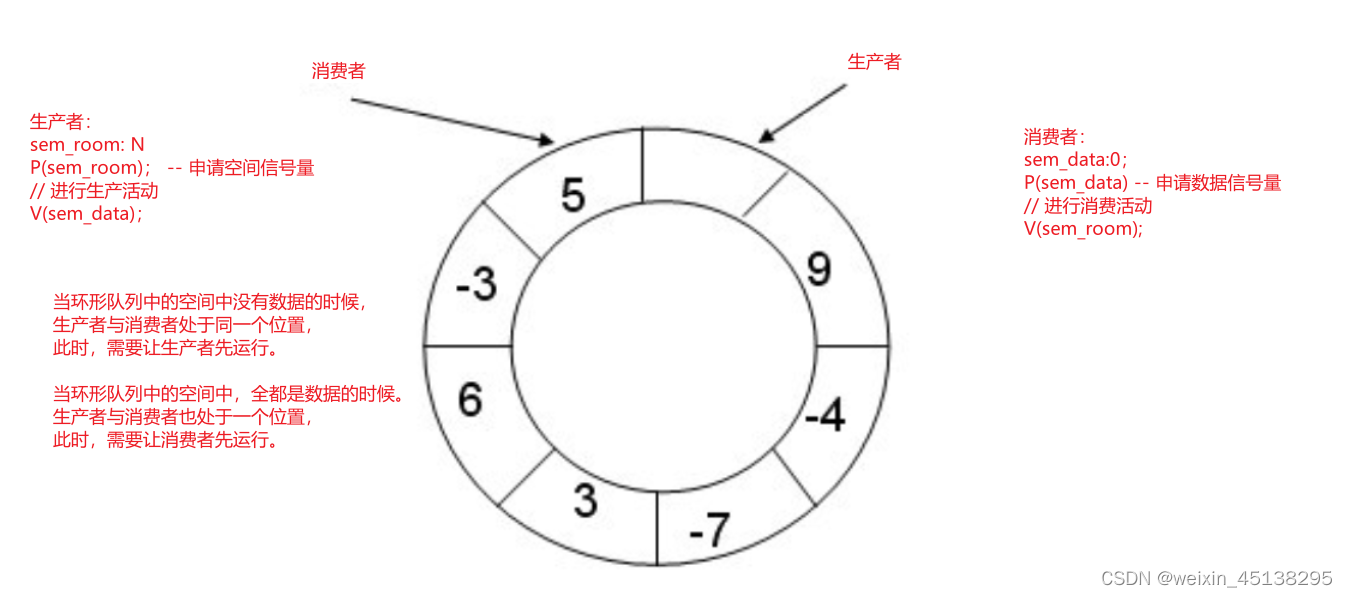
考虑原题，有一棵不规则的线段树

类似zkw，在这类题目中，我们要先把开区间变成闭区间

然后每个点记录其兄弟节点的信息

考虑现在区间为 $(x,y)$，我们可以先求出其 $z=lca(x,y)$

则 $x$ 要跳到 $ls[z]$，$y$ 要跳到 $rs[z]$

$x$ 在跳的过程中，如果它是左节点那么就修改/统计它的右节点

我们可以回顾zkw的过程帮助理解：

然后现在考虑优化跳的这个过程。

我们发现这就是个树剖。

然后就完成啦

时间复杂度 $O(n{\log }^{2}n)$

线段树套线段树

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back

#define N 400010
int n, m, i, j, k, T;
int f[N][22], q, x, y, ans, dep[N], lxy, op, d, mp[N]; 

struct Segment_tree {
	int tot, ls[N<<1], rs[N<<1], rt; 
	int s[N<<1], tag[N<<1], len[N<<1]; 
	void build(int &k, int l, int r) {
		if(!k) k=++tot; 
		if(l==r) return ; 
		int mid=(l+r)>>1; 
		build(ls[k], l, mid); 
		build(rs[k], mid+1, r); 
	}
	void make(int k, int l, int r, int x, int y) {
		if(l==r) return len[k]=y, void(); 
		int mid=(l+r)>>1; 
		if(x<=mid) make(ls[k], l, mid, x, y); 
		else make(rs[k], mid+1, r, x, y); 
		len[k]=len[ls[k]]+len[rs[k]]; 
	}
	void add(int k, int l, int r, int x, int y, int z) {
		if(l>=x && r<=y) {
			tag[k]+=z; s[k]+=len[k]*z; 
			return ; 
		}
		tag[ls[k]]+=tag[k]; s[ls[k]]+=len[ls[k]]*tag[k]; 
		tag[rs[k]]+=tag[k]; s[rs[k]]+=len[rs[k]]*tag[k]; 
		tag[k]=0; 
		int mid=(l+r)>>1;  
		if(x<=mid) add(ls[k], l, mid, x, y, z); 
		if(y>=mid+1) add(rs[k], mid+1, r, x, y, z); 
		s[k]=s[ls[k]]+s[rs[k]]; 
	}
	int que(int k, int l, int r, int x, int y) {
		if(l>=x && r<=y) return s[k]; 
		int mid=(l+r)>>1, sum=0; 
		tag[ls[k]]+=tag[k]; s[ls[k]]+=len[ls[k]]*tag[k]; 
		tag[rs[k]]+=tag[k]; s[rs[k]]+=len[rs[k]]*tag[k]; 
		tag[k]=0; 
		if(x<=mid) sum+=que(ls[k], l, mid, x, y); 
		if(y>=mid+1) sum+=que(rs[k], mid+1, r, x, y); 
		return sum; 
	}
}S1, S2;

struct Tree_chain_pou_score {
	int ls[N], rs[N], tot; 
	int w[N], st[N], ed[N], len[N]; 
	int up[N], dfn[N], p[N]; 
	int son[N], ltson[N]; 
	void dfs1(int x) {
		if(x<=n) {
			st[x]=ed[x]=x; w[x]=1; 
			return ; 
		}
		f[ls[x]][0]=f[rs[x]][0]=x; 
		dep[ls[x]]=dep[rs[x]]=dep[x]+1; 
		dfs1(ls[x]); dfs1(rs[x]); 
		st[x]=st[ls[x]]; ed[x]=ed[rs[x]]; 
		w[x]=w[ls[x]]+w[rs[x]]+1; 
	}
	void dfs2(int x, int Up) {
		up[x]=Up; dfn[x]=++tot; p[x]=tot;  
		len[x]=ed[x]-st[x]+1; 
		if(x<=n) return ; 
		if(w[ls[x]]>w[rs[x]]) son[x]=ls[x], ltson[x]=rs[x]; 
		else son[x]=rs[x], ltson[x]=ls[x]; 
		dfs2(son[x], Up); 
		dfs2(ltson[x], ltson[x]); 
		S1.make(1, 1, m, dfn[ls[x]], len[rs[x]]); 
		S2.make(1, 1, m, dfn[rs[x]], len[ls[x]]); 
	}
	void add(Segment_tree &Seg, int x, int y, int z) {
		while(up[x]!=up[y]) {
			Seg.add(1, 1, m, dfn[up[x]], dfn[x], z); 
			x=f[up[x]][0]; 
		}
		if(x==y) return ; 
		Seg.add(1, 1, m, dfn[y]+1, dfn[x], z); 
	}
	int que(Segment_tree &Seg, int x, int y) {
		int ans=0; 
		while(up[x]!=up[y]) {
			ans+=Seg.que(1, 1, m, dfn[up[x]], dfn[x]); 
			x=f[up[x]][0]; 
		}
		if(x==y) return ans; 
		ans+=Seg.que(1, 1, m, dfn[y]+1, dfn[x]); 
		return ans; 
	}
}Tree;

int lca(int x, int y) {
	if(x==y) return x; 
	if(dep[x]<dep[y]) swap(x, y); 
	for(int k=20; k>=0; --k)
		if(dep[f[x][k]]>=dep[y]) x=f[x][k]; 
	if(x==y) return x; 
	for(int k=20; k>=0; --k)
		if(f[x][k]!=f[y][k]) x=f[x][k], y=f[y][k]; 
	return f[x][0]; 
}

signed main()
{
	freopen("pigeons.in", "r", stdin);
	freopen("pigeons.out", "w", stdout);
	n=read(); q=read(); 
	for(i=n+1; i<2*n; ++i) {
		Tree.ls[i+2]=read(); Tree.rs[i+2]=read(); 
		if(Tree.ls[i+2]<=n) Tree.ls[i+2]++; 
		else Tree.ls[i+2]+=2; 
		if(Tree.rs[i+2]<=n) Tree.rs[i+2]++; 
		else Tree.rs[i+2]+=2; 
		mp[Tree.ls[i+2]]=mp[Tree.rs[i+2]]=1; 
	}
	for(i=n+3; mp[i]; ++i); 
	Tree.ls[2*n+2]=1; Tree.rs[2*n+2]=i; 
	Tree.ls[2*n+3]=2*n+2; Tree.rs[2*n+3]=n+2; 
	m=2*n+3; n=n+2; 
	dep[m]=1; Tree.dfs1(m); 
	S1.build(S1.rt, 1, m); S2.build(S2.rt, 1, m); 
	Tree.dfs2(m, m); 
	for(k=1; k<=20; ++k)
		for(i=1; i<=m; ++i) {
			f[i][k]=f[f[i][k-1]][k-1]; 
		}
	while(q--) {
		op=read(); 
		if(op==1) {
			x=read()+1; y=read()+1; d=read(); 
			lxy=lca(x-1, y+1); 
			Tree.add(S1, x-1, Tree.ls[lxy], d); 
			Tree.add(S2, y+1, Tree.rs[lxy], d); 
		}
		else {
			x=read()+1; y=read()+1; 
			lxy=lca(x-1, y+1); ans=0; 
			ans+=Tree.que(S1, x-1, Tree.ls[lxy]); 
			ans+=Tree.que(S2, y+1, Tree.rs[lxy]); 
			printf("%lld\n", ans); 
		}
	}
	return 0;
}