Problem - C - Codeforces

 

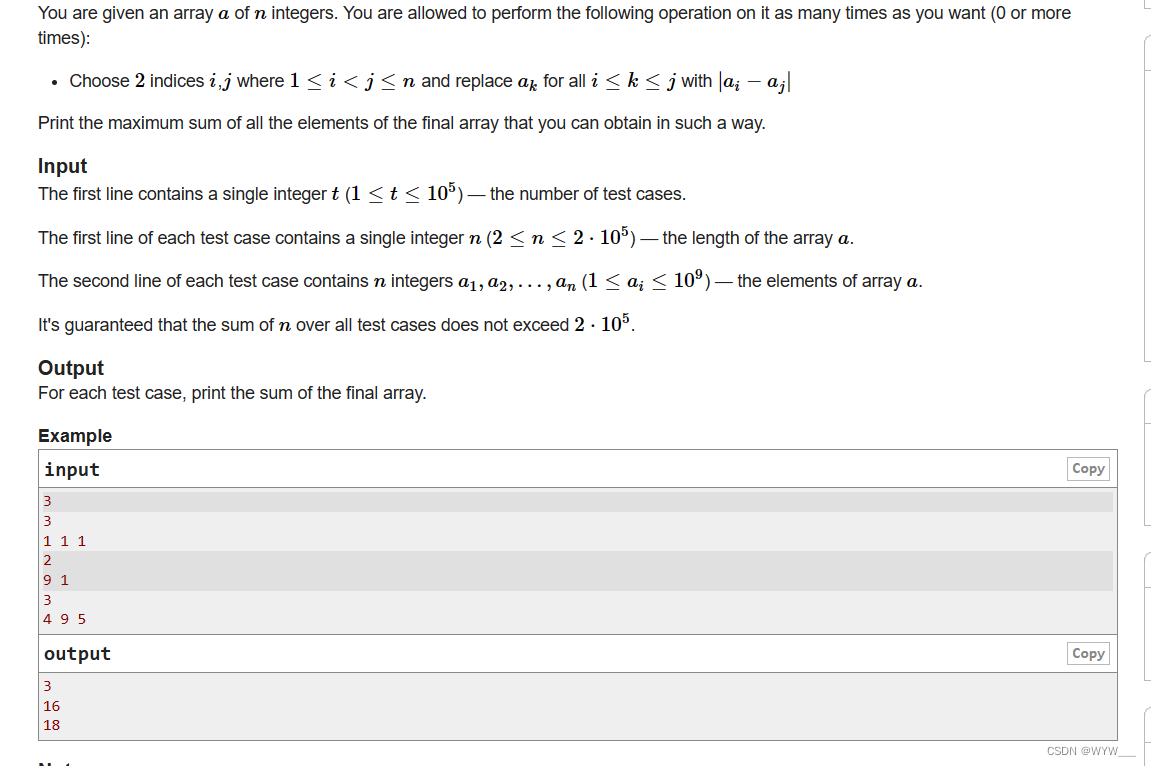
给你一个有n个整数的数组a。允许你对它进行以下操作，次数不限（0次或更多）。

选择2个指数i,j，其中1≤i<j≤n，用|ai-aj|替换所有i≤k≤j的ak。
打印最终数组中所有元素的最大和，你可以通过这种方式获得。

输入
第一行包含一个整数t（1≤t≤105）--测试案例的数量。

每个测试用例的第一行包含一个整数n(2≤n≤2⋅105)--数组a的长度。

每个测试用例的第二行包含n个整数a1,a2,...,an (1≤ai≤109) - 数组a的元素。

保证所有测试用例的n之和不超过2⋅105。

输出
对于每个测试用例，打印最终数组的总和。

例子
InputCopy
3
3
1 1 1
2
9 1
3
4 9 5
输出拷贝
3
16
18
注意
在第一个测试案例中，使用这些操作不可能达到大于3的和，因此最大和是3。

在第二个测试案例中，可以证明可实现的最大和是16。通过使用操作(1,2)，我们将数组从[9,1]转化为[8,8]，因此最终数组的和是16。

在第三个测试案例中，可以证明通过使用这些操作不可能实现大于18的和，因此最大和是18。

题解:
这题看过的人很少,想复杂了

其实我么可以发现如果n > 3时

类似

1 2 4 3 答案是是16

1 2

1 1 4 3

1 2

0 0 4 3

1 3

4 4 4 3

3 4

4 4 1 1

3 4

4 4 0 0

1 4

4 4 4 4

n >= 4都可以这样操作

剩下我们对前n <= 3进行分类讨论即可,主要是n = 3的情况

x y z

但其实也只有这几种情况

一种是x或z是最大*3

一种是abs(x-y)或abs(y-z)最大*3

一种是不变

#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
#include<set>
using namespace std;
#define int long long
int a[200050];
int b[200050];
void solve()
{
	int n;
	cin >> n;
	for(int i = 1;i <= n;i++)
	cin >> a[i];
	if(n == 1)
	{
		cout << a[1]<<"\n";
	}
	else if(n == 2)
	{
		cout << max(a[1]+a[2],2*abs(a[1]-a[2]))<<"\n";
	}
	else if(n == 3)
	{
		int ans = a[1]+a[2]+a[3];
		int f = max(max(a[3],a[1]),max(abs(a[3]-a[2]),abs(a[2]-a[1])));
		cout << max(ans,f*3)<<"\n";
	}
	else
	{
		sort(a+1,a+1+n);
		cout <<a[n]*n<<"\n";
	}
}
//101
signed main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int t = 1;
	cin >> t;
    while(t--)
	{
		solve();
	} 
}