朋友们、伙计们,我们又见面了,本期来给大家解读一下有关排序算法的相关知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成!
C 语 言 专 栏:C语言:从入门到精通
数据结构专栏:数据结构
个 人 主 页 :stackY、

目录
1.归并排序
1.1递归版本
代码演示:
1.2非递归版本
代码演示:
测试排序:
改正代码1:
测试排序:
改正代码2:
1.3递归版本的优化
代码演示:
2.归并排序特性
1.归并排序
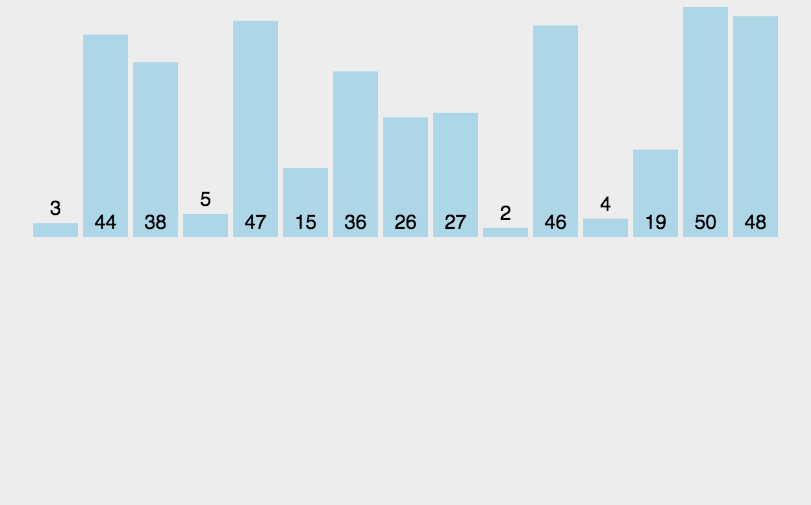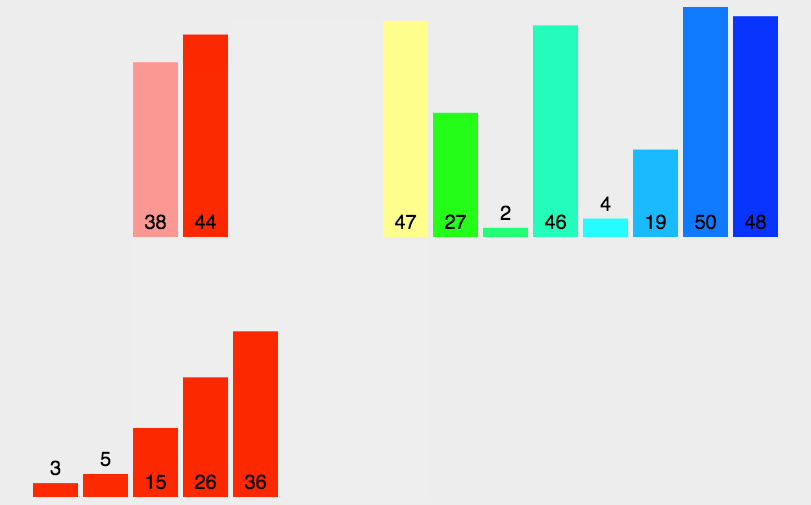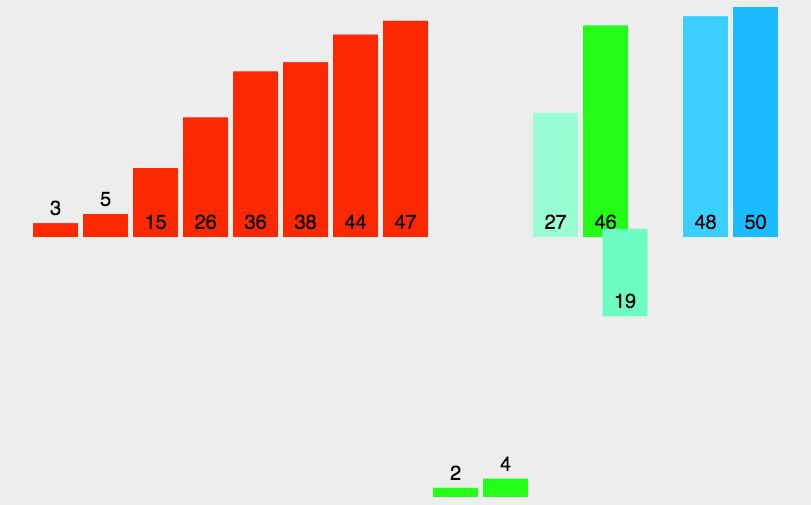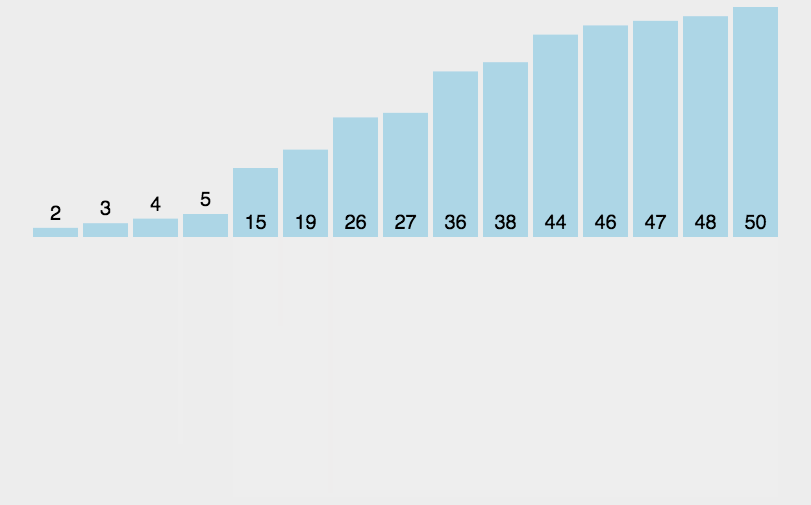
基本思想:归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤: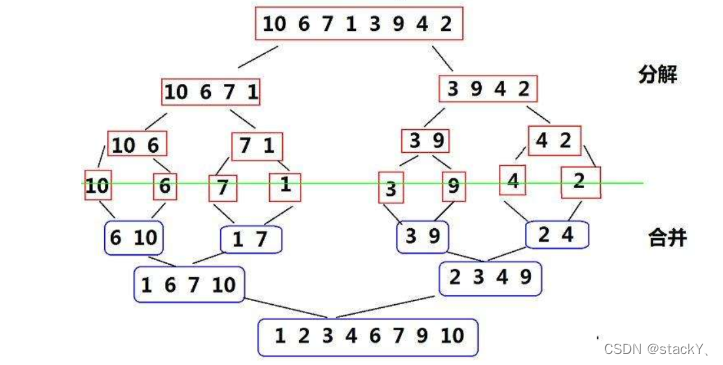
归并排序也分为递归和非递归版本,下面我们就来逐步学习:
1.1递归版本
从上面的图中我们可以看出归并排序是分为两个阶段分解和合并,那么转化为代码的思想就是先划分小区间,然后将区间中最小的单独拿出来在另外的一个数组中进行尾插,等到最后一组数据排完之后,再将尾插排序完的整个数组再拷贝至原数组,这样子就完成了整个数组的排序。
那么通过这个过程可以发现:归并排序是需要单独开一个数组的,所以它的
空间复杂度是O(N),另外归并排序是先划分小区间再进行排序,那么就和二叉树中的后序遍历逻辑类似,先将整个数据一分为二,使得左区间和右区间有序,然后再将左右两个区间进行排序,那么整个数据就有序了,所以需要让左右区间再有序,也需要将做右区间各划分为两个区间,并且让它们的左右区间再有序,以此类推,直到区间内只剩一个数据就不需要再划分了,然后取两个区间小的值尾插到单独的一个数组,最后再次整体拷贝至原数组。
在递归时要注意几个问题:
1. 在递归的时候需要保存两个区间的起始和终止位置,以便访问。
2. 当一个区间已经尾插完毕,那么直接将另外一个区间的数据依次尾插。
3. 两个区间的数据都尾插完毕至tmp数组时,需要将tmp数组的数据再次拷贝至原数组。
4. 在拷贝到原数组时需要注意尾插的哪一个区间就拷贝哪一个区间。
代码演示:
void _MergerSort(int* a, int begin, int end, int* tmp) { //递归截止条件 if (begin == end) return; //划分区间 int mid = (begin + end) / 2; //[begin,mid] [mid+1,end] //递归左右区间 _MergerSort(a, begin, mid, tmp); _MergerSort(a, mid + 1, end, tmp); //将区间保存 int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin; //取两个区间小的值尾插 //一个区间尾插完毕另一个区间直接尾插即可 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } //再将剩余数据依次尾插 //哪个区间还没有尾插就尾插哪一个 while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } //再重新拷贝至原数组 //尾插的哪个区间就将哪个区间拷贝 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergerSort(int* a, int n) { //先创建一个数组 int* tmp = (int*)malloc(sizeof(int) * n); _MergerSort(a, 0, n - 1, tmp); //释放 free(tmp); }
归并排序的特性总结:1. 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。2. 时间复杂度: O(N*logN)3. 空间复杂度: O(N)4. 稳定性:稳定
1.2非递归版本
由于递归代码在数据太多时可能会因为递归太深出现问题,所以我们也需要写出它们所对应的非递归版本的排序代码:非递归版本的归并排序直接可以使用循环来完成,但是坑点非常多,接下来我们就来慢慢排查。
我们可以先一个数据为一组,然后两两进行排序,然后将排序完的整体结果再重新拷贝至原数组,这样子就完成了一次排序,然后再将排序完的结果两个数据为一组,然后两两排序,然后将排序完的数据再拷贝至原数组,这样子就完成了第二次的排序,然后将数据四个分为一组,两两进行排序,再将排序完的数据拷贝至原数组,直到每组的数据超过或者等于数据的总长度即不需要在进行排序。
首先我们先创建一个开辟一个数组,然后设置一个gap用来分组,然后记录两个区间,对两个区间的数进行比较,小的尾插,再将剩余数据继续尾插,然后完成了一趟排序,再将排完序的数据再拷贝至原数组,再将gap * 2,继续完成剩余的排序,直到划分组的gap大于等于数据总长度即可完成全部的排序:
代码演示:
//归并排序 //非递归 void MergerSortNonR(int* a, int n) { //创建数组 int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("tmp"); exit(-1); } //划分组数 int gap = 1; while (gap < n) { int j = 0; for (int i = 0; i < n; i += 2 * gap) { //将区间保存 int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //取两个区间小的值尾插 //一个区间尾插完毕另一个区间直接尾插即可 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //再将剩余数据依次尾插 //哪个区间还没有尾插就尾插哪一个 while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } } //将数据重新拷贝至原数组 memcpy(a, tmp, sizeof(int) * n); //更新gap gap *= 2; } //释放 free(tmp); }测试排序:
void PrintArry(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ", a[i]); } printf("\n"); } void TestMergerSortNonR() { int a[] = { 10,6,7,1,3,9,4,2 }; PrintArry(a, sizeof(a) / sizeof(int)); MergerSortNonR(a, sizeof(a) / sizeof(int)); PrintArry(a, sizeof(a) / sizeof(int)); } int main() { TestMergerSortNonR(); return 0; }
可以看到排序完成,而且还完成的不错,那么我们再来几组数据进行测试:
在这里我们使用的是8个数据,那如果我们使用9个或者10个数据呢?
void PrintArry(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ", a[i]); } printf("\n"); } void TestMergerSortNonR() { int a[] = { 10,6,7,1,3,9,4,2,8,5 }; PrintArry(a, sizeof(a) / sizeof(int)); MergerSortNonR(a, sizeof(a) / sizeof(int)); PrintArry(a, sizeof(a) / sizeof(int)); } int main() { TestMergerSortNonR(); return 0; }
可以看到数据发生错误,那么到底是为什么呢?我们可以来一起观察一下:
随着gap的2倍递增,那么会发生数据区间越界的问题,因为当数据是10个的时候,gap会递增到8,因此在访问数据的时候会发生越界,我们也可以观察一下这个越界的现象:
可以将数据访问的区间打印出来:
那么该怎么解决这个问题呢?
1. 首先不能排完一次序然后将数据整体拷贝,需要排完一组,拷贝一组。
2. 其次当发生越界中的第一、二种时可以直接break。
3. 当发生越界中的第三种时可以将边界进行修正。
改正代码1:
//归并排序 //非递归 void MergerSortNonR(int* a, int n) { //创建数组 int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("tmp"); exit(-1); } //划分组数 int gap = 1; while (gap < n) { int j = 0; for (int i = 0; i < n; i += 2 * gap) { //将区间保存 int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //end1和begin2越界直接跳出 if (end1 >= n || begin2 >= n) { break; } //end2越界可以进行修正 if (end2 >= n) { end2 = n - 1; } //取两个区间小的值尾插 //一个区间尾插完毕另一个区间直接尾插即可 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //再将剩余数据依次尾插 //哪个区间还没有尾插就尾插哪一个 while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } //归并一组,拷贝一组 memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); } gap *= 2; } //释放 free(tmp); }测试排序:
void PrintArry(int* a, int n) { for (int i = 0; i < n; i++) { printf("%d ", a[i]); } printf("\n"); } void TestMergerSortNonR() { int a[] = { 10,6,7,1,3,9,4,2,8,5 }; PrintArry(a, sizeof(a) / sizeof(int)); MergerSortNonR(a, sizeof(a) / sizeof(int)); PrintArry(a, sizeof(a) / sizeof(int)); printf("\n"); int a2[] = { 10,6,7,1,3,9,4,2 }; PrintArry(a2, sizeof(a2) / sizeof(int)); MergerSortNonR(a2, sizeof(a2) / sizeof(int)); PrintArry(a2, sizeof(a2) / sizeof(int)); printf("\n"); int a3[] = { 10,6,7,1,3,9,4,2,8 }; PrintArry(a3, sizeof(a3) / sizeof(int)); MergerSortNonR(a3, sizeof(a3) / sizeof(int)); PrintArry(a3, sizeof(a3) / sizeof(int)); printf("\n"); } int main() { TestMergerSortNonR(); return 0; }
改正过后就完全的解决了越界的问题,那么这种改进方法是归并一组,拷贝一组。
我们也可以将全部越界的区间进行修正,然后排序完一次将整个数据拷贝。
改正代码2:
将越界区间全部修正也是可以达到改进的目的,我们就以归并数据的逻辑为基础,然后修改区间,因此需要将越界的区间改为不存在的区间即可:
//归并排序 //非递归 //改进代码2: void MergerSortNonR(int* a, int n) { //创建数组 int* tmp = (int*)malloc(sizeof(int) * n); //划分组数 int gap = 1; while (gap < n) { int j = 0; for (int i = 0; i < n; i += 2 * gap) { //将区间保存 int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; //将越界的区间修改为不存在的区间 if (end1 >= n) { end1 = n - 1; //修改为不存在的区间 begin2 = n; end2 = n - 1; } else if (begin2 >= n) { //不存在的区间 begin2 = n; end2 = n - 1; } else if (end2 >= n) { end2 = n - 1; } //取两个区间小的值尾插 //一个区间尾插完毕另一个区间直接尾插即可 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } //再将剩余数据依次尾插 //哪个区间还没有尾插就尾插哪一个 while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } } //整体拷贝 memcpy(a, tmp, sizeof(int) * n); gap *= 2; } //释放 free(tmp); }
1.3递归版本的优化
当数据量非常多的时候使用递归版本可以进行一个优化,当递归到小区间的时候,我们可以采用插入排序来进行优化,这个优化只限于递归版本,在进行小区间中的插入排序时需要注意在前面的步骤递归到了哪个区间就使用插入排序排序哪个区间,所以在进行插入排序的时候需要注意排序的区间。
代码演示:
void _MergerSort(int* a, int begin, int end, int* tmp) { //递归截止条件 if (begin == end) return; 小区间优化 //区间过小时直接使用插入排序,减少递归损耗 if (end - begin + 1 < 10) { // 注意排序的区间 InsertSort(a + begin, end - begin + 1); return; } //划分区间 int mid = (begin + end) / 2; //[begin,mid] [mid+1,end] //递归左右区间 _MergerSort(a, begin, mid, tmp); _MergerSort(a, mid + 1, end, tmp); //将区间保存 int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin; //取两个区间小的值尾插 //一个区间尾插完毕另一个区间直接尾插即可 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } //再将剩余数据依次尾插 //哪个区间还没有尾插就尾插哪一个 while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } //再重新拷贝至原数组 //尾插的哪个区间就将哪个区间拷贝 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } //归并排序 void MergerSort(int* a, int n) { //先创建一个数组 int* tmp = (int*)malloc(sizeof(int) * n); _MergerSort(a, 0, n - 1, tmp); //释放 free(tmp); }
2.归并排序特性
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。2. 时间复杂度:O(N*logN)3. 空间复杂度:O(N)4. 稳定性:稳定
朋友们、伙计们,美好的时光总是短暂的,我们本期的的分享就到此结束,最后看完别忘了留下你们弥足珍贵的三连喔,感谢大家的支持!