难度:1
1 二分查找返回关键值key在长度为len的数组arr[]中的位置,没有key则返回-1
int bi_search( int key, int arr[], int len )
//1 二分查找返回关键值key在长度为len的数组arr[]中的位置,没有key则返回-1
#include <iostream>
using namespace std;
int binSearch(int arr[], int len, int key)
{
int low = 0;
int high = len - 1;
int mid;
while(low <= high)
{
mid = (low+high)/2;
if(key == arr[mid]) return arr[mid];
else if(arr[mid]>key) high=mid-1;
else low=mid+1;
}
return -1;
}
int main(){
int arr[] = {1,2,3,4,5,6,7,8,9,10,11};
int key = 0;
printf("输入你要查找的数:\n");
scanf("%d",&key);
printf("查找的数 %d 在数组中的位置为:%d\n",key,binSearch(arr,sizeof(arr)/sizeof(arr[0]),key));
return 0;
}
执行效果:
2 实现指定整数的三种查询方法:
int linear_search( int arr[], int len, int key )
#include <iostream>
using namespace std;
int better_search(int arr[],int len,int key){
int i;
for(i=len-1;i>=0;i--){
if (arr[i]==key)
{
break;
}
}
return i;
}
int main(){
int n=10;
int arr[11]={0};
printf("输入长度为10 的数组:\n");
for(int i=0;i<n;i++){
scanf("%d",&arr[i]);
}
int key;
printf("输入要查找的数:\n");
scanf("%d",&key);
printf("要查找的数的位置为:%d",better_search(arr,sizeof(arr)/sizeof(arr[0]),key));
return 0;
}
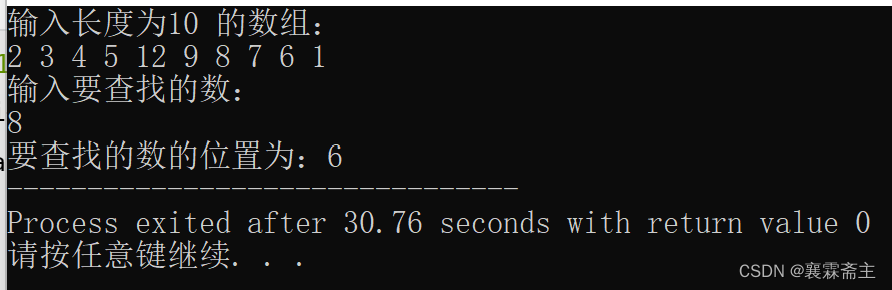
执行结果:
int better_search( int arr[], int len, int key )
#include <iostream>
using namespace std;
int linear_search(int arr[],int len,int key){
for(int i=0;i<len;i++){
if (arr[i]==key)
{
return i;
}
}
return -1;
}
int main(){
int n=10;
int arr[11]={0};
printf("输入长度为10 的数组:\n");
for(int i=0;i<n;i++){
scanf("%d",&arr[i]);
}
int key;
printf("输入要查找的数:\n");
scanf("%d",&key);
printf("要查找的数的位置为:%d",linear_search(arr,sizeof(arr)/sizeof(arr[0]),key));
return 0;
}
执行结果:
int sentinel_linear_search( int arr[], int len, int key )
#include <iostream>
using namespace std;
int search(int arr[ ], int n, int k)
{
int i = n;
arr[0] = k; //0位置空出来
while (arr[i] != k)//要么在1--n处找到,要么在0处出while循环
i--;
return i;
}
int main(){
int n=10;
int arr[11]={0};
printf("输入长度为10 的数组:\n");
for(int i=0;i<n;i++){
scanf("%d",&arr[i]);
}
int key;
printf("输入要查找的数:\n");
scanf("%d",&key);
printf("要查找的数的位置为:%d",search(arr,sizeof(arr)/sizeof(arr[0]),key));
return 0;
}
执行结果:
3 用递归的方法求解斐波那契数列第n项的值:
long fib( int n ) // 返回斐波那契数列第n项的值
#include <iostream>
using namespace std;
int f(int n){
if(n==1||n==2) return 1;
else{
return f(n-1)+f(n-2);
}
}
int main(){
printf("请输入要求第几个斐波那契数:\n");
int n;
scanf("%d",&n);
printf("第%d个斐波那契数的值为:%d",n,f(n));
return 0;
}
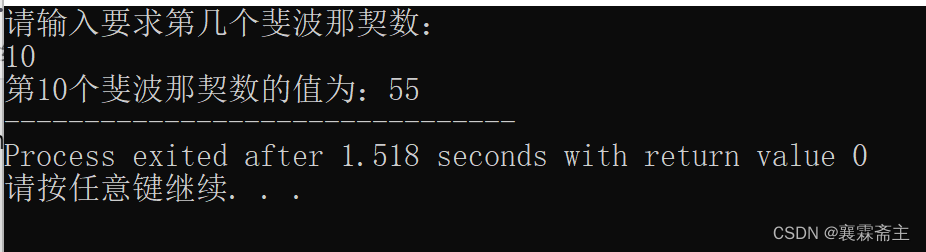
执行结果:
4 数组反转,给定长度为len的数组arr[],请将里面的元素反转,
如开始为{1,5,6,2,6,7,8} 反转后为{8,7,6,2,6,5,1}
void reverse( int arr[], int len )
int reverse(int arr[]){
int temp = 0;
int n = arr.size();
for(int i = 0; i< n/2; i++){
temp = arr[n-i-1];
arr[n-i-1] = arr[i];
arr[i] = temp;
}
return arr;
}
5 给定一个字符串,若里面含有相同的字母则返回1,否则返回0.
#include <iostream>
using namespace std;
int hashtable[1000];
int check(string a,int len){
for(int i=0;i<a.size();i++){
if(hashtable[a[i]]!=0) return 1;
hashtable[a[i]]=1;
}
return 0;
}
int main(){
string a;
getline(cin,a);
int len=a.length();
printf("%d",check(a,len));
}
难度:2
1 递归实现:二分查找返回关键值key在长度为len的数组arr[]中的位置,没有key则返回-1 int rec_bi_search( int key, int arr[], int low, int high )
#include <iostream>
using namespace std;
int binSearch(int arr[], int len, int key)
{
int low = 0;
int high = len - 1;
int mid;
while(low <= high)
{
mid = (low+high)/2;
if(key == arr[mid]) return arr[mid];
else if(arr[mid]>key) high=mid-1;
else low=mid+1;
}
return -1;
}
int main(){
int arr[] = {1,2,3,4,5,6,7,8,9,10,11};
int key = 0;
printf("输入你要查找的数:\n");
scanf("%d",&key);
printf("查找的数 %d 在数组中的位置为:%d\n",key,binSearch(arr,sizeof(arr)/sizeof(arr[0]),key));
return 0;
}
2 用优化递归方法,求解斐波那契数列第n项的值: long fib( int n, long result[], int len ) 返回斐波那契数列第n项的值,,result[i]存储第i项的值,len是result的长度。
动态规划法:把每一个计算出来的数据,用一个数组保存,需要最终值时直接从数组中取即可,避免重复计算。有一个for循环,其时间复杂度为O(n),开辟一个长度为n的数组,所以空间复杂度也为O(n)
1 public int fib(int n) {
2 int[] fib = new int[n];
3 fib[0] = 1;
4 fib[1] = 1;
5 for (int i = 2; i < n; i++) {
6 fib[i] = fib[i - 2] + fib[i - 1];
7 }
8 return fib[n - 1];
9 }
3 用选择排序的方法实现对整型数据由小到大进行排序 void select_sort( int arr[], int len ) arr为数组名,len为数组的长度。
#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
for (int i = 0; i < n; i++) {
// 寻找[i, n)区间里的最小值
int minIndex = i;
for (int j = i + 1; j < n; j++)
if (arr[j] < arr[minIndex])
minIndex = j;
swap(arr[i], arr[minIndex]);
}
}
void swap(int arr[], int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
int main(){
int arr[10] = {3,5,4,2,7,23,56,6,51,76};
selectionSort(arr,10);
for(int i=0;i<10;i++){
printf("%d ",arr[i]);
}
}
4 用插入排序的方法实现对整型数据由小到大进行排序 void insert_sort( int arr[], int len ) arr为数组名,len为数组的长度。
#include<iostream>
using namespace std;
int main() {
int a[6] = { 2, 6, 5, 3, 4, 1};
int temp, i, j;
int n = 6;
for (i = 1; i < 6; i++) { // 数组的下标是从0开始的
// 这里从第二个数开始枚举 即假定第一个数是有序的
temp = a[i]; j = i; // 这里temp 临时储存每一次需要排序的数
while (j >= 1 && temp < a[j - 1]) {
a[j] = a[j - 1];
j--;
}
a[j] = temp;
}
for (i = 0; i < 6; i++) {
cout << a[i] << " ";
}
cout << endl;
return 0;
}
难度:3
1 判断字符串中的括号是否正确匹配,如正确的匹配()、()[]{}、{[]}、{([])}、错误的匹配{)、{[)}等等 正确返回1,错误返回0
#include <iostream>
#include <cstring>
#include <stack>
using namespace std;
int main()
{
stack<char>a;
int flag=1,i;
char ch[100];
cin>>ch;
for(i=0;i<strlen(ch);i++){
if(ch[i]=='{'||ch[i]=='('||ch[i]=='[')
a.push(ch[i]);
else{
if(a.empty()==true){
flag=0;
break;
}
else if((ch[i]=='}'&&a.top()=='{')||(ch[i]==')'&&a.top()=='(')||(ch[i]==']'&&a.top()=='['))
a.pop();
else{
flag = 0;
break;
}
}
}
if(flag==0)
cout<<"no";
else
cout<<"yes";
}
2 用快速排序的方法实现对整型数据由小到大进行排序 void quick_sort( int arr[], int len )
//快速排序
#include <iostream>
using namespace std;
void QuickSort(int *array,int low,int high){ //快排
if(low>=high){ //若待排序序列只有一个元素,返回空
return ;
}
int i=low; //i作为指针从左向右扫描
int j=high; //j作为指针从右向左扫描
int key=array[low];//第一个数作为基准数
while(i<j){
while(array[j]>=key&&i<j){ //从右边找小于基准数的元素 (此处由于j值可能会变,所以仍需判断i是否小于j)
j--; //找不到则j减一
}
array[i]=array[j]; //找到则赋值
while(array[i]<=key&&i<j){ //从左边找大于基准数的元素
i++; //找不到则i加一
}
array[j]=array[i]; //找到则赋值
}
array[i]=key; //当i和j相遇,将基准元素赋值到指针i处
QuickSort(array,low,i-1); //i左边的序列继续递归调用快排
QuickSort(array,i+1,high); //i右边的序列继续递归调用快排
}
int main(){
int array[]={49,38,65,97,76,13,27,49};
int length=sizeof(array)/sizeof(*array);
cout<<"原始序列:";
for(int i=0;i<length;i++){
cout<<array[i]<<" ";
}
cout<<endl;
QuickSort(array,0,length-1);
cout<<"快排序列:";
for(int i=0;i<length;i++){
cout<<array[i]<<" ";
}
return 0;
}
3 给定长度为len的数组arr,打印出数组元素的所有排序。 如arr[4]={3,5,2,7},则输出这4个整数的24种排列形式
#include<iostream>
using namespace std;
//交换
void swap(int &a , int &b)
{
int temp;
temp = a;
a = b;
b = temp;
}
//全排列递归算法
void Perm(int list[] , int k ,int m)
{
//list 数组存放排列的数,K表示层 代表第几个数,m表示数组的长度
if(k==m)
{
//K==m 表示到达最后一个数,不能再交换,最终的排列的数需要输出;
for(int i=0 ;i<=m ;i++)
cout<<list[i];
cout<<endl;
}
else{
for(int i=k;i<=m;i++)
{
swap(list[i],list[k]);
Perm(list,k+1,m);
swap(list[i] , list[k]);
}
}
}
int main(void)
{
int a[]={1,2,3};
int m=2;
Perm(a,0,2);
}
4 字符串定位:返回字符串str,在字符串dest中出现的位置(第一个字母),没有出现则返回-1 int locate(char* str, char* dest) 例如 locate( “abc”, “fadbabdabcda”) 则返回7
滑动窗口
int slideToSubString_III(string str, string sub) {
int i = 0, j = 0;
int index = 0;
while (i < str.length() && j < sub.length()) {
if (str[i] == sub[j]) {
i++;
j++;
} else {
i = i - j + 1;
j = 0;
}
if (j == sub.length()) {
return i - j;
}
}
return 0;
}
难度:4
1 计算正确的四则整形运算表达式的值。输入一个正确四则整形运算表达式字符串,输出计算结果(除法可以直接执行整数除,不考虑小数,如5/4等于1)。如输入“(17+3)/4+2",输出7。
#include <iostream>
#include <string>
#include <stack>
#include <unordered_map>
using namespace std;
stack<char> op;
stack<int> num;
unordered_map<char, int> pr = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
void eval()
{
int b = num.top(); num.pop();
int a = num.top(); num.pop();
char c = op.top(); op.pop();
int x;
if(c == '+') x = a + b;
else if(c == '-') x = a - b;
else if(c == '*') x = a * b;
else x = a / b;
num.push(x);
}
int main()
{
string s;
cin >> s;
for(int i = 0; i < s.size(); i++)
{
char c = s[i];
if(isdigit(c))
{
int x = 0, j = i;
while(j < s.size() && isdigit(s[j])) x = 10 * x + s[j++] - '0';
i = j - 1;
num.push(x);
}
else if(c == '(') op.push(c);
else if(c == ')')
{
while(op.size() && op.top() != '(') eval();
op.pop();
}
else
{
while(op.size() && pr[op.top()] >= pr[c]) eval();
op.push(c);
}
}
while(op.size()) eval();
cout << num.top() << endl;
return 0;
}
2 对n个等长(长度为len)的字符串进行字典顺序排序 sort_str( char* str[], int len, int n )
#include <vector>
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
bool cmp(string a, string b)
{
return a < b;
}
int main()
{
int num;
string str;
vector<string> v;
while (cin >> num)
{
while (num--)
{
cin >> str;
v.push_back(str);
}
sort(v.begin(),v.end(),cmp);
cout << endl;
for (int i = 0; i < v.size(); i++)
{
cout << v[i] << endl;
}
}
return 0;
}
3 建立10个节点的有向图,由用户输入节点对来完成。由用户指定一个源点,输出所有与之连通的所有结点的最短路径及路径长度。
int graph[10][10];
int shortest[10];
int pred[10];
void create_graph( void )
void dijkstra( int source )
void show_shortest_path( int source )
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}
4 利用数组实现堆的三种基本操作, 插入元素:void insert( int x, int heap[], int len) 删除元素:int delete( int heap[], int len ) 更新元素:void update( int x, int pos, int heap[], int len ) x 为插入或新元素, heap为堆,len是堆的尺寸,pos是新元素的位置。
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int h[N]; //堆
int ph[N]; //存放第k个插入点的下标
int hp[N]; //存放堆中点的插入次序
int cur_size; //size 记录的是堆当前的数据多少
//这个交换过程其实有那么些绕 但关键是理解 如果hp[u]=k 则ph[k]=u 的映射关系
//之所以要进行这样的操作是因为 经过一系列操作 堆中的元素并不会保持原有的插入顺序
//从而我们需要对应到原先第K个堆中元素
//如果理解这个原理 那么就能明白其实三步交换的顺序是可以互换
//h,hp,ph之间两两存在映射关系 所以交换顺序的不同对结果并不会产生影响
void heap_swap(int u,int v)
{
swap(h[u],h[v]);
swap(hp[u],hp[v]);
swap(ph[hp[u]],ph[hp[v]]);
}
void down(int u)
{
int t=u;
if(u*2<=cur_size&&h[t]>h[u*2]) t=u*2;
if(u*2+1<=cur_size&&h[t]>h[u*2+1]) t=u*2+1;
if(u!=t)
{
heap_swap(u,t);
down(t);
}
}
void up(int u)
{
if(u/2>0&&h[u]<h[u/2])
{
heap_swap(u,u/2);
up(u>>1);
}
}
int main()
{
int n;
cin>>n;
int m=0; //m用来记录插入的数的个数
//注意m的意义与cur_size是不同的 cur_size是记录堆中当前数据的多少
//对应上文 m即是hp中应该存的值
while(n--)
{
string op;
int k,x;
cin>>op;
if(op=="I")
{
cin>>x;
m++;
h[++cur_size]=x;
ph[m]=cur_size;
hp[cur_size]=m;
//down(size);
up(cur_size);
}
else if(op=="PM") cout<<h[1]<<endl;
else if(op=="DM")
{
heap_swap(1,cur_size);
cur_size--;
down(1);
}
else if(op=="D")
{
cin>>k;
int u=ph[k]; //这里一定要用u=ph[k]保存第k个插入点的下标
heap_swap(u,cur_size); //因为在此处heap_swap操作后ph[k]的值已经发生
cur_size--; //如果在up,down操作中仍然使用ph[k]作为参数就会发生错误
up(u);
down(u);
}
else if(op=="C")
{
cin>>k>>x;
h[ph[k]]=x; //此处由于未涉及heap_swap操作且下面的up、down操作只会发生一个所以
down(ph[k]); //所以可直接传入ph[k]作为参数
up(ph[k]);
}
}
return 0;
}
5 输入一段文本,打印输出对应的哈夫曼编码: void hfm(char str[], int len)
6 建立6个节点的无向图。由用户指定一个源点、一个终点,输出从源点到终点的所有路径及长度。
7 在2行5列的格子中填入1到10的数字。要求:相邻的格子中的数,右边的大于左边的,下边的大于上边的。请你计算一共有多少种可能的方案,并输出所有的方案。
#include<stdio.h>
int a[2][5];
int cou = 0;
int flag[10];
int check()
{
if (a[1][0] < a[0][0])
return 0;
for (int i = 1; i < 5; i++)
{
if (a[0][i] < a[0][i-1])
{
return 0;
}
if (a[1][i] < a[1][i-1])
{
return 0;
}
if (a[1][i] < a[0][i])
{
return 0;
}
}
return 1;
}
void DFS(int num)
{
if (num == 10)
{
if (check())
{
cou++;
}
return;
}
for (int i = 1; i <= 10; i++)
{
if (flag[i] == 0)
{
flag[i] = 1;
a[num / 5][num % 5] = i;
DFS(num + 1);
flag[i] = 0;
}
}
}
int main()
{
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < 5; j++)
{
a[i][j] = 0;
}
}
for (int i = 0; i < 10; i++)
{
flag[i] = 0;
}
DFS(0);
printf("%d\n", cou);
}
难度:5
1 计算四则运算表达式的值。输入一个正确四则运算表达式字符串,表达式正确则输出计算结果,错误则给出提示。
在这里插入代码片
2 对n个不等长的字符串进行字典顺序排序,各字符串长度存放在数组len中 sort_str( char* str[], int len[], int n )
//这里我们引用了string.h库里的比较函数strcmp()和复制函数strpy()
#include<stdio.h>
#include<string.h>
int main()
{
char a[201][201];//首先我们建立一个存放输入字符串的二维数组
char b[201];//再建立一个临时存放字符串的数组
int n;
scanf("%d",&n);//n个字符串
for(int i=0;i<n;i++)
scanf("%s",a[i]);//实际上,二维数组的每一行存放一个字符串
for(int i=0;i<n;i++)//控制行数,从第一行开始
for(int j=i+1;j<n;j++)//从i的下一行开始
{
if(strcmp(a[i],a[j])>0)//不断比较前一个与后一个
{//如果前一个字符的ASCII码大于后一个则交换位置
//这个则由strcmp的值来反应,如果前一个元素大于后一个元素
//则返回值1,如果相等返回值0,如果小于,返回值-1
strcpy(b,a[i]);//利用临时数组存放字符串
strcpy(a[i],a[j]);//将括号里的第二个元素赋给第一个元素
strcpy(a[j],b);//结果是后一个与前一个交换
}
}
for(int i=0;i<n;i++)
{
printf("%s\n",a[i]);//将每一行的字符串打印出来
}
}
3 0-1背包问题。假设你有一个背包,最多能承重C千克,这里有k个物品,其重量分别为w1、w2、……、wk,在背包所能承受的重量下,尽可能得使背包里的物品重量最大。
void bag( int ball[], int n, int w)
//0-1背包问题
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int f[MAXN]; //
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++) {
int v, w;
cin >> v >> w; // 边输入边处理
for(int j = m; j >= v; j--)
f[j] = max(f[j], f[j - v] + w);
}
cout << f[m] << endl;
return 0;
}





![[附源码]Python计算机毕业设计Django医院挂号住院管理系统](https://img-blog.csdnimg.cn/083accd3d3dc45159022781972ecbac6.png)




![[附源码]计算机毕业设计Python的剧本杀管理系统(程序+源码+LW文档)](https://img-blog.csdnimg.cn/ec43f22b3ef04fd88f2f46ccc6db417e.png)