上课老师讲了Hashset的添加元素方法,感觉不甚准确,于是下课扒一扒底层源码,这一看,霍!
原来如此。现在小丁来捋一遍他的存储原理。
public boolean add(E e) {
return map.put(e, PRESENT)==null;
}可以看到PRESENT是一个private static final修饰的object对象
private static final Object PRESENT = new Object();首先它返回了一个map的put方法,并判断它是不是添加成功,添加成功返回true,反之返回false
继续
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
接着他又返回了一个putVal方法
看一眼这个方法是啥,一看好家伙
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}不急咱一点一点拆着看
首先搞清楚前面定义的Node<K,V>[] tab这玩意是啥,有node节点
static class Node<K,V> implements Map.Entry<K,V>静态内部类再看一眼方法,是链表节点
先解释一下参数是什么意思
hash: 键的哈希值,用于确定键值对在数组中的位置。
key: 键,可以是任意类型的对象。
value: 值,可以是任意类型的对象。
onlyIfAbsent: 一个布尔值,表示是否只在键不存在时才插入值。
先看前面
首先判断数组是否为空或长度为零,如果是则调用resize方法。
resize方法是用来扩容的方法
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
然后根据哈希值和数组长度计算出键值对在数组中的索引i,并获取该位置的节点p。
如果p为空,则说明该位置没有发生哈希冲突,直接创建一个新节点并放入数组中。
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);那么剩下的情况就是该位置已经有元素了,发生了哈希冲突了,用else来嵌套剩下的情况
1.如果p的哈希值和键与传入的参数相同,则说明找到了相同的键,直接将p赋值给e。
e相当于一个中间变量
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;2.如果p的节点是treenode节点就把他放进去
看眼treenode是什么东西,发现是是一个静态内部类,并且里面有boolean red这个属性,是判断此节点是红还是黑的,原来这个东西是一个红黑树节点
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);3.如果都不是的话,就只有一种情况了,下面是个链表,要顺着往下遍历看看有没有相同元素
于是再用一个else来嵌套剩下的情况
3.1
使用一个循环遍历链表,每次将p的下一个节点赋值给e,并判断e是否为空或者与传入的参数相同。
TREEIFY_THRESHOLD这个玩意是类中的一个常量值为8
说明链表在长度为8时转换为红黑树
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {//如果e为空,则说明到达了链表尾部,没有找到相同的键
p.next = newNode(hash, key, value, null);//,创建一个新节点并插入到链表尾部,
if (binCount >= TREEIFY_THRESHOLD - 1) // 并判断是否需要将链表转化为红黑树。
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;//如果e不为空且与传入的参数相同,则说明找到了相同的键,跳出循环。
p = e;//每次循环后将e赋值给p,以便下一次循环使用
} 3.2
如果e不为空,则说明存在相同的键,需要更新其对应的值。
然后返回该节点的值不空
所以put返回的为旧节点的值非空,故add返回false显示添加失败
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}3.3
同理put返回的为旧节点的值为空,故add返回true显示添加成功
++modCount;//增加修改计数器modCount和元素个数size
if (++size > threshold)//判断是否需要扩容数组。
resize();
afterNodeInsertion(evict);//用afterNodeInsertion方法处理后续逻辑,并返回null。
return null;总结一下:
HashSet添加元素会调用HashMap的添加方法值作为key,一个空对象作为value
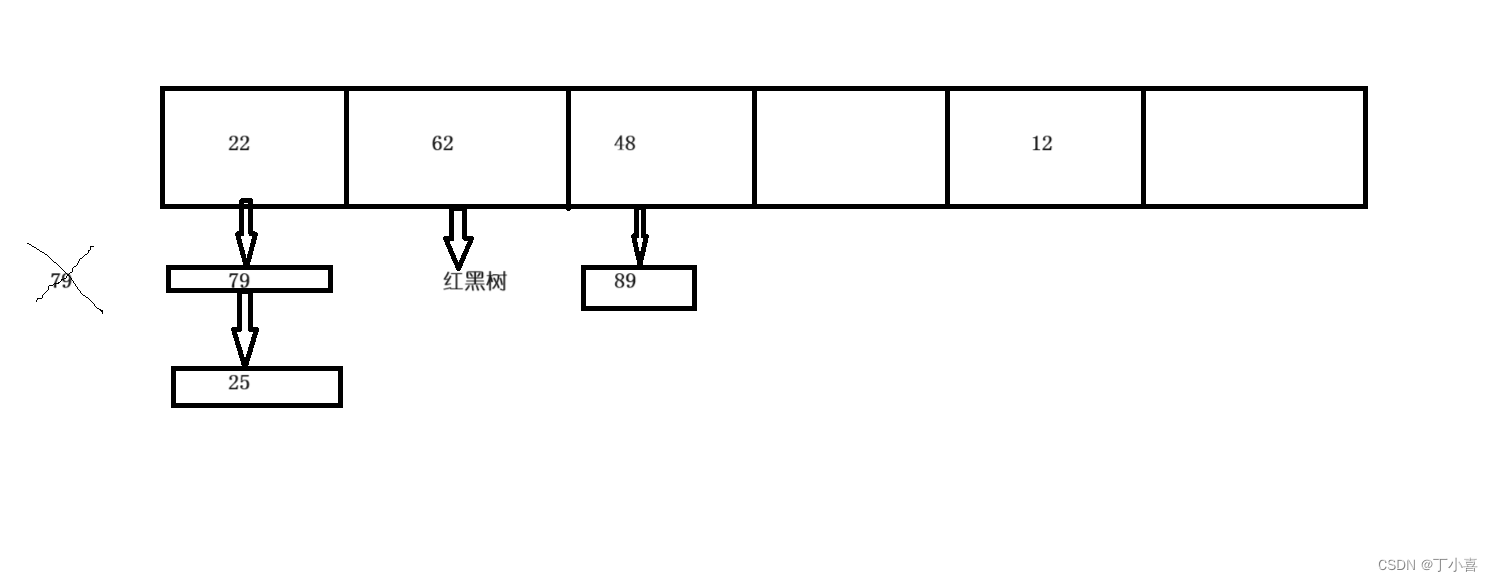
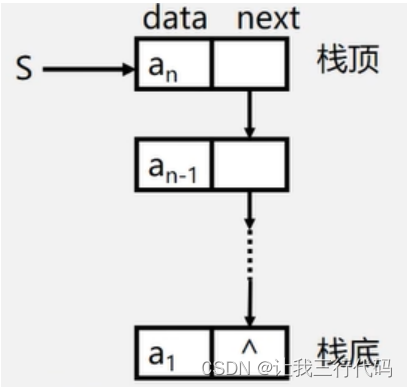
而HashMap用hash计算的出元素的hash值并放在对应的数组索引上,如果hash冲突了就在下面挂一个链表。如果找到了同一个元素就把新加入的元素值赋给旧元素。
当这条链表长度大于8时 ,这条链表自动转换成红黑树存储
大概长这个样子: