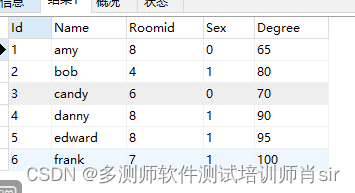
- 数学建模竞赛写作最重要的一点
- LaTeX 很重要 非常重要 非常重要
- 一定要规范 美观
写作注意事项
- 标准的附录
- 详实的支撑材料和清晰的支撑材料说明
- 文章中所有的图片都应该包含在支撑材料中
- 正确得引用参考文献
- 模型的评价部分应当包含
- 模型优点
- 模型缺点
- 改进方案
- 图像绘制应当标准
- 假设说明
- 简洁
- 只列出必要的假设而不是堆砌
- 应当包含合理性证明
不应当做的事情
- 不懂装懂
- 抄袭
微分方程的数值求解
IRK6解释
模型求解
我们选择使用截断误差更小的三级六阶隐式Runge-Kutta方法对模型进行试求解。
模型的刚性分析
刚性方程组对于数值解法的稳定性要求非常苛刻
方程组的刚性:
常微分方程初值问题的三级六阶隐式Runge-Kutta解法
递推公式:
初值条件:
模型求解结果
时间图:
相空间:
模型求解结果的稳定性检验
虽然在理论上,隐式方法多是无条件稳定的。但是,该方法的每一步递推都需要求解一非线性方程组。非线性方程组求解方法的选择将会显著影响模型求解的稳定性。我们选择使用scipy.optimize.solve 这一内置方法求解非线性方程组,其稳定域是未知的,因此仍然需要对模型求解结果进行稳定性检验。
我们采用调整求解步长的方法验证三级六阶隐式Runge-Kutta方法在该初值问题上的稳定性。
模型求解结果分析
求解结果分析
RK4解释
模型求解
我们选择使用截断误差为O(h^5)的四阶Runge-Kutta方法对模型进行试求解。
常微分方程初值问题的四阶龙格库塔解法:
递推公式:
初值条件:
模型求解结果
时间图:
相空间:
模型求解结果的稳定性检验
我们遗憾得指出,求解四阶Runge-Kutta在该初值问题上的稳定域的过程较为复杂,我们采用调整求解步长的方法验证四阶Runge-Kutta方法在该初值问题上的稳定性。
时间图:
相空间:
误差图:
模型试求解结果分析
求解结果分析
优化模型的求解
随机数问题
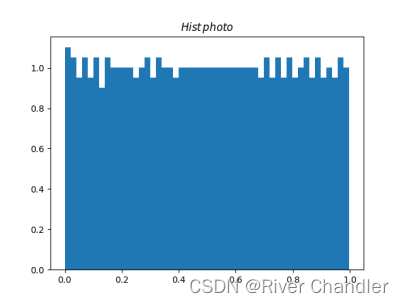
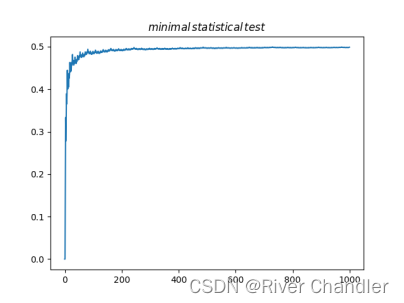
我们提到,遗传算法与模拟退火算法的优异表现依赖于随机数生成器的表现。我们使用的一直是Python内置的random 模块。其均匀性与收敛速度可能并不足够理想,可以使用Sobol序列或者Halton序列制作性质更加良好的随机数生成器,我们将相关的随机数生成器放在附录中供参考。图为Halton生成器的Hist检验与minimal statistical检验。
- 这是我写的一个随机数生成器,尽管参考,因为没有啥高难度的东西,都最简单的
import matplotlib.pyplot as plt
import time
import copy
import math
class randomgenerator():
def __init__(self,seed=0):
self.state = seed
def help_doc(self):
print("not finished!")
#Linear Congruential Generator
#linear congruential generator
def LGC(self,a=1103515245,c=12345,m=2**31):
#best self,a=1103515245,c=12345,m=2**31
self.state = (a * self.state + c) % m
return self.state / m
def LGCrand(self,a=1103515245,c=12345,m=2**31,Len=1000,Dim=1):
state = self.state
R = [[0 for j in range(Dim)] for i in range(Len)]
for j in range(Len):
for i in range(Dim):
state = (a * state + c) % m
R[j][i] = state / m
return R
#lagged fibonnaci generators
def LFG(self,seed=[time.time(),time.time()+1,time.time()+2]):
lag1 = seed[0]
lag2 = seed[1]
current_seed = copy.deepcopy(seed)
current_seed = [current_seed[j] for j in range(1,len(seed))]+[sum(current_seed)%1]
#return [current_seed[-1],["seed1:",seed[0],"seed2:",seed[1]]]
return current_seed[-1]
def LFGrand(self,seed=[time.time(),time.time()+1,time.time()+2],Len=10,Dim=2):
R = [[0 for j in range(Dim)] for i in range(Len)]
lag1 = seed[0]
lag2 = seed[1]
current_seed = copy.deepcopy(seed)
def fun_in_LFGrand():
nonlocal lag1
nonlocal lag2
nonlocal current_seed
current_seed = [current_seed[j] for j in range(1,len(seed))]+[sum(current_seed)%1]
lag1 = lag2
lag2 = current_seed[-1]
return lag2
for j in range(Len):
for i in range(Dim):
R[j][i] = fun_in_LFGrand()
return R
#multiple recursive generators
def MRG(self,seed=1000,r1=123456789,r2=987654321,a=428773,m=2**32):
#f = lambda y1,y2:(a*r1+r2)%m
M = []
for i in range(seed):
r1,r2 = (a*r1+r2)%m,r1
M.append((a*r1+r2)%m/m)
return M
#Inverse-Transform Method
def ITM(self,Len=1000):
#print("Warning!using sin(x)^2 [0,pi/2]as cdf")
cdf = lambda x:math.sin(x)**2
pdf = lambda x:math.sin(x)*math.cos(x)*2
n_samples=1000
def Inverse_Transform(Y):
nonlocal n_samples
nonlocal cdf
x = [i*math.pi/2/n_samples for i in range(n_samples)]
y = [cdf(i) for i in x]
ABS = [abs(Y-i) for i in y]
return x[ABS.index(min(ABS))]
M = []
for i in range(Len):
M.append(Inverse_Transform(self.LGC()) )
return M
#Accept-Reject method
def ARM(self):
f = lambda x:1
M = math.sqrt(2*math.exp(1)/math.pi)
while True:
x = self.LGC()
y = self.LGC()
if y <= f(x)/M:
return x
#halton
def halton(self,Len=1000,base=3):
def halton_f():
nonlocal Len
nonlocal base
n,d = 0,1
for L in range(2*Len):
x = d-n
if x == 1:
n = 1
d *= base
else:
y = d//base
while x <= y:
y//=base
n = (base+1)*y-x
yield n/d
f = halton_f()
return [next(f) for i in f]
def chi_square_test(self,observed_values):
from scipy.stats import chisquare
import numpy as np
expected_values = \
np.ones(shape=len(observed_values)) * (sum(observed_values) / len(observed_values))
chi_squared_statistic,p_value = \
chisquare(observed_values, expected_values)
return chi_squared_statistic, p_value
def minimal_statistical_test(self,List):
num = len(List)
ave = [0 for i in range(num)]
for i in range(1,num):
ave[i] = sum(List[:i])/i
plt.plot(range(num),ave)
plt.title("$minimal\,statistical\,test$")
plt.pause(0.01)
def Hist(self,List,Bins=50,Density=True):
plt.title("$Hist\,photo$")
plt.hist(List,bins=Bins,density=Density)
plt.pause(0.01)
####testing####
if __name__ == "__main__":
r = randomgenerator()
s = r.MRG
M = s()
r.Hist(M)
r.minimal_statistical_test(M)
c,p = r.chi_square_test(M)
print("c=",c)
print("p=",p)
遗传算法解释
遗传算法虽然会在随机性上消耗和浪费大量的算力与时间,但其在全局搜索与小空间搜索上往往有突出表现。我们最终选择增强精英保留遗传算法求解这个优化问题,程序实现基于Python geatpy模块。
遗传算法通过模拟生物界自然选择过程以实现最优化问题的求解。依据适应度函数(目标函数)的大小确定自然界中的个体(当前解)竞争力。每个个体(当前解)都将以一串二进制数表示。竞争力高的个体将获得更多的生存机会,这一点通常在新生代的占比中体现出来。
在自然界中,当老一代走向新一代时,必然会发生基因重组,这会加大物种的多样性。与之对应的,在遗传算法的迭代过程中,个体交换其对应的部分二进制码,以求找到全局最优解。为增大找到全局最优解的可能,遗传算法会在迭代中考虑变异(对当前解做随机扰动)等情况。
...
与常用的遗传算法不同,在群体代际更迭时,增强精英保留遗传算法会更多得保留最优个体而避免群体中的优秀部分在更迭时中丢失。
我们设置的最大进化代数为:
我们设置的优化停滞退出阈值为:
遗传算法求解结果:
模拟退火解释
为了克服优化算法法初值依赖性和检验遗传算法的求解结果,我们以遗传算法的求解结果为算法初始点,进行数次模拟退火过程。
模拟退火算法稳定得控制控制参数(金属温度)降低,通过对当前解的随机扰动获得新解,依据Metropolis准则判断是否接受新解,使目标函数(金属内能)降低,直至趋于最小值。
我们设定的控制参数初始值(金属初始温度)为:
我们设定的迭代退出标准为:
这是模拟退火算法的求解结果
我们可以看到模型求解是较为准确的




![Vue.js入门模板语法[上] 及Vue.js实现购物车---详细讲解](https://img-blog.csdnimg.cn/45dcc351292a4384b63c02af366b71c9.gif)