1 图的基本概念

 

图(Graph) 是由一个顶点集V和一个弧集E构成的网状数据结构，记作 $G=(V,E)$ 在图中，数据元素通常称作顶点(Vertex)，V是顶点的有穷非空集合；V R VRVR是两个顶点之间的关系的集合

线性表可以为空表,树可以是空数,但是图不可以为空,即图一定是非空集

---

 

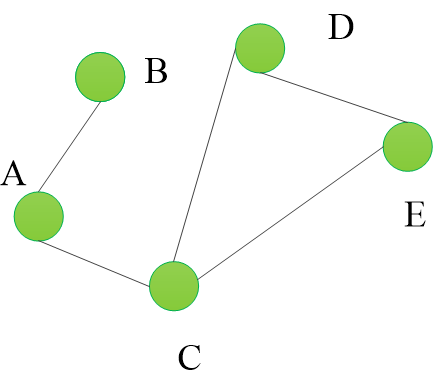
2 无向图和有向图

 

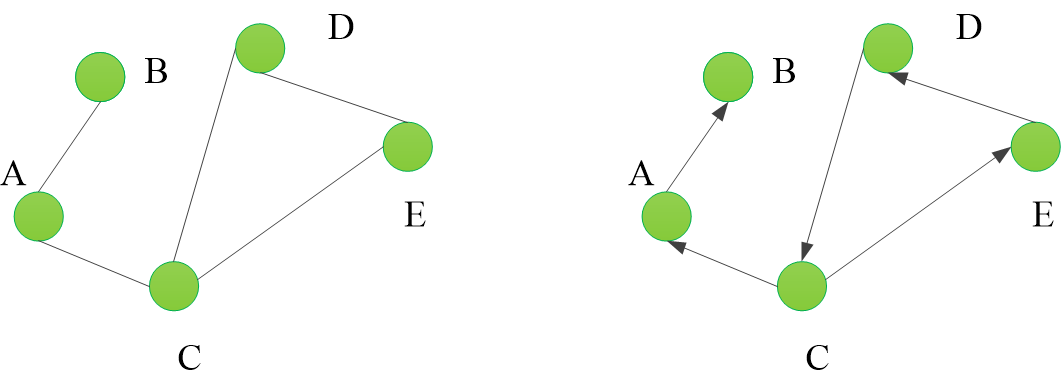
在一个图中，如果任意两个顶点构成的偶对(a,b)属于E是无序的,即顶点之间的连线是没有方向的,则称该图为无向图。

在一个图中，如果任意两个顶点构成的偶对(a,b)属于E是有序的,即顶点之间的连线是有方向的,则称为有向图

---

 

3 图相关的关键术语

 

顶点 :  图中的节点

弧 :   有向图 v为起点 w为终点 <v,w>表示v到w的一条弧

边 :    无向图 有<v,w>就有<w,v>

权 :   可以理解成边的长度

顶点的度 :    和该顶点相关联的边的数目 度 = 入度 + 出度

顶点的入度 :   该顶点为终点

顶点的出度 :   改顶点为起点

路径 :    从一个顶点到另一个顶点的路径

连通图 :    任意两个顶点都是连通的

---

 

4 图的相关性质

 
设 n为图中的节点数
e为边或弧的数目 则有如下性质

1. 在无向图中
   e的取值范围是 0 ~ n(n-1)/2
   在无向图中,如果有e = n(n-1)/2则,则为完全图
2. 在有向图中
   e的取值范围是 n(n-1)
   在有向图中，如有n(n-1)条弧，则称为有向完全图

---

 

5 图的存储

 

邻接表法 邻接矩阵法

图

4.1 邻接表法

 
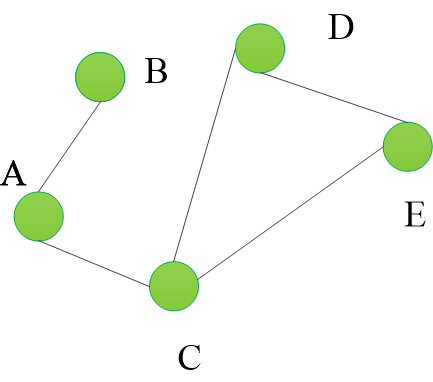
使用链表来表示图的连接关系,对于每个顶点,使用链表存储与其相邻的顶点,邻接表的优点是对于稀疏图而言,存储空间较小;同时可以快速遍历每一个顶点的邻接顶点,但是查找两个顶点之间是否存在边的时间复杂度为 $O(k)$,其中k是相邻顶点的数量

特点 :

1. 在邻接表中，给定一顶点就很容易地找到它所有邻边

2. 在有向图的邻接表中，求一个给定顶点的出度只需计算其邻接表中的结点个数即可，但求某顶点的入度，则需要遍历全部的邻接表

3. 图的邻接表表示并不唯一，因为各边表结点的顺序是任意的

4. 邻接表便于增加和删除节点，便于统计边数

邻接表属于链式存储，但邻接表的表头属于顺序存储结构

4.2 邻接矩阵法

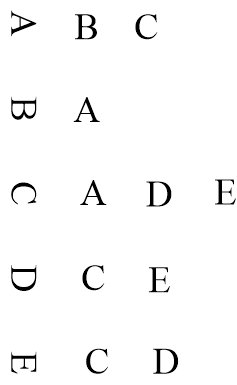
使用一个二维数组来表示图的连接关系,对于n个顶点的无向图,使用 n * n的矩阵表示 如果两个顶点 i和j之间存在边,则在矩阵中 (i,j) 和 (j,i)的值为1,否则为0,(i,j) 位置的值表示从顶点i到顶点j的边

邻接矩阵的优势是查找两个顶点之间是否存在边的时间复杂度为 $O(n)$

无向图的邻接矩阵一定是对称矩阵

---

 

6 图的代码表示

 
顶点

public class Node {
    // 点上的值
    public int value;
    // 一个点的入度 有多少条边指向自己
    public int in;
    // 一个点的出度 一个点指向其它点的边个数
    public int out;

    // 点发散出去边连接的点
    public ArrayList<Node> nexts;
    // 属于这个节点的边有哪些
    public ArrayList<Edge> edges;

    public Node(int value){
        this.value = value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

边

public class Edge {
    public int weight;// 权值可以表示距离
    public Node from;// 
    public Node to;// 

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

图

/**
 * 图的表示方式 邻接图 邻接矩阵
 * @author Mrchao
 * @version 1.0.0
 * @date 2023-07-10
 */
public class Graph {
    // 点集 key 点的编号 Node实际的点
    public HashMap<Integer,Node> nodes;
    // 边集
    public HashSet<Edge> edges;

    public Graph(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}