前言

本篇文章博主将会与大家一起学习二叉树的构建与一些基本操作实现，那么对于二叉树来说：递归是不可绕开的话题，在本篇文章中你会看到很多的递归，递归的核心思想就是分割子问题，他异于我们之前学习的遍历枚举等思想，所以希望你能有所收获🌍

欢迎大家📂收藏📂以便未来做题时可以快速找到思路，巧妙的方法可以事半功倍。

=========================================================================

GITEE相关代码：🌟fanfei_c的仓库🌟

=========================================================================

1.前序建立二叉树

首先我们输入一段前序序列，用字符串存储，空节点的部分我们用字符'#' 替代，利用*pi作为下标，遍历该字符串。

前序：将字符赋给当前节点的数据域，*pi的值+1，给当前节点的左孩子执行相同操作，给当前节点的右孩子执行相同操作，采用递归方式完成。

那么你可以写出中序建立二叉树的算法么？

代码实现：

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	root->_data = a[(*pi)++];

	root->_left = BinaryTreeCreate(a, pi);
	root->_right= BinaryTreeCreate(a, pi);
	return root;
}

为什么使用指针pi，而不用整型pi？

若传整型，在函数递归的过程中，由于函数栈帧的关系，整型pi的值不会保留，所以需要传递指针。

2.销毁二叉树

销毁二叉树比较简单。

注意：销毁二叉树采用的是后序遍历的方式，因为如果先销毁根节点，那么就找不到孩子节点了。

代码实现：

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root)
	{
		BinaryTreeDestory(&(*root)->_left);
		BinaryTreeDestory(&(*root)->_right);
		free(*root);
        *root = NULL;
	}
}

3.统计

我们主要看一下统计第k层节点的算法：

如何判断何时递归到第k层呢？

想要到达第k层，我们可以利用递归每次让k-1，当k的值为1的时候，那么此时我们就来到了第k层
可以来到第k层的，也就是k==1时我们返回1
递归还是采用双路递归，即返回左右子树的和即可

代码实现：

//计算节点数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

//计算叶子节点数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->_left == NULL && root->_right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->_left) 
        + BinaryTreeLeafSize(root->_right);
}

// 二叉树第k层节点个数（假设从第1层开始）
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BinaryTreeLevelKSize(root->_left, k-1) 
        + BinaryTreeLevelKSize(root->_right, k-1);
    //递归每次让k-1，当k的值为1的时候，那么此时我们就来到了第k层
}

//二叉树深度
int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return fmax(BinaryTreeHeight(root->_left)
        , BinaryTreeHeight(root->_right))+1;
}

4.查找值为x的节点

该递归过程可以理解为前序思想，即如果根节点的值为x，那么肯定就可以直接返回，如果不同，我们就可以向左子树和右子树方向考虑，具体的设计可见代码。

代码实现：

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->_data == x)
	{
		return root;
	}
	BTNode* ret = NULL;
	ret = BinaryTreeFind(root->_left,x);
	if (ret)
	{
		return ret;
	}
	ret = BinaryTreeFind(root->_right, x);
	if (ret)
	{
		return ret;
	}
	return NULL;
}

5.前中后序遍历

代码实现：

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%c ", root->_data);
	BinaryTreeInOrder(root->_left);
	BinaryTreeInOrder(root->_right);
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeInOrder(root->_left);
	printf("%c ", root->_data);
	BinaryTreeInOrder(root->_right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BinaryTreeInOrder(root->_left);
	BinaryTreeInOrder(root->_right);
	printf("%c ", root->_data);
}

6.层序遍历

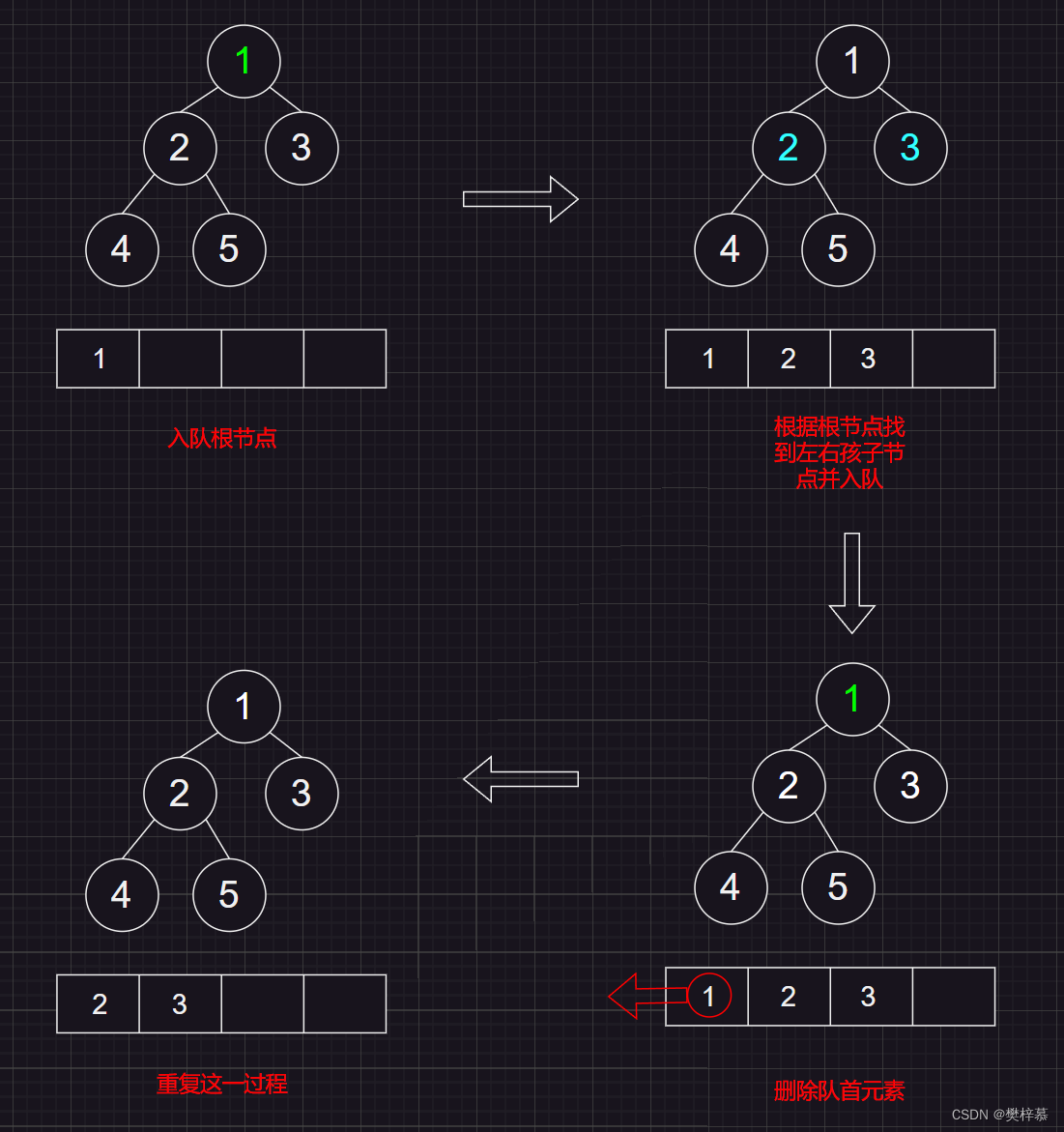
层序遍历的实现需要用到队列的逻辑结构。

首先将根节点入队，输出队首元素，并根据根节点找到左右孩子节点并入队，然后出队根节点，此时队首元素更新为根节点的左子树，再以此左子树为根循环这个过程，就能成功实现层序遍历。

代码实现：

void BinaryTreeLevelOrder(BTNode* root)
{
	Que q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%c ", front->_data);
		if (front->_left)
		{
			QueuePush(&q, front->_left);
		}
		if (front->_right)
		{
			QueuePush(&q, front->_right);
		}
		QueuePop(&q);
	}
	QueueDestroy(&q);
	return;
}

7.判断二叉树是否为完全二叉树

完全二叉树通俗的讲就是每个节点都是连续的，不存在某个节点之前存在空节点的情况，那么根据这个特性，我们同样可以利用层序遍历的思想，利用队列的逻辑结构来解决。

思路：与层序遍历不同的是，我们不管左右子树是否为空都入队，这样在循环结束时，队列中要么全为空，此时证明该二叉树是完全二叉树，如果队列中但凡存在一个不为空的情况，那就证明该二叉树不为完全二叉树。

代码实现：

bool BinaryTreeComplete(BTNode* root)
{
	Que q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);
		QueuePop(&q);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}