【C++】map与set的封装

news2024/11/26 15:28:18

文章目录

  • 前言
  • 正文
    • 1. 类型的泛化
    • 2.仿函数
    • 3.迭代器
      • 3.1正向迭代器
        • 3.1.1 ++
        • 3.1.2 - -
        • 3.1.3 *
        • 3.1.4 ->
        • 3.1.5 !=
        • 完整版代码
    • 4.[]（map）
  • 框架
    • 1.红黑树
    • 2.set
    • 3.map
  • 总结

前言

 在学习了红黑树之后，我们便可以尝试初步的在红黑树的基础上封装出map与set，好了，话不多说，进入今天的学习吧！

所需知识：

  1. 模板,主要为typename的特殊用法，模板参数，类模板。
  2. 迭代器与const迭代器
  3. 仿函数、反向迭代器
  4. 红黑树

正文

1. 类型的泛化

 我们先分析map与set以及红黑树的模板参数。

  1. map 存的是key——val，键值对。
  2. set 存的是key。
  3. 红黑树存的是 key——val。

 因此，为了适配set，红黑树里面存的是key，为了适配map红黑树存的是key——val, 如何实现呢？

那不如，设红黑树的存放的val是T类型，可以是key，也可以是key——val。

  • 既然这样，我们就将原先的结点改为T类型的。
template<class T>
struct RBTreeNode
{

	typedef RBTreeNode<T> Node;
	RBTreeNode(const T& data)
		:_data(data)
		,_right(nullptr)
		,_left(nullptr)
		,_parent(nullptr)
		,_col(RED)
	{}

	Node* _right;
	Node* _left;
	Node* _parent;
	T _data;
	Color _col;
};

那既然这样，又会引出两个问题：

  1. 模板参数的Key还有用吗？
  2. 插入的数据类型也要变为T，如何进行比较？

先来解决第一个问题，Key有用吗？首先要明白Key是一个类型，在定义变量或者作为函数参数时要使用，很显然红黑树的查找的函数的参数类型是Key，因此有用，且不能舍弃。

2.仿函数

 接着解决第二个问题，插入时既然T可以是key，也可以是pair<key,val> ,我们在找结点的位置的过程中，是通过key值进行查找的,因此又面临两种情况：

  1. T是key时，结点中存的是key可以直接进行比较。
  2. T是pair<key,val>,结点中存的是pair<key,val>直接比较，是无法得出正确结果的，我们看库里的实现即可清楚。
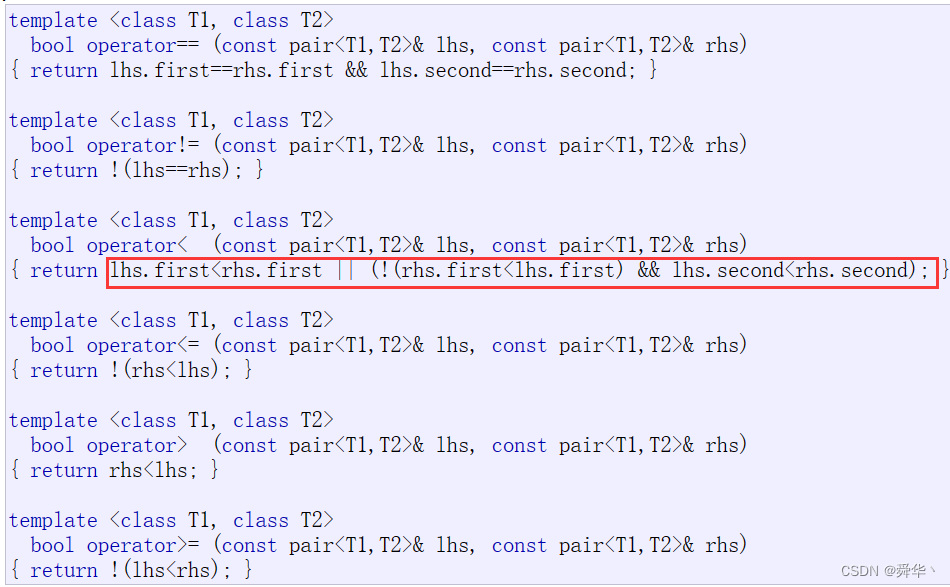
    在这里插入图片描述
    库里的实现涉及到第二参数，因此无法准确的得出正确结果，因此需要我们自己写一个仿函数，那因为map需要写，set也要适配红黑树，因此也需要写一个仿函数，返回key即可。

set实现：

template<class K>
struct SetOfT
{
	K operator()(const K& val)
	{
		return val;
	}
};

map实现:

template<class K, class V>
struct MapOfT
{
	const K operator()(const  pair<const K, V>& val)
	{
		return val.first;
	}
};

3.迭代器

3.1正向迭代器

 根据之前的内容的学习，我们是封装出来一个通用的正向迭代器，通过模板参数控制其为const还是非const迭代器。

基本框架：

	template<class T,class Ref,class Ptr>
	struct __TreeIterator
	{
		
		typedef __TreeIterator<T, T&, T*> iterator;
		typedef RBTreeNode<T> Node;
		typedef __TreeIterator<T,Ref,Ptr> self;

		__TreeIterator(Node* val)
			:_node(val)
		{}
		//此构造用于将非const迭代器转换为const迭代器，从而实现类型转换的功能。
		__TreeIterator(const iterator& val)
			:_node(val._node)
		{}
		//前置++
		self& operator++();
		//后置++
		self operator++(int);
		//后置--
		self operator--(int);
		//解引用
		Ref operator*();
		//箭头
		Ptr operator->();
		//不等于
		bool operator!=(const __TreeIterator& it);

		Node* _node;
	};

3.1.1 ++

由于三叉链的结构，父节点是很容易找到的，因此可以直接用循环写一个。

原理： 中序遍历

  1. 开始节点树的最小节点。
  2. 根据中序遍历的过程遍历整棵树。

图解：
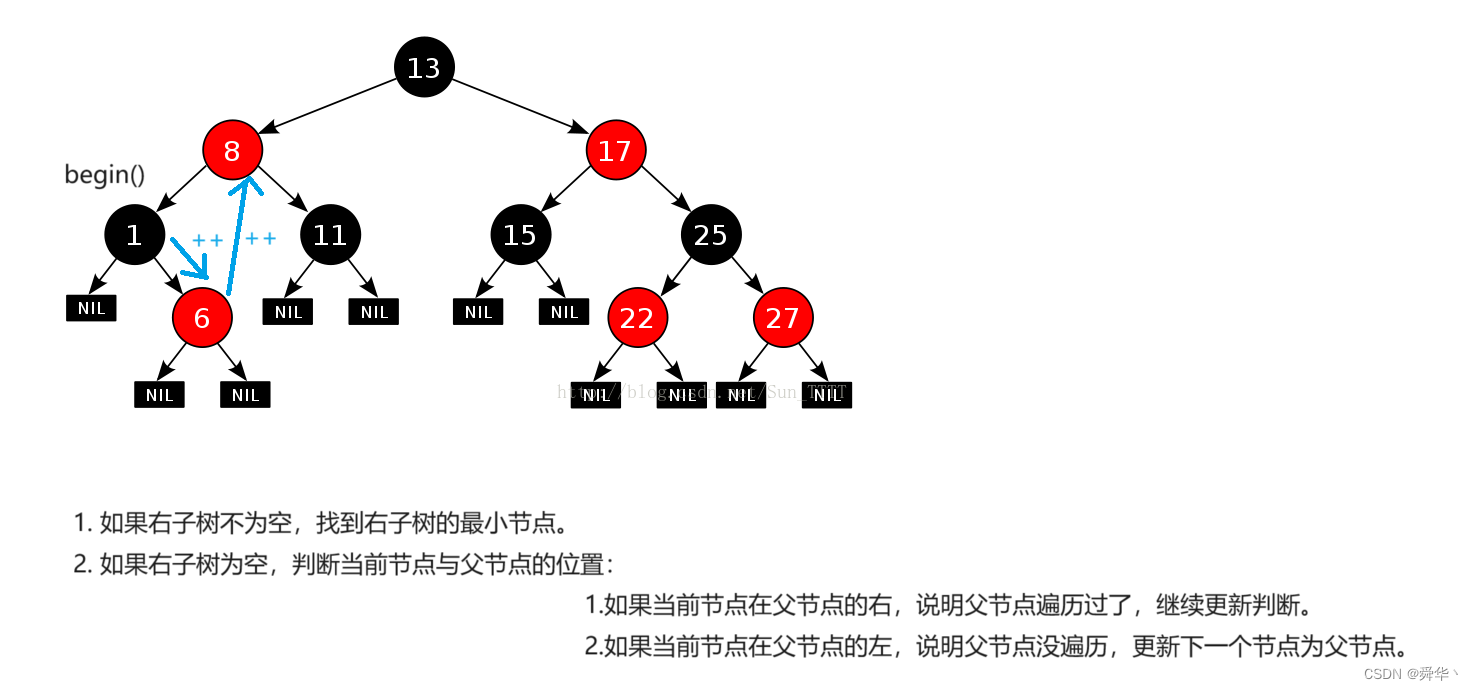
在这里插入图片描述

		self& operator++()
		{
			Node* cur = _node;
			assert(cur);
			if (cur->_right)
			{
				//如果右子树不为空，访问其右子树的最左结点。
				Node* MostLeft = cur->_right;
				while (MostLeft && MostLeft->_left)
				{
					MostLeft = MostLeft->_left;
				}
				_node = MostLeft;
			}
			else
			{
				//右子树为空，访问其祖先

				Node* parent = cur->_parent;

				//结点为其父节点的左边，访问父节点即可
				if (parent && parent->_left == cur)
				{
					_node = parent;
				}
				//结点为其父节点的右边，访问父亲的父亲
				else
				{
					while (parent && parent->_right == cur)
					{
						cur = parent;
						parent = parent->_parent;
					}
					_node = parent;
				}
			}
			return *this;
		}

3.1.2 - -

  • 与 ++同思路。

图解：
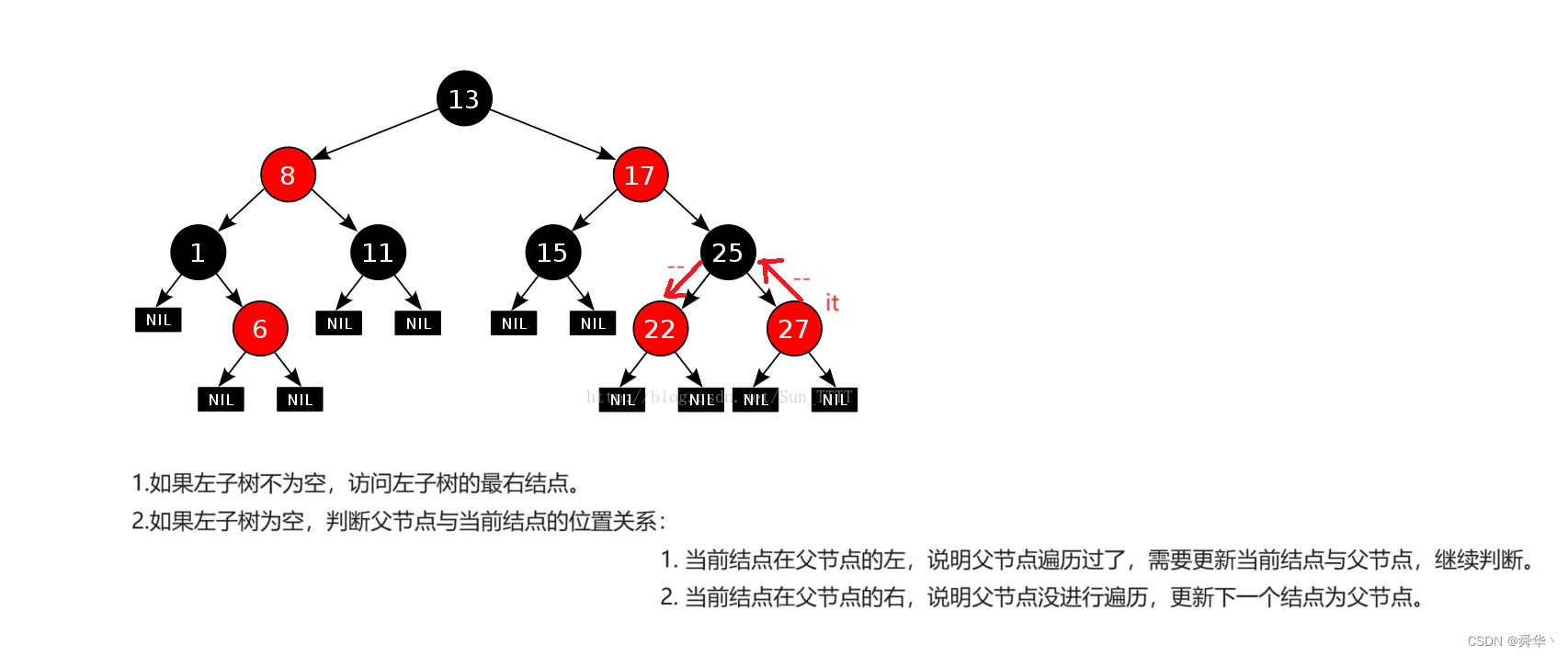
在这里插入图片描述
注意：当为空时，–我在这实现的是不可以的，但是库里面的是可以的，因为库里的结构是这样的。

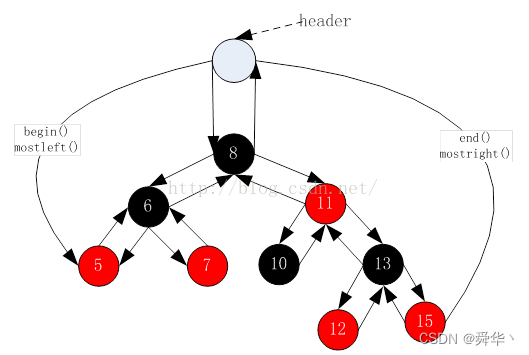
在这里插入图片描述
库里的判断条件是这样的：当node为header时，node就转换其右边结点，也就是右树的最大结点。
在这里插入图片描述
说明一下：这样实现可能会导致增加了维护最大和最小节点的成本，每次插入和删除都得判断一下，不过也还好。

因此：这里我们只是实现正向的迭代器，反向的迭代器我们没有写，如果不采用库里的结构，我们也可以用友元+指针+前置类型声明的方式进行实现。

self& operator--()
{
	Node* cur = _node;
	if (cur->_left)
	{
		//访问最右结点
		Node* most_right = cur->_left;
		while (most_right && most_right->_right)
		{
			most_right = most_right->_right;
		}
		_node = most_right;
	}
	else
	{
		Node* parent = cur->_parent;
		if (parent->_right == cur)
		{
			//父节点右为cur，该访问父节点了。
			_node = parent;
		}
		else
		{
			//找到父亲作为cur的结点。
			while (parent && parent->_left == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
	}

	return *this;
}

3.1.3 *

Ref operator*()
{
	return _node->_data;
}

3.1.4 ->

Ptr operator->()
{
	return &(_node->_data);
}

3.1.5 !=

bool operator!=(const __TreeIterator& it)
{
	return _node != it._node;
}

完整版代码

	template<class T,class Ref,class Ptr>
	struct __TreeIterator
	{

		typedef __TreeIterator<T, T&, T*> iterator;
		typedef RBTreeNode<T> Node;
		typedef __TreeIterator<T,Ref,Ptr> self;

		__TreeIterator(Node* val)
			:_node(val)
		{}
		__TreeIterator(const iterator& val)
			:_node(val._node)
		{}

		//前置++
		self& operator++()
		{
			Node* cur = _node;
			assert(cur);
			if (cur->_right)
			{
				//如果右子树不为空，访问其右子树的最左结点。
				Node* MostLeft = cur->_right;
				while (MostLeft && MostLeft->_left)
				{
					MostLeft = MostLeft->_left;
				}
				_node = MostLeft;
			}
			else
			{
				//右子树为空，访问其祖先

				Node* parent = cur->_parent;

				//结点为其父节点的左边，访问父节点即可
				if (parent && parent->_left == cur)
				{
					_node = parent;
				}
				//结点为其父节点的右边，访问父亲的父亲
				else
				{
					while (parent && parent->_right == cur)
					{
						cur = parent;
						parent = parent->_parent;
					}
					_node = parent;
				}
			}
			return *this;
		}

		self operator++(int)
		{
			 self tmp(_node);
			 ++(*this);
			 return tmp;
		}
		self& operator--()
		{
			Node* cur = _node;
			if (cur->_left)
			{
				//访问最右结点
				Node* most_right = cur->_left;
				while (most_right && most_right->_right)
				{
					most_right = most_right->_right;
				}
				_node = most_right;
			}
			else
			{
				Node* parent = cur->_parent;
				if (parent->_right == cur)
				{
					//父节点右为cur，该访问父节点了。
					_node = parent;
				}
				else
				{
					//找到父亲作为cur的结点。
					while (parent && parent->_left == cur)
					{
						cur = parent;
						parent = parent->_parent;
					}
					_node = parent;
				}
			}

			return *this;
		}
		self operator--(int)
		{
			self tmp(_node);
			(*this)++;
			return tmp;
		}
		Ref operator*()
		{
			return _node->_data;
		}
		Ptr operator->()
		{
			return &(_node->_data);
		}
		bool operator!=(const __TreeIterator& it)
		{
			return _node != it._node;
		}
		Node* _node;
	};

4.[]（map）

我们要实现的insert接口为：
在这里插入图片描述

因此我们实现的红黑树的接口为：

pair<iterator,bool> insert(const T& val)
{
	//第一步：插入操作
	//如果根节点为空
	if (_root == nullptr)
	{
		_root = new Node(val);
		_root->_col = BLACK;
		return make_pair(iterator(_root), true);
	}
	else
	{
		KeyOfT sel;//select里面的key
		Node* cur = _root, *parent = _root;
		while (cur)
		{
			if (sel(cur->_data) > sel(val))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (sel(cur->_data) < sel(val))
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return make_pair(iterator(cur), false);
			}
		}
		cur = new Node(val);
		if (sel(parent->_data) > sel(val))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		//变色逻辑略，重点在框架。
		return make_pair(iterator(newnode), true);
	}
}

map接口的实现为：

pair<iterator,bool> insert(const pair<K,V>& data)
{
	return _tree.insert(data);
}
mapped_type& operator[](const key_type& data)
{
	pair<iterator, bool> x = _tree.insert(val_type(data,mapped_type()));
	return x.first->second;
}

set的接口为：

pair<iterator,bool> insert(const K& data)
{
	pair<typename rb_type::iterator, bool> k = _tree.insert(data);
	return pair<iterator,bool>(k.first,k.second);
}

补充小知识：迭代器转const迭代器

先强调：

  1. const迭代器与非const迭代器是两种完全不同的自定义类型。
  2. 内置类型默认支持隐式类型转换，自定义类型需要有合适的构造函数才可实现隐式类型的转换，且explict可阻止隐式类型转换的发生。

因此：我们需要在模板内部写一个合适的构造函数，且其成员是公有的，才可实现自定义类型的转换。

框架

1.红黑树

运用封装知识的框架：

	template<class Key,class T,class KeyOfT>
	class RBTree
	{
	public:
		typedef RBTreeNode<T> Node;
		typedef __TreeIterator<T,T&,T*> iterator;
		typedef __TreeIterator<T, const T&, const T*> const_iterator;
		const_iterator begin()const
		{
			Node* mostleft = _root;
			while (mostleft && mostleft->_left)
			{
				mostleft = mostleft->_left;
			}
			return mostleft;
		}
		iterator begin()
		{
			Node* mostleft = _root;
			while (mostleft && mostleft->_left)
			{
				mostleft = mostleft->_left;
			}
			return mostleft;
		}
		const_iterator end()const
		{
			return nullptr;
		}
		iterator end()
		{
			return nullptr;
		}
		Node* find(const Key& key)
		{
			KeyOfT sel;
			Node* cur = _root;
			while (cur)
			{
				if (sel(cur->_data) > key)
				{
					cur = cur->_right;
				}
				else if (sel(cur->_data) < key)
				{
					cur = cur->_left;
				}
				else
				{
					return cur;
				}
			}
			return nullptr;
		}
		pair<iterator,bool> insert(const T& val)
		{
			//第一步：插入操作
			//如果根节点为空
			if (_root == nullptr)
			{
				_root = new Node(val);
				_root->_col = BLACK;
				return make_pair(iterator(_root), true);
			}
			else
			{
				KeyOfT sel;
				Node* cur = _root, * parent = _root;
				while (cur)
				{
					if (sel(cur->_data) > sel(val))
					{
						parent = cur;
						cur = cur->_left;

					}
					else if (sel(cur->_data) < sel(val))
					{
						parent = cur;
						cur = cur->_right;

					}
					else
					{
						return make_pair(iterator(cur), false);
					}
				}
				cur = new Node(val);
				if (sel(parent->_data) > sel(val))
				{
					parent->_left = cur;
				}
				else
				{
					parent->_right = cur;
				}

				//根节点可能为红色,不管红色还是黑色都弄成黑色
				_root->_col = BLACK;
				return make_pair(iterator(newnode), true);
			}
		}
	private:

		Node* _root = nullptr;
	};
};

2.set

	template<class K>
	class set
	{
		template<class K>
		struct SetOfT
		{
			K operator()(const K& val)
			{
				return val;
			}
		};
		//typedef
		//类型
		typedef K key_type;
		typedef K val_type;
		typedef SetOfT<K> set_of_key;
		typedef RBTree<key_type, val_type, set_of_key> rb_type;
		typedef K key_type;
		typedef K val_type;
		typedef SetOfT<K> set_of_key;
		typedef RBTree<key_type, val_type, set_of_key> rb_type;
		//typename的作用：声明其为类型。
		typedef typename rb_type::Node Node;
	public:
		//迭代器
		typedef typename rb_type::const_iterator const_iterator;
		//不管是普通还是const迭代器set的key值都不可被修改。
		typedef const_iterator iterator;
		const_iterator begin() const
		{
			return _tree.begin();
		}
		const_iterator end() const
		{
			return _tree.end();
		}
	public:
		Node* find(const K& key)
		{
			return _tree.find(key);
		}
		pair<iterator,bool> insert(const K& data)
		{
			pair<typename rb_type::iterator, bool> k = _tree.insert(data);
			//这里涉及到普通迭代器转换成const迭代器。
			return pair<iterator,bool>(k.first,k.second);
		}
	private:
		rb_type _tree;
	};

3.map

template<class K,class V>
class map
{
	//类型
	typedef K key_type;
	typedef pair<const K, V> val_type;
	template<class K, class V>
	struct MapOfT
	{
		const K operator()(const  pair<const K, V>& val)
		{
			return val.first;
		}
	};
	typedef MapOfT<K, V> map_of_key;
	typedef RBTree<key_type, val_type, map_of_key> rb_type;
public:
	
	typedef typename rb_type::Node Node;
	//迭代器
	typedef typename rb_type::iterator iterator;
	typedef typename rb_type::const_iterator const_iterator;
	typedef V mapped_type;
	iterator begin()
	{
		return _tree.begin();
	}
	const_iterator begin()const
	{
		return _tree.begin();
	}
	iterator end()
	{
		return _tree.end();
	}
	const_iterator end()const
	{
		return _tree.end();
	}
	bool find(const K& key)
	{
		return _tree.find(key);
	}
	pair<iterator,bool> insert(const pair<K,V>& data)
	{
		return _tree.insert(data);
	}
	mapped_type& operator[](const key_type& data)
	{
		pair<iterator, bool> x = _tree.insert(val_type(data,mapped_type()));
		return x.first->second;
	}

private:

	rb_type _tree;
};

总结

 模板，迭代器，仿函数，分开起来，或许不难，但是合起来，还是有点难度的，毕竟封装也是套娃，也挺麻烦的，尤其是模板的一大缺陷，增加了编译器识别问题的难度。

 如果有所帮助，不妨点个赞鼓励一下吧！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1023649.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python日志处理器，同时打印到控制台和保存到文件中，并保证格式一致

Python日志处理器，同时打印到控制台和保存到文件中，并保证格式一致

使用logging模块的时候&#xff0c;默认是输出到控制台的&#xff0c;当然也可以配置输出到文件中&#xff0c;但是当你配置了文件后&#xff0c;控制台的输出就消失了&#xff0c;所以&#xff0c;需要一个策略即能保存到文件中&#xff0c;又能输出到控制台中。 下面是我做的…
阅读更多...
ORB-SLAM2实时稠密地图，解决运行报段错误（核心已转储）运行数据集时出现段错误，出现可视化界面后闪退（添加实时彩色点云地图+保存点云地图）

ORB-SLAM2实时稠密地图，解决运行报段错误（核心已转储）运行数据集时出现段错误，出现可视化界面后闪退（添加实时彩色点云地图+保存点云地图）

高翔的稠密建图仓库 1. git clone https://github.com/gaoxiang12/ORBSLAM2_with_pointcloud_map.git 2. 去ORB SLAM2里拷贝Vocabulary到/home/cgm/ORBSLAM2_with_pointcloud_map/ORB_SLAM2_modified文件夹下 3. 删除一些build文件夹 删除ORB_SLAM2_modified/Thirdparty/DB…
阅读更多...
国产手机芯片4G方案_紫光展锐安卓核心板虎贲4G智能模块方案定制

国产手机芯片4G方案_紫光展锐安卓核心板虎贲4G智能模块方案定制

元器件清单即BOM物料清单&#xff0c;不同行业领域的BOM表侧重点不一样。安卓主板的BOM表则侧重点在于元器件物料的清单&#xff0c;也就是安卓电路板的PCBA清单&#xff0c;精密的安卓板有上千个物料&#xff0c;可以帮助我们估算物料成本&#xff0c;建立生产计划&#xff0c…
阅读更多...
Ftp服务器、 Samba服务器、NFS服务器的区别

Ftp服务器、 Samba服务器、NFS服务器的区别

根据使用的方式来看&#xff0c;可以分为3种类别的文件服务器&#xff1a;ftp服务器&#xff08;ftp/tftp&#xff09;、 Samba服务器、NFS服务器。ftp的客户可以是任意平台&#xff0c;samba是专门针对windows客户&#xff0c;而NFS则是面向linux/unix用户的。下面是三种服务器…
阅读更多...
CRM软件系统价格不同的原因

CRM软件系统价格不同的原因

很多人在了解CRM系统时&#xff0c;发现不同品牌的CRM价格有着很大的区别。一些CRM系统只需要几千块钱&#xff0c;一些CRM系统的报价却要上万&#xff0c;甚至十几万。为什么CRM系统价格不同&#xff1f;下面我们就来说说。 1、功能不同 从功能方面来说&#xff0c;一些CRM系…
阅读更多...
OpenCV Series : Slope + Radian + Degree

OpenCV Series : Slope + Radian + Degree

def lineSlope(p1, p2):slope (p2[1] - p1[1]) / (p2[0] - p1[0])return slopedef slopeAngle(p1, p2):slope lineSlope(p1, p2)radian np.arctan(slope)return radiandef angleDegree(radian):theta int(radian * 180 / np.pi) % 360return theta
阅读更多...
【LeetCode热题100】--3.无重复字符的最长子串

【LeetCode热题100】--3.无重复字符的最长子串

3.无重复字符的最长子串 使用滑动窗口&#xff1a; 使用两个指针表示字符串中的某个子串&#xff08;或窗口&#xff09;的左右边界&#xff0c;其中左指针代表着枚举字串的起始位置&#xff0c;而右指针即为 r k r_k rk​在每一步操作中&#xff0c;我们会将左指针向右移动一…
阅读更多...
Python类练习

Python类练习

文章目录 题目要求步骤 题目要求 1)创建一个 Kid 类&#xff0c;包含姓名&#xff0c;性别&#xff0c;年龄属性和 play 方法 2) 创建一个 Stu 类&#xff0c;继承 Kid 类&#xff0c;同时包含成绩属性&#xff0c;获取成绩方法&#xff0c;努力学习方法&#xff0c;play方法&…
阅读更多...
RocketMQ核心编程模型以及生产环境最佳实践

RocketMQ核心编程模型以及生产环境最佳实践

⼀、回顾 RocketMQ 的消息模型 ⼆、深⼊理解 RocketMQ 的消息模型 1 、 RocketMQ 客户端基本流程 RocketMQ 基于 Maven 提供了客户端的核⼼依赖&#xff1a; 使⽤客户端进⾏编程时&#xff0c;添加这⼀个核⼼依赖就够了。 另外还有⼀个与权限控制相关的核⼼依赖也需要了解。尽…
阅读更多...
「聊设计模式」之迭代器模式（Iterator）

「聊设计模式」之迭代器模式（Iterator）

&#x1f3c6;本文收录于《聊设计模式》专栏&#xff0c;专门攻坚指数级提升&#xff0c;助你一臂之力&#xff0c;带你早日登顶&#x1f680;&#xff0c;欢迎持续关注&&收藏&&订阅&#xff01; 前言 设计模式是软件开发中经验的总结&#xff0c;是一种被反复…
阅读更多...
开学季什么触控笔好用又便宜？推荐平价的电容笔

开学季什么触控笔好用又便宜？推荐平价的电容笔

由于iPad平板的强大功能&#xff0c;才让iPad拥有了更多的用户。拿来画画、记笔记什么的体验都是很不错。但是仅仅是拿来看电视、玩游戏&#xff0c;似乎作用不大。如果你不是想要一支昂贵的苹果电容笔&#xff0c;或者只是想要在日常生活中做笔记&#xff0c;那么你可以考虑一…
阅读更多...
springcloud3 分布式事务解决方案seata之TCC模式6

springcloud3 分布式事务解决方案seata之TCC模式6

一 TCC模式 1.1 TCC的逻辑 TCC模式与AT模式非常相似&#xff0c;每阶段都是独立事务&#xff0c;不同的是TCC需要人工干预编写代码。需要实现三个方法&#xff1a; Try&#xff1a;资源的检测和预留&#xff1b; Confirm&#xff1a;完成资源操作业务&#xff1b;要求 Try 成…
阅读更多...
three.js——几何体划分顶点添加不同的材质

three.js——几何体划分顶点添加不同的材质

几何体划分顶点添加不同的材质 前言效果图.addGroup(顶点的下标, 获取几个顶点, 选择材质的下标)在vue中使用 前言 上篇文章讲解了怎样通过索引划分顶点&#xff0c;通过顶点绘制图形,本章通过addGroup方法讲解根据划分的顶点来添加不同的材质 效果图 .addGroup(‘顶点的下标’…
阅读更多...
精品SpringCloud电影院购票系统-微服务-分布式

精品SpringCloud电影院购票系统-微服务-分布式

《[含文档PPT源码等]精品基于SpringCloud实现的电影院购票系统设计的设计与实现-微服务-分布式》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程等 软件开发环境及开发工具&#xff1a; 开发语言&#xff1a;Java 框架&#xff1a;springcloud JDK版…
阅读更多...
【JDK 8-集合框架进阶】6.1 parallelStream 并行流

【JDK 8-集合框架进阶】6.1 parallelStream 并行流

一、parallelStream 并行流 1.1 串行 和 并行的区别 > 执行结果 二、问题 2.1 paralleStream 并行是否一定比 Stream 串行快? 2.2 是否可以都用并行&#xff1f; > 报错 三、实战 > 执行结果 四、总结 一、parallelStream 并行流 多线程并发处理&#xff…
阅读更多...
视频号：平均一场裂变7965人，电商增长玩法全揭秘！

视频号：平均一场裂变7965人，电商增长玩法全揭秘！

我们整理了几何裂变平台上电商行业近3个月的视频号裂变活动&#xff0c;发现用的最多的玩法是粉丝裂变&#xff0c;其次是直播裂变。 平均一场视频号粉丝裂变活动涨粉7965人&#xff0c;裂变层级9级&#xff0c;裂变率872%&#xff0c;即1个老用户能带来8.72个新用户关注视频号…
阅读更多...
数字孪生基础设施需求分析

数字孪生基础设施需求分析

数字孪生基础设施需求分析 “基础设施”&#xff08;infrastructure&#xff09;新型基础设施建设 “基础设施”&#xff08;infrastructure&#xff09; 一词最早于1875年在法文中出现&#xff0c;但该词汇由拉丁文构成&#xff0c;infrastructure分为infra&#xff08;拉丁文…
阅读更多...
汽车电子——产品标准规范汇总和梳理（适应可靠性）

汽车电子——产品标准规范汇总和梳理（适应可靠性）

文章目录 前言 一、电气性能要求 二、机械性能要求 三、气候性能要求 四、材料性能要求 五、耐久性能要求 六、防护性能要求 总结 前言 见《汽车电子——产品标准规范汇总和梳理》 一、电气性能要求 《GB/T 28046.2-2019&#xff08;ISO 16750-2&#xff1a;2012&#…
阅读更多...
算法简述-串和串的匹配、排序、深度/广度优先搜索、动态规划、分治、贪心、回溯、分支限界

算法简述-串和串的匹配、排序、深度/广度优先搜索、动态规划、分治、贪心、回溯、分支限界

目录 算法简述 基本 典型算法列举 串和串的匹配 排序 深度/广度优先搜索 动态规划 分治 贪心 回溯 分支限界 算法简述 基本 咳咳嗯…算法嘛&#xff0c;咱也不是 CS 科班学生&#xff0c;咱就说&#xff0c;算法是对已经建模后的问题的解决的具体途径和方法&#x…
阅读更多...
A-小美种果树（二分）-- 牛客周赛 Round 12

A-小美种果树（二分）-- 牛客周赛 Round 12

输入 1 2 10 输出 6 解析&#xff1a; 二分&#xff0c;注意两端端点L、R的取值&#xff01;&#xff01;&#xff01; #include<bits/stdc.h> using namespace std; #define int long long int x,y,z; signed main(){scanf("%lld%lld%lld",&x,&y,…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023