欢迎关注博主 六月暴雪飞梨花 或加入【六月暴雪飞梨花】一起学习和分享Linux、C、C++、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。

一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。今天就来聊聊这些十分重要的“必抓!”算法吧~
一 引言
1.1 算法的定义
算法是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令。它代表着用系统的方法描述解决问题的策略机制。算法能够处理一定规范的输入,在有限时间内获得所要求的输出。
1.2 算法的特征
一个算法具有以下四个重要的特征:有穷性(Finiteness)、确切性(Definiteness)、输入和输出项 (Input/Ouput)、可行性(Effectiveness)。
1.3 算法的分类
算法可以根据不同的标准进行分类。
- 算法宏观泛义分类:有限确定性算法、有限不定性算法和无限算法。
- 算法设计原理分类:搜索算法、排序算法、图算法、动态规划算法、回溯算法。
- 算法的使用用途分类:数值算法、字符串算法、图像处理算法、机器学习算法、并行计算算法。
1.4 算法的描述
在计算机中,如何描述算法,主要有自然语言,流程图,代码等。
在流程图中,描述算法可使用如下的标识符号。
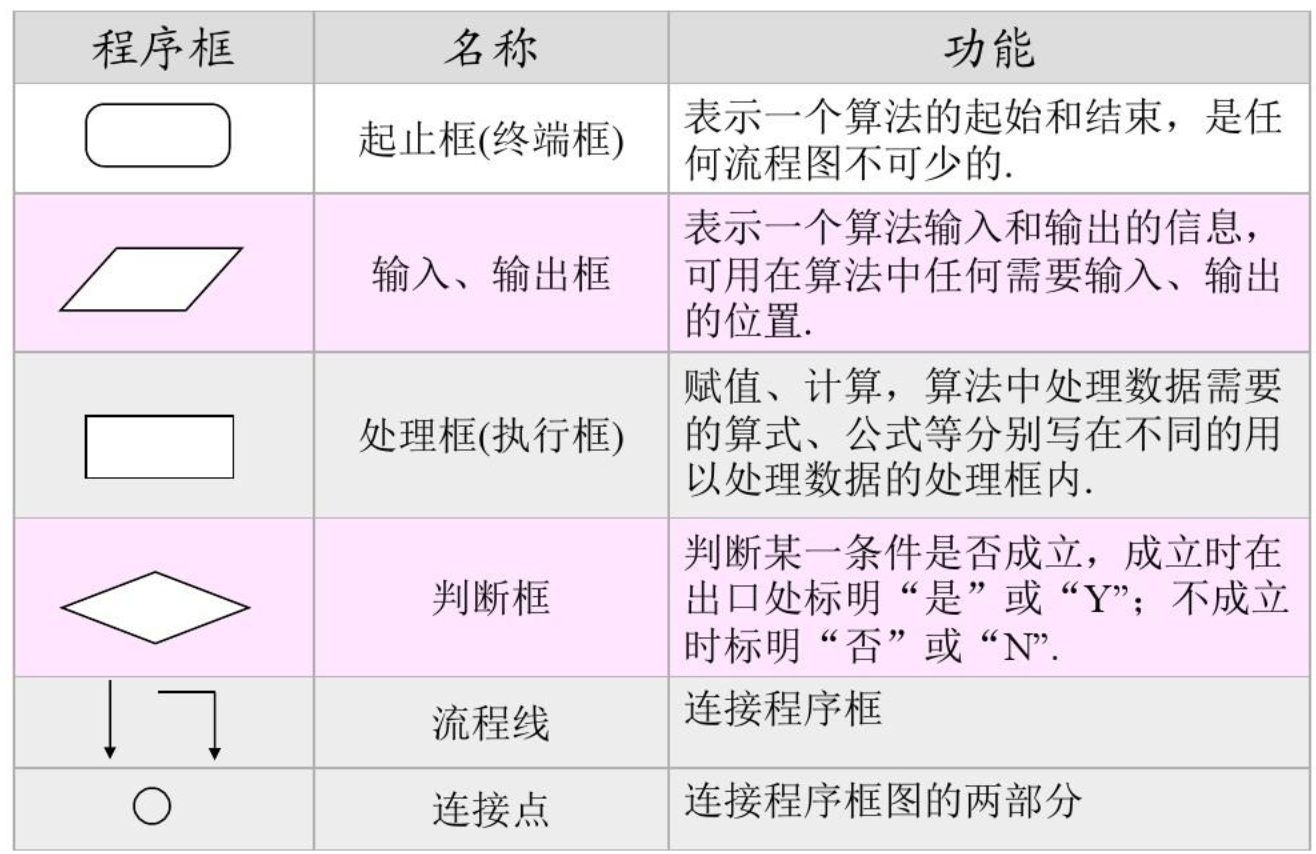
在代码中的算法可以描述为如下
public class RecursionExample {
public static void main(String[] args) {
int n = 5;
int result = factorial(n);
System.out.println("Factorial of " + n + " is " + result);
}
public static int factorial(int n) {
if (n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}
}
使用动态图演示如下:

二 常见算法介绍
提示:介绍常见的排序算法,查找算法、图论算法和字符串算法等等
2.1 分治法
【基本思想】
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
【解题思路】
分解->求解->合并
【实例解析】
快速排序(Quick Sort):选取基准数(比如第一个),比我小的往前排,比我大的往后排。
public class QuickSort {
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
// pi 是分区索引,arr[pi] 的位置已经确定了
int pi = partition(arr, low, high);
// 通过递归调用,分别对pi的左右两部分进行排序
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
// 这个函数用来找出数组中最大元素的位置,并返回该位置
public static int partition(int[] arr, int low, int high) {
// 选择最右边的元素作为基准
int pivot = arr[high];
int i = (low - 1); // 指向最小元素的指针
for (int j = low; j < high; j++) {
// 如果当前元素小于或等于 pivot
if (arr[j] <= pivot) {
i++;
// 交换 arr[i] 和 arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 交换 arr[i+1] 和 arr[high] (或者基准)
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
public static void main(String args[]) {
int arr[] = {10, 7, 8, 9, 1, 5};
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.println("排序后的数组:");
for (int i = 0; i < n; ++i) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
2.2 贪心法
【基本思想】
局部最优解,可能得到整体最优解或是最优解的近似解。
【解题思路】
在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
【实例解析】
Prim算法(最小生成树算法之一,还有一个为Kruskal算法)。
import java.util.Arrays;
class Graph {
private static final int INF = Integer.MAX_VALUE;
private int numVertices;
private int[][] adjacencyMatrix;
public Graph(int numVertices) {
this.numVertices = numVertices;
adjacencyMatrix = new int[numVertices][numVertices];
for (int[] row : adjacencyMatrix)
Arrays.fill(row, INF);
}
public void addEdge(int src, int dest, int weight) {
adjacencyMatrix[src][dest] = weight;
adjacencyMatrix[dest][src] = weight;
}
private int getMinVertex(boolean[] mstSet, int[] key) {
int minKey = INF;
int vertex = -1;
for (int i = 0; i < numVertices; i++) {
if (!mstSet[i] && key[i] < minKey) {
minKey = key[i];
vertex = i;
}
}
return vertex;
}
public void primMST() {
boolean[] mstSet = new boolean[numVertices];
int[] key = new int[numVertices];
int[] parent = new int[numVertices];
Arrays.fill(key, INF);
Arrays.fill(parent, -1);
key[0] = 0;
for (int i = 0; i < numVertices - 1; i++) {
int minVertex = getMinVertex(mstSet, key);
mstSet[minVertex] = true;
for (int j = 0; j < numVertices; j++) {
int edgeWeight = adjacencyMatrix[minVertex][j];
if (edgeWeight != INF && !mstSet[j] && edgeWeight < key[j]) {
parent[j] = minVertex;
key[j] = edgeWeight;
}
}
}
printMST(parent, key);
}
private void printMST(int[] parent, int[] key) {
System.out.println("Edge \tWeight");
for (int i = 1; i < numVertices; i++)
System.out.println(parent[i] + " - " + i + "\t" + key[i]);
}
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1, 2);
graph.addEdge(0, 3, 6);
graph.addEdge(1, 2, 3);
graph.addEdge(1, 3, 8);
graph.addEdge(1, 4, 5);
graph.addEdge(2, 4, 7);
graph.addEdge(3, 4, 9);
graph.primMST();
}
1.3 分支限界法
【基本思想】
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
【解题思路】
找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解.
【实例解析】
优先队列式分支限界法。
import java.util.PriorityQueue;
public class BranchAndBound {
// 定义节点类
static class Node implements Comparable<Node> {
int level; // 节点层数
int cost; // 节点代价
boolean isLeaf; // 是否为叶子节点
Node(int level, int cost, boolean isLeaf) {
this.level = level;
this.cost = cost;
this.isLeaf = isLeaf;
}
// 根据节点优先级进行比较
public int compareTo(Node other) {
return Integer.compare(cost, other.cost);
}
}
// 优先队列式分支限界法
public static void branchAndBound(Node root) {
PriorityQueue<Node> queue = new PriorityQueue<>(); // 创建优先队列
queue.offer(root); // 将根节点加入队列中
while (!queue.isEmpty()) {
Node node = queue.poll(); // 选择优先级最高的节点作为当前扩展节点
if (node.isLeaf) {
// 如果当前扩展节点是目标节点,则算法结束
System.out.println("目标节点找到!");
break;
} else {
// 对当前扩展节点进行扩展,生成所有子节点,并将它们加入优先队列中
for (int i = 0; i < 2; i++) {
int level = node.level + 1;
int cost = node.cost + i;
boolean isLeaf = (i == 1); // 假设只有一个叶子节点
Node child = new Node(level, cost, isLeaf);
queue.offer(child); // 将子节点加入队列中
}
}
}
}
public static void main(String[] args) {
int level = 0; // 根节点层数为0
int cost = 0; // 根节点代价为0
boolean isLeaf = false; // 根节点不是叶子节点
Node root = new Node(level, cost, isLeaf); // 创建根节点
branchAndBound(root); // 运行分支限界法算法
}
}
三 重点算法总结
3.1 算法的应用场景
算法是解决特定问题或执行特定任务的一组明确的步骤。
- 排序算法:主要应用在计算机科学中,排序算法用于将一组数据按照特定的顺序(例如升序或降序)排列。
- 搜索算法:搜索算法用于在数据结构(如数组,链表,树等)中查找特定的元素。这些算法在互联网搜索引擎,数据库系统,文件管理系统等场景中有着广泛的应用。
- 机器学习算法:从大量数据中提取有用的模式,并做出预测或决策。它们广泛应用于图像和语音识别,推荐系统,预测分析,自动驾驶等领域。
- 加密算法:在网络安全领域,加密算法用于保护数据的机密性和完整性。这些算法广泛用于电子商务,电子银行,远程办公等场景。
- 图算法:图算法用于处理图形结构数据,如社交网络、互联网路由、交通网络等。它们在这些复杂网络中寻找路径、检测环路、计算距离等问题。
3.2 如何学习和掌握算法
算法是计算机科学的基础,它们对于解决复杂问题,优化解决方案以及提高程序性能至关重要。
学习算法是一个循序渐进的过程。
- 个人可以定期进行算法培训、参加算法挑战项目(在参战过程中获取奖励和认可)。
- 机构和企业鼓励员工参加算法竞赛、建立算法基金支持,为那些对算法有深入研究愿望的程序员提供一定的资金支持,这样可以鼓励他们深入研究,发表高质量的研究成果。
- 最后,共同推广常用算法以及应用。