1.牛顿万有引力定律

艾萨克·牛顿爵士的万有引力定律，通常简称为牛顿万有引力定律，是物理学的基本原理。牛顿于 1687 年在其开创性著作《Philosophiæ Naturalis Principia Mathematica》（自然哲学的数学原理）中发表了这一定律。

该定律指出，宇宙中的每个物体都以与它们质量的乘积成正比、与它们中心之间的距离的平方成反比的力吸引所有其他物体。在数学上，这表示为

其中F代表引力，G是引力常数（大约6.67430 x 10-11 m3 kg-1 s-2），m₁和m2是两个物体的质量，r是它们中心之间的距离。

它为理解地球和天体力学提供了一个统一的框架，证明导致物体落在地球上的同一力也控制着天体的运动。

2. 爱因斯坦的能量质量等价

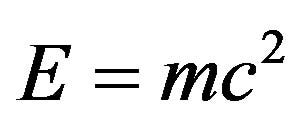
该方程表明，能量与物体在其静止坐标系中的质量成正比，光速的平方充当方程中的巨大常数。由于这个常数的巨大值，即使是少量的质量在转换时也能产生惊人的大量能量。

1905 年，爱因斯坦发表了被认为是他历史上最重要的研究论文，题为“Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?” 或“身体的惯性是否取决于其能量含量？”。他几乎不知道这篇论文会产生深远的影响，包括第二次世界大战期间导致超过 20 万日本人死亡的悲惨事件。在他的开创性工作中，爱因斯坦解释了质量和能量的等价性，证明它们是相互关联的，并且可以从一种形式转换为另一种形式。

3. 薛定谔方程

薛定谔方程是量子力学的基础方程，由奥地利物理学家埃尔文·薛定谔于 1925 年提出。它描述了电子和原子等量子系统的行为，在理解其波状性质方面发挥着核心作用。该方程是一个偏微分方程，它将量子态的时间演化与其空间属性和能量联系起来。

在其与时间相关的形式中，薛定谔方程可写为：

其中 i 是虚数单位，ħ 是简化的普朗克常数，∂ψ/∂t 表示波函数 ψ 的时间导数，m 是粒子的质量，∇² 是描述空间变化的拉普拉斯算子，V 是势能函数，ψ 是波函数本身，它编码有关量子系统的信息。

求解薛定谔方程可得到波函数 ψ，它可以完整地描述量子系统的行为。波函数绝对值的平方|ψ|²给出了找到处于特定位置或动量状态的粒子的概率密度。

它为广泛的应用铺平了道路，从理解原子和分子的行为到开发量子计算和量子密码学等量子技术。

4.麦克斯韦方程组

麦克斯韦方程组是电磁学中的四个基本方程组，由詹姆斯·克拉克·麦克斯韦在 19 世纪提出。它们描述了存在电荷和电流时电场和磁场的行为。

这些方程是高斯电定律，指出通过封闭表面的电通量与封闭的电荷成正比。

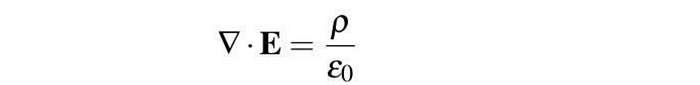
高斯磁力定律，该定律指出磁单极子不存在。

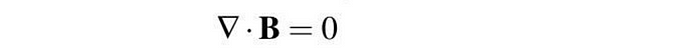
法拉第电磁感应定律将变化的磁场与感应电场联系起来。

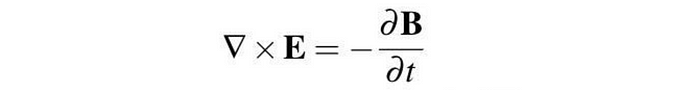
安培定律与麦克斯韦加法，将磁场循环与电流和位移电流联系起来。

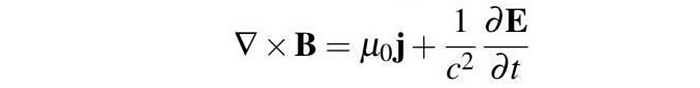
这些方程共同揭示了电场和磁场之间复杂的关系以及它们与电荷和电流的相互作用。它们支撑着经典电磁学，为理解电磁波、无线电波和电路行为提供了基础。此外，麦克斯韦方程组在现代通信系统、电气工程和狭义相对论的发展中发挥了至关重要的作用。它们的优雅和预测能力使它们成为电磁学在各个科学技术领域的研究和应用中不可或缺的工具。

5.热力学第二定律

热力学第二定律是物理学的基本原理，涉及熵的概念和自然过程的方向。

它指出，在封闭系统中，总熵（无序性或随机性的度量）往往会随着时间的推移而增加。简单来说，它描述了许多自然过程的不可逆性质以及系统走向更加无序状态的趋势。

熵的增加与传热和能量流的概念有关。当能量从较热的物体转移到较冷的物体时，部分能量会以热量的形式耗散，从而增加系统的熵。随着时间的推移，这会导致温度均衡并建立热平衡。

尽管封闭系统中的总能量是守恒的，但可用于做有用功的能量随着熵的增加而减少。这就引出了“时间之箭”的概念，因为某些过程是不可逆的，只能朝一个方向移动。

虽然熵的局部减少是可能的（例如，晶体的形成），但它们总是伴随着其他地方的熵的更大增加。热力学第二定律为物理系统的行为、能量转换的局限性以及宇宙本身的最终命运提供了重要的见解。

6.普朗克方程

该方程也称为普朗克定律，是量子物理学的基础，由德国物理学家马克斯·普朗克于 1900 年提出。它描述了黑体发出的辐射的光谱分布，黑体是一个理想化的物体，可以完美地吸收和发射所有入射辐射在上面。

其中E是光子的能量，h是普朗克常数，v是光子的频率，c是光速。

普朗克方程标志着量子理论的诞生，因为它引入了能量量子化的概念。普朗克假设电磁能只能以离散的能量包或“量子”的形式发射或吸收，而不是连续的。这个想法为量子力学的发展奠定了基础。

普朗克定律成功地解释了观察到的黑体在各种波长和温度范围内发射的能量分布，克服了经典物理学的缺点。它在理解各种现象（包括宇宙微波背景辐射以及原子和分子的行为）方面发挥了至关重要的作用。而且，它对后来量子力学和量子场论的发展做出了重大贡献，成为现代物理学的基石。

7.牛顿第二运动定律

牛顿第二运动定律是经典力学的基本原理，由艾萨克·牛顿爵士于 17 世纪提出。它指出物体的加速度与作用在其上的合力成正比，与其质量成反比。

在数学上，它表示为，

其中 F 表示施加到物体上的净力，m 是物体的质量，a 是由此产生的加速度。

该定律强调了力与运动之间的因果关系。当不平衡力作用于物体时，物体会沿力的方向加速。施加的力越大，产生的加速度就越大。相反，质量较大的物体需要更大的力才能达到与较轻的物体相同的加速度。

牛顿第二定律具有广泛的应用，对于理解和预测物体在各种情况下的行为至关重要。它解释了从下落的苹果到绕轨道运行的行星等一切物体的运动。此外，该定律构成了工程的基础，使结构、车辆和机器的设计和分析成为可能。

8.波动方程

波动方程是一个基本的偏微分方程，描述了各个科学领域中类波现象的行为。它用于模拟各种物理系统，包括声音、光和电磁波。

一维形式的波动方程由下式给出：

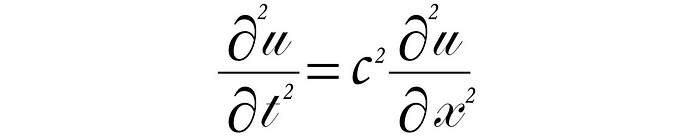
其中u(x, t)表示波在位置x和时间t处的位移，c是波速。该方程断言波的位移对时间的二阶导数 (∂²u/∂t²) 与位移对位置的二阶导数 (∂²u/∂x²) 成正比，其中 c² 是比例常数。

波动方程保证了波以恒定的速度c传播，并且表现出波的干涉、衍射、反射等特征性质。求解波动方程可得到描述波在空间和时间中如何演化的波动解。

波动方程在物理、工程和其他学科中有着广泛的应用。它在声学中用于研究声波和振动，在光学中用于分析光传播，在电磁学中用于理解电磁波。此外，它在地震学、信号处理和电信等各个领域也发挥着重要作用。

通过提供对波动现象的严格数学描述，波动方程已成为理解和预测波动行为不可或缺的工具，推动了许多技术和科学领域的进步。

9.爱因斯坦场方程

爱因斯坦场方程是 1915 年提出的爱因斯坦广义相对论的基石。该方程使用张量表示法隐藏了 10 个偏微分方程。

用数学术语来说，方程可以表示为：

其中Gμν代表爱因斯坦张量，编码时空曲率，G是引力常数，c是光速，Tμν是应力-能量张量，描述宇宙中物质和能量的分布。

这些方程将时空的几何形状与质量和能量的存在联系起来。从本质上讲，它们揭示了质量和能量扭曲了它们周围的时空结构，导致附近的物体遵循弯曲的路径，我们将其视为重力。

爱因斯坦场方程带来了对宇宙的非凡见解。他们成功地解释了水星轨道的进动、大质量物体周围光线的弯曲（引力透镜）以及黑洞的存在。此外，它们是宇宙学的基础，描述了宇宙的膨胀和大规模结构的形成。

10.狄拉克方程

狄拉克方程是量子力学和相对论量子场论中的一个基本方程，由英国物理学家保罗·狄拉克于 1928 年提出。它描述了费米子（例如电子）在相对论背景下的行为，同时考虑了量子力学和狭义相对论。

在数学上，狄拉克方程如下：

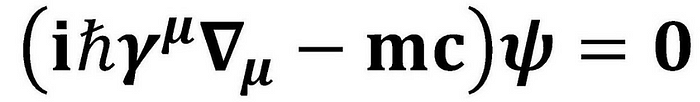
其中ψ表示费米子波函数，γ^μ是一组称为狄拉克伽玛矩阵的4x4矩阵，Δμ是四梯度算子，m是费米子的静止质量，c是真空中的光速。

狄拉克方程预测了自旋 1/2 粒子的存在，这是物质的基本组成部分。它成功地解释了电子自旋、原子光谱的精细结构以及强电磁场中粒子的行为等现象。

狄拉克方程的一个重要推论是反物质的预测。狄拉克的工作揭示了该方程允许具有正能量和负能量的解，从而导致了反粒子的理论预测，例如正电子（电子的反粒子）。

狄拉克方程是量子场论公式中的关键要素，特别是在粒子物理标准模型的发展中。

11.洛伦兹变换

洛伦兹变换是爱因斯坦狭义相对论中的基本方程。它们描述了从不同的移动参考系观察时，特别是当物体接近光速时，空间和时间的测量如何变化。

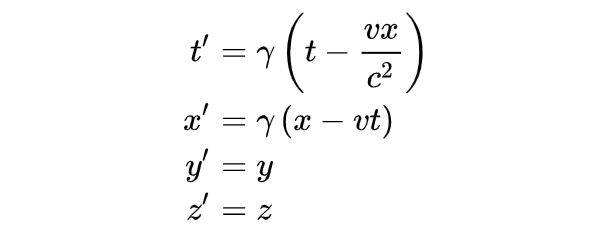
其中 ( t , x , y , z ) 和 ( t ', x ', y ', z ') 是两个帧中事件的坐标，原点在t = t '=0处重合，其中初始化帧是从未涂底漆的框架中可以看出，其沿x轴以速度v移动。

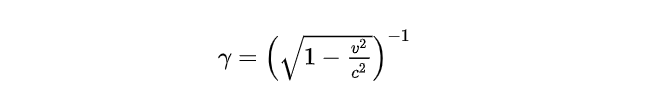
20 世纪初，物理学家亨德里克·洛伦兹导出了这些变换，以协调麦克斯韦方程组与伽利略相对论。阿尔伯特·爱因斯坦后来将它们作为其革命性狭义相对论的关键组成部分。

洛伦兹变换涉及两个主要因素：时间膨胀和长度收缩。他们证明，随着物体速度的增加，相对于静止的观察者，时间似乎会变慢，并且其长度沿着运动方向显得更短。当物体的速度接近光速时，这些效应变得更加明显，时间似乎停止了，长度收缩为零。

洛伦兹变换还将空间和时间统一到四维时空框架中。这使得光速在所有参考系中都保持为绝对常数，从而得出显着的结论，例如同时性的相对性以及质量和能量的等价性 (E=mc²)。

它们在各个领域发挥着至关重要的作用，包括粒子物理学、宇宙学以及 GPS 系统等技术的开发，在这些领域中，必须考虑相对论效应才能进行精确测量。

12.玻尔兹曼熵

玻尔兹曼熵以奥地利物理学家路德维希·玻尔兹曼的名字命名，是统计力学中的一个基本概念，它在微观层面上量化物理系统的无序性或随机性水平。它是对系统在保持相同宏观属性（例如能量或温度）的同时可以占据的不同可能微观状态数量的度量。

高度有序或低熵系统具有较少的可能微观状态，而无序或高熵系统具有大量微观状态。

玻尔兹曼熵的公式由下式给出

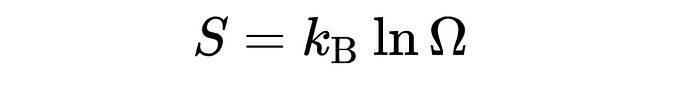
其中 S 是熵，k 是玻尔兹曼常数，Ω 是与给定宏观状态对应的微观状态的数量。

玻尔兹曼熵的概念已被用于理解物理、化学甚至信息论中的各种现象。它有助于解释气体的行为、相变的本质以及热力学中不可逆的概念。

玻尔兹曼熵最重要的贡献之一是它与热力学第二定律的联系，该定律指出封闭系统的总熵总是随着时间的推移而增加。这种关联强调了物理系统向更高无序和更大熵状态演化的不可阻挡的趋势，为我们理解时间之箭和自然过程中不可逆的概念提供了基础。

13.海森堡测不准原理

海森堡测不准原理是量子力学中的一个基本概念，以德国物理学家维尔纳·海森堡 (Werner Heisenberg) 的名字命名，他于 1927 年提出了该原理。它指出，在精确度上存在固有的限制，在精确度上，可以同时知道某些互补变量对的精确度。量子系统。

该原理通常以位置-动量不确定性关系为例。它指出，人们试图测量粒子的位置越准确，确定其动量的准确度就越低，反之亦然。从数学上来说，

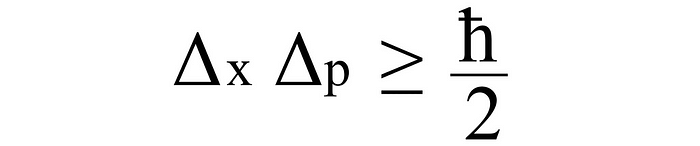
其中 Δx 表示位置的不确定性，Δp 是动量的不确定性，ħ 是简化的普朗克常数。

它强调了量子系统固有的概率性质，其中测量行为本身会扰乱粒子的状态，使得同时无法获得位置和动量的精确知识。

14.哈勃定律

哈勃定律是宇宙学的基本原理，以美国天文学家埃德温·哈勃 (Edwin Hubble) 的名字命名，他在 20 年代做出了开创性的观测。它描述了星系距地球的距离与其红移之间的关系，红移是衡量星系的光如何因宇宙膨胀而向更长波长移动的指标。

哈勃定律在数学上表达为：

其中“v”是星系的退行速度（通过其红移测量），“H₀”是哈勃常数（代表宇宙膨胀的速率），“d”是星系距地球的距离。这种简单的线性关系意味着星系离我们越远，它离开我们的速度就越快。

哈勃定律的发现彻底改变了宇宙学，并为大爆炸理论提供了强有力的证据，支持了宇宙从炽热而致密的初始状态膨胀的观点。它还引发了宇宙膨胀的概念，并认识到空间本身正在拉伸，导致星系彼此远离。

哈勃定律对于我们理解宇宙的过去、现在和未来有着深远的影响。哈勃常数是该定律中的一个关键参数，多年来不断完善，塑造了我们对宇宙年龄和大小的认识。

15.纳维-斯托克斯方程

纳维-斯托克斯方程是流体动力学中的一组偏微分方程，用于描述流体物质（例如气体和液体）的运动。它们以法国数学家和物理学家克劳德·路易斯·纳维和爱尔兰数学家乔治·加布里埃尔·斯托克斯的名字命名，他们在 19 世纪独立提出了它们。

这些方程以数学方式表达了流体中动量和质量的守恒。它们描述了流体的速度场如何随时间演变，同时考虑了流体的粘度、密度以及压力和重力等外力。

纳维-斯托克斯方程可以用向量形式表示为：

纳维-斯托克斯方程对于理解各种流体现象至关重要，从河流和海洋中的水流到大气中气流的动力学。它们在空气动力学、天气预报、海洋学和工程等各个领域都有应用。

尽管纳维-斯托克斯方程具有根本重要性，但在大多数实际情况下解析求解纳维-斯托克斯方程极具挑战性。在许多情况下，数值方法和计算流体动力学 (CFD) 技术用于近似解决方案并深入了解流体行为。