深度学习——所需知识二

---

前言

书接上章，本章将继续介绍一下学习深度学习前要掌握的知识：微积分、自动微分、概率。[d2l库是《动手学深度学习》这本书的配套代码库，它提供了一系列用于深度学习的实用工具和实现示例]
参考书：
《动手学深度学习》

---

一、微积分

微积分分为积分和微分，在微分学中最重要的应用是优化问题，即考虑如何把事情做到最好。

在深度学习中，我们“训练”模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。 通常情况下，变得更好意味着最小化一个损失函数（loss function）。

我们可以将拟合模型的任务分解为两个关键问题：

1. 优化（optimization）：用模型拟合观测数据的过程；
2. 泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

1.1. 导数和微分

导数的计算，这是几乎所有深度学习优化算法的关键步骤。 在深度学习中，我们通常选择对于模型参数可微的损失函数。
假设我们有一个函数f，其输入和输出都是标量。 如果f的导数存在，这个极限被定义为：

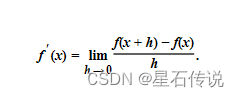
定义u=f(x)=3x²−4x如下，通过令x=1并让h接近0

def f(x):
    return 3*x**2 - 4*x
def numerical_lim(f,x,h):
    return (f(x+h) - f(x)) / h
h = 0.1
for i in range(5):
    print(f"h={h:.5f},numerical limit = {numerical_lim(f,1,h):.5f}")
    h *= 0.1


#结果：
h=0.10000,numerical limit = 2.30000
h=0.01000,numerical limit = 2.03000
h=0.00100,numerical limit = 2.00300
h=0.00010,numerical limit = 2.00030
h=0.00001,numerical limit = 2.00003

当x=1时，导数u′是2。其实导数可视为曲线$u=f(x)$切线的斜率。

进行可视化：

import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l

def f(x):
    return 3 * x ** 2 - 4 * x


def use_svg_display():  # @save
    """使用svg格式在Jupyter中显示绘图"""
    backend_inline.set_matplotlib_formats('svg')


def set_figsize(figsize=(3.5, 2.5)):  # @save
    """设置matplotlib的图表大小"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize


# @save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()


# @save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

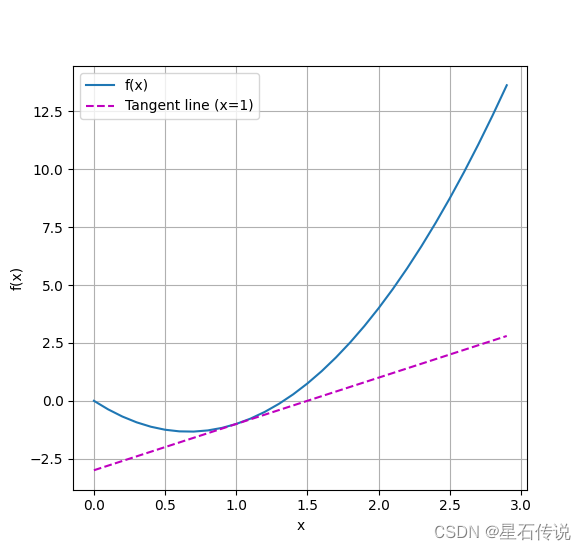
成功绘制函数$u=f(x)$及其在$x=1$处的切线$y=2x-3$，其中系数$2$是切线的斜率。

1.2. 偏导数

到目前为止，我们只讨论了仅含一个变量的函数的微分。
在深度学习中，函数通常依赖于许多变量。
因此，我们需要将微分的思想推广到多元函数

$$\frac{\partial y}{\partial x_i}=\underset{h\to 0}{\lim }\frac{f(x_1,\dots ,x_{i-1},x_i+h,x_{i+1},\dots ,x_n)-f(x_1,\dots ,x_i,\dots ,x_n)}{h}.$$

为了计算$\frac{\partial y}{\partial x_i}$，
我们可以简单地将$x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n$看作常数，
并计算$y$关于$x_i$的导数

1.3. 梯度

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。函数$f(\mathbf{x})$相对于$\mathbf{x}$的梯度是一个包含$n$个偏导数的向量:

$${\nabla }_{\mathbf{x}}f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_n}{]}^{\top },$$

1.4. 链式法则

然而，上面方法可能很难找到梯度。
这是因为在深度学习中，多元函数通常是复合（composite）的，
所以难以应用上述任何规则来微分这些函数。
幸运的是，链式法则可以被用来微分复合函数。

假设可微分函数$y$有变量$u_1,u_2,\dots ,u_m$，其中每个可微分函数$u_i$都有变量$x_1,x_2,\dots ,x_n$。
注意，$y$是$x_1,x_2，\dots ,x_n$的函数。
对于任意$i=1,2,\dots ,n$，链式法则给出：

$$\frac{\partial y}{\partial x_i}=\frac{\partial y}{\partial u_1}\frac{\partial u_1}{\partial x_i}+\frac{\partial y}{\partial u_2}\frac{\partial u_2}{\partial x_i}+\cdots +\frac{\partial y}{\partial u_m}\frac{\partial u_m}{\partial x_i}$$

二、自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。

2.1. 简单例子

假设我们想对函数$y=2x^{T}x$关于列向量x求导

#1.2.偏导数
import torch
x = torch.arange(4.0)
print(x)
x.requires_grad_(True)	# 等价于x=torch.arange(4.0,requires_grad=True)
print(x.grad)	#默认值是None
y = 2 * torch.dot(x,x)
#通过调用反向传播函数来自动计算`y`关于`x`每个分量的梯度
y.backward()
print(x.grad)
print(x.grad == 4*x)
# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值(计算x的另一个函数）
x.grad.zero_()
y = x.sum()
y.backward()
print(x.grad)


#结果:
tensor([0., 1., 2., 3.])
None
tensor([ 0.,  4.,  8., 12.])
tensor([True, True, True, True])
tensor([1., 1., 1., 1.])

2.2. 非标量变量的反向传播

当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。
对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

# 对非标量调用backward需要传入一个gradient参数，该参数指定微分函数关于self的梯度。
# 本例只想求偏导数的和，所以传递一个1的梯度是合适的
x.grad.zero_()
print(x)
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
print(x.grad)


#结果：
tensor([0., 1., 2., 3.], requires_grad=True)
tensor([0., 2., 4., 6.])

2.3. 分离计算

有时，我们希望将某些计算移动到记录的计算图之外
下面的反向传播函数计算z=ux关于x的偏导数，同时将u作为常数处理， 而不是z=xx*x关于x的偏导数。

#分离计算
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
print(x.grad)
print(x.grad == u)

x.grad.zero_()
y.sum().backward()
print(x.grad == 2 * x)



#结果：
tensor([0., 1., 4., 9.])
tensor([True, True, True, True])
tensor([True, True, True, True])

2.4. python控制流的梯度计算

即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度

#python控制流的梯度计算
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
print(a.grad == d / a)


#结果：
tensor(True)

我们现在可以分析上面定义的f函数。 请注意，它在其输入a中是分段线性的。 换言之，对于任何a，存在某个常量标量k，使得f(a)=k*a，其中k的值取决于输入a，因此可以用d/a验证梯度是否正确。

三、概率

简单地说，机器学习就是做出预测。

3.1. 基本概率论

假设我们掷骰子，想知道看到1的几率有多大。
如果骰子是公平的，那么所有六个结果 { 1 , … , 6 } \{1, \ldots, 6\} {1,…,6}都有相同的可能发生，因此我们可以说$1$发生的概率为$\frac{1}{6}$。
大数定律 告诉我们：随着投掷次数的增加，这个估计值会越来越接近真实的潜在概率。

#概率：
import torch
from torch.distributions import multinomial
from d2l import torch as d2l
fair_probs = torch.ones([6]) / 6
print(fair_probs)
#出现次数
print(multinomial.Multinomial(1, fair_probs).sample())
print(multinomial.Multinomial(10, fair_probs).sample())
# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(2000, fair_probs).sample()
print(counts / 2000)  # 相对频率作为估计值


#结果：
tensor([0.1667, 0.1667, 0.1667, 0.1667, 0.1667, 0.1667])
tensor([1., 0., 0., 0., 0., 0.])
tensor([1., 1., 2., 2., 2., 2.])
tensor([0.1745, 0.1620, 0.1630, 0.1675, 0.1650, 0.1680])

因为我们是从一个公平的骰子中生成的数据，我们知道每个结果都有真实的概率$\frac{1}{6}$，大约是$0.167$，所以上面输出的估计值看起来不错。

​我们也可以看到这些概率如何随着时间的推移收敛到真实概率。
让我们进行500组实验，每组抽取10个样本：
​

counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)

d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()
d2l.plt.show()

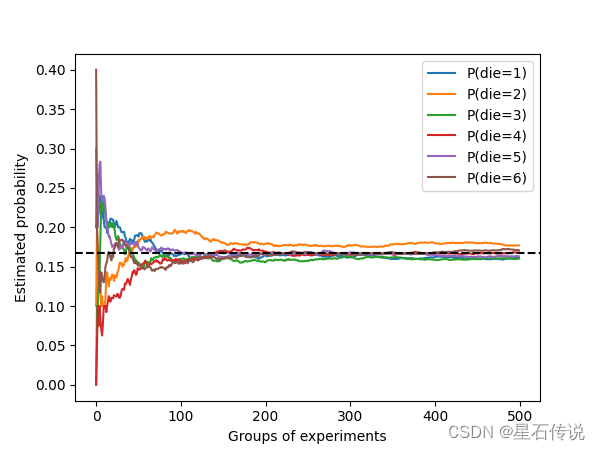
每条实线对应于骰子的6个值中的一个，并给出骰子在每组实验后出现值的估计概率。
当我们通过更多的实验获得更多的数据时，这$6$条实体曲线向真实概率收敛。

3.1.1. 概率论公理

在处理骰子掷出时，我们将集合 S = { 1 , 2 , 3 , 4 , 5 , 6 } \mathcal{S} = \{1, 2, 3, 4, 5, 6\} S={1,2,3,4,5,6}
称为样本空间（sample space）或结果空间（outcome space），
其中每个元素都是结果（outcome）。
事件（event）是一组给定样本空间的随机结果。

概率（probability）可以被认为是将集合映射到真实值的函数。在给定的样本空间$\mathcal{S}$中，事件$\mathcal{A}$的概率，表示为$P(\mathcal{A})$

3.1.2. 随机变量

在我们掷骰子的随机实验中，我们引入了随机变量（random variable）的概念。随机变量几乎可以是任何数量，并且它可以在随机实验的一组可能性中取一个值。

离散（discrete）随机变量（如骰子的每一面）
和连续（continuous）随机变量（如人的体重和身高）之间存在区别。

3.2. 处理多个随机变量

很多时候，我们会考虑多个随机变量。例如：

图像包含数百万像素，因此有数百万个随机变量。
在许多情况下，图像会附带一个标签（label），标识图像中的对象。
我们也可以将标签视为一个随机变量。
我们甚至可以将所有元数据视为随机变量，例如位置、时间、光圈、焦距、ISO、对焦距离和相机类型。
所有这些都是联合发生的随机变量。
当我们处理多个随机变量时，会有若干个变量是我们感兴趣的。

3.2.1.联合概率

第一个被称为联合概率（joint probability）$P(A=a,B=b)$。
给定任意值$a$和$b$，联合概率可以回答：$A=a$和$B=b$同时满足的概率是多少？
请注意，对于任何$a$和$b$的取值，$P(A=a,B=b)\le P(A=a)$。

3.2.2. 条件概率

联合概率的不等式带给我们一个有趣的比率：
$0\le \frac{P(A=a,B=b)}{P(A=a)}\le 1$。
我们称这个比率为条件概率（conditional probability），
并用$P(B=b\mid A=a)$表示它：它是$B=b$的概率，前提是$A=a$已发生。

3.2.3. 贝叶斯定理

基于条件概率的定义
根据乘法法则可得到$P(A,B)=P(B\mid A)P(A)$。
根据对称性，可得到$P(A,B)=P(A\mid B)P(B)$。
假设$P(B)>0$，求解其中一个条件变量，我们得到

$$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}.$$

请注意，这里我们使用紧凑的表示法：
其中$P(A,B)$是一个联合分布（joint distribution），
$P(A\mid B)$是一个条件分布（conditional distribution）。
这种分布可以在给定值$A=a,B=b$上进行求值。

3.2.4. 边际化

为了能进行事件概率求和，我们需要求和法则
即$B$的概率相当于计算$A$的所有可能选择，并将所有选择的联合概率聚合在一起：

$$P(B)=\sum _{A}P(A,B),$$

这也称为边际化（marginalization）。
边际化结果的概率或分布称为边际概率（marginal probability）
或边际分布（marginal distribution）。

3.2.5. 独立性

如果两个随机变量$A$和$B$是独立的，意味着事件$A$的发生跟$B$事件的发生无关。
在这种情况下，统计学家通常将这一点表述为$A\perp B$。
根据贝叶斯定理，马上就能同样得到$P(A\mid B)=P(A)$。
在所有其他情况下，我们称$A$和$B$依赖。

由于$P(A\mid B)=\frac{P(A,B)}{P(B)}=P(A)$等价于$P(A,B)=P(A)P(B)$，
因此两个随机变量是独立的，当且仅当两个随机变量的联合分布是其各自分布的乘积。
同样地，给定另一个随机变量$C$时，两个随机变量$A$和$B$是条件独立的
当且仅当$P(A,B\mid C)=P(A\mid C)P(B\mid C)$。
这个情况表示为$A\perp B\mid C$。

3.3. 期望和方差

为了概括概率分布的关键特征，我们需要一些测量方法。
一个随机变量$X$的期望（expectation，或平均值（average））表示为

$$E[X]=\sum _{x}xP(X=x).$$

在许多情况下，我们希望衡量随机变量$X$与其期望值的偏置。这可以通过方差来量化

$$\mathrm{Var}[X]=E\left[(X-E[X]{)}^2\right]=E[X^2]-E[X{]}^2.$$

随机变量函数的方差衡量的是：当从该随机变量分布中采样不同值$x$时，
函数值偏离该函数的期望的程度：

$$\mathrm{Var}[f(x)]=E\left[{\left(f(x)-E[f(x)]\right)}^2\right].$$

四、查阅文档

4.1. 查找模块中所有函数和类

为了知道模块中可以调用哪些函数和类，可以调用dir函数

import torch
print(dir(torch))

4.2. 查找特定函数和类的用法

有关如何使用给定函数或类的更具体说明，可以调用help函数查看

print(help(torch.zeros_like))

---

总结

本章详细介绍了学习深度学习前要掌握的知识：微积分、自动微分、概率。接下来将正式开始深度学习的学习，下一章将是有关线性神经网络的讲解。

夫唯不居，是以不去。

–2023-9-17 进阶篇