1:如何建堆(两种方法)

2:两种方法建堆的时间复杂度分析与计算

3:不同类型的排序方式我们应该如何建堆

文章正式开始：

1：如何建堆

在实现堆排序之前我们必须得建堆，才能够实现堆排序

首先在讲解如何建堆之前让我们先来回顾一下堆的概念，堆是一种完全二叉树，它有两种形式，一种是大根堆，另外一种是小根堆。

大根堆：所有的父亲结点大于或等于孩子结点。

小根堆：所有的父亲结点小于或等于孩子结点。

本文在介绍堆排序的时候我们都默认排升序。

方法1：我们采用向上调整算法建堆

我们知道向上调整算法的前提是前面的数必须是堆，所以我们就形成了一种思路：

第一个数我们可以看成是一个堆，那么从第二个数开始我们就依次采用向上调整算法，这样最后我们的数字就会形成一个堆。

图解：

向上调整建堆的代码如下，如果不理解可以自己尝试画图：

//假设排升序，建大堆
void HeapSort(int* a, int n)
 {
	//先建堆,用向上调整算法
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
    }
 }

方法2：采用向下调整的思路建堆

向下调整的前提：要调整的对象左右子树都得是堆

那么我们如何通过一个数组来原地建堆呢？

其实我们可以这样想，叶子结点既可以看作是大堆，也可以看作是小堆，所以我们可以从后面往前面来建堆。

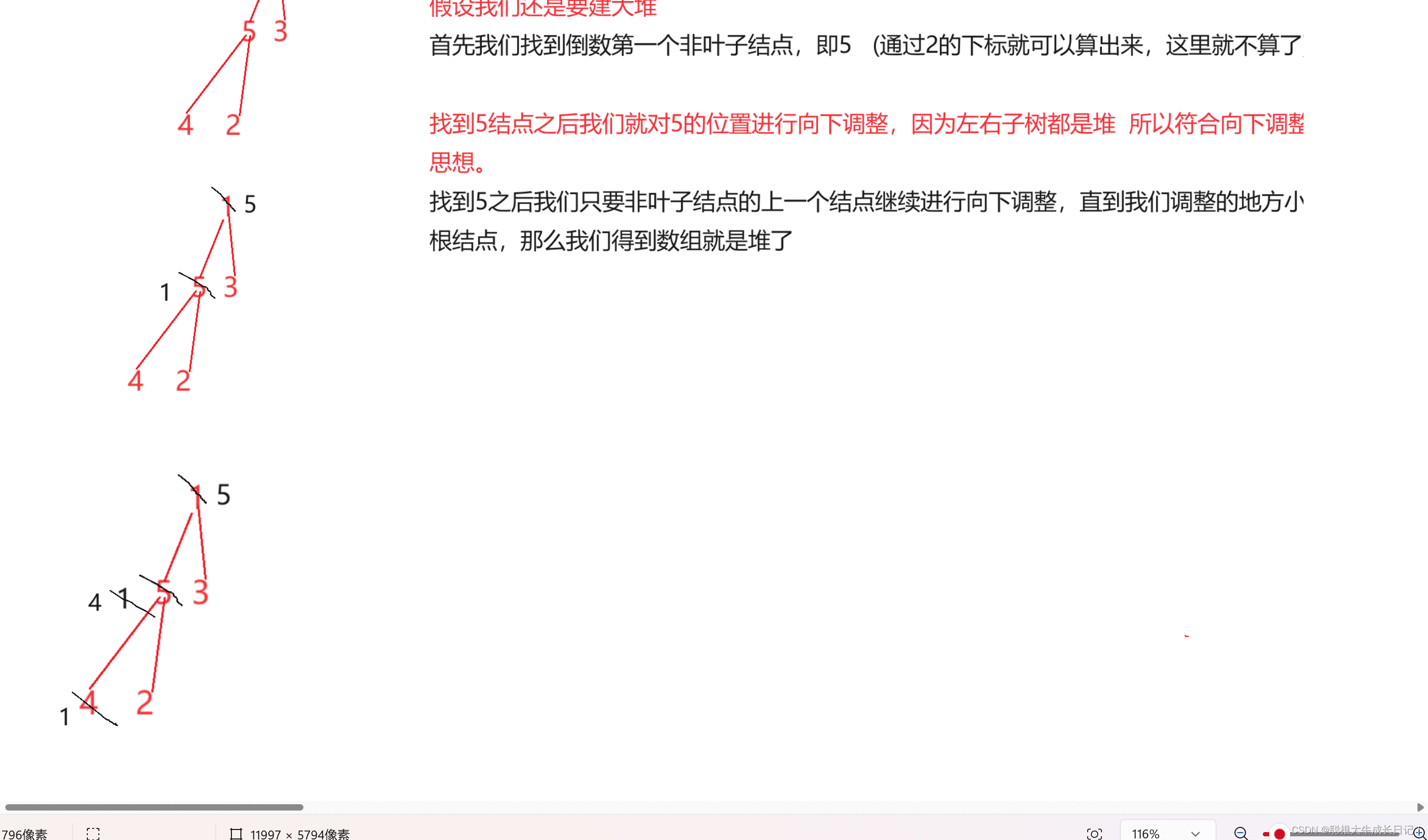
思路：找到倒数第一个非叶子结点，这样我们可以保证左右子树都是堆，才能够对整个堆使用向下调整算法的思想。

那么最后一个非叶子结点如何才能找到呢？这里不就是我们要记住的一个特点吗，通过孩子结点来算父亲结点。

parent=(child-1)/2;

我们先找到最后一个结点的下标，然后通过结点算父亲的公式不就可以算出来了吗

所以倒数第一个非叶子结点的下标不就是 (n-1-1)/2吗？

图解过程：

2:两种方法建堆复杂度的分析

首先我们直接公布结论：

向上调整算法的时间复杂度为O(N*logN),向下调整算法的时间复杂度为O(N),所以建堆在复杂度的层面来说向下调整算法是优于向上调整算法的。

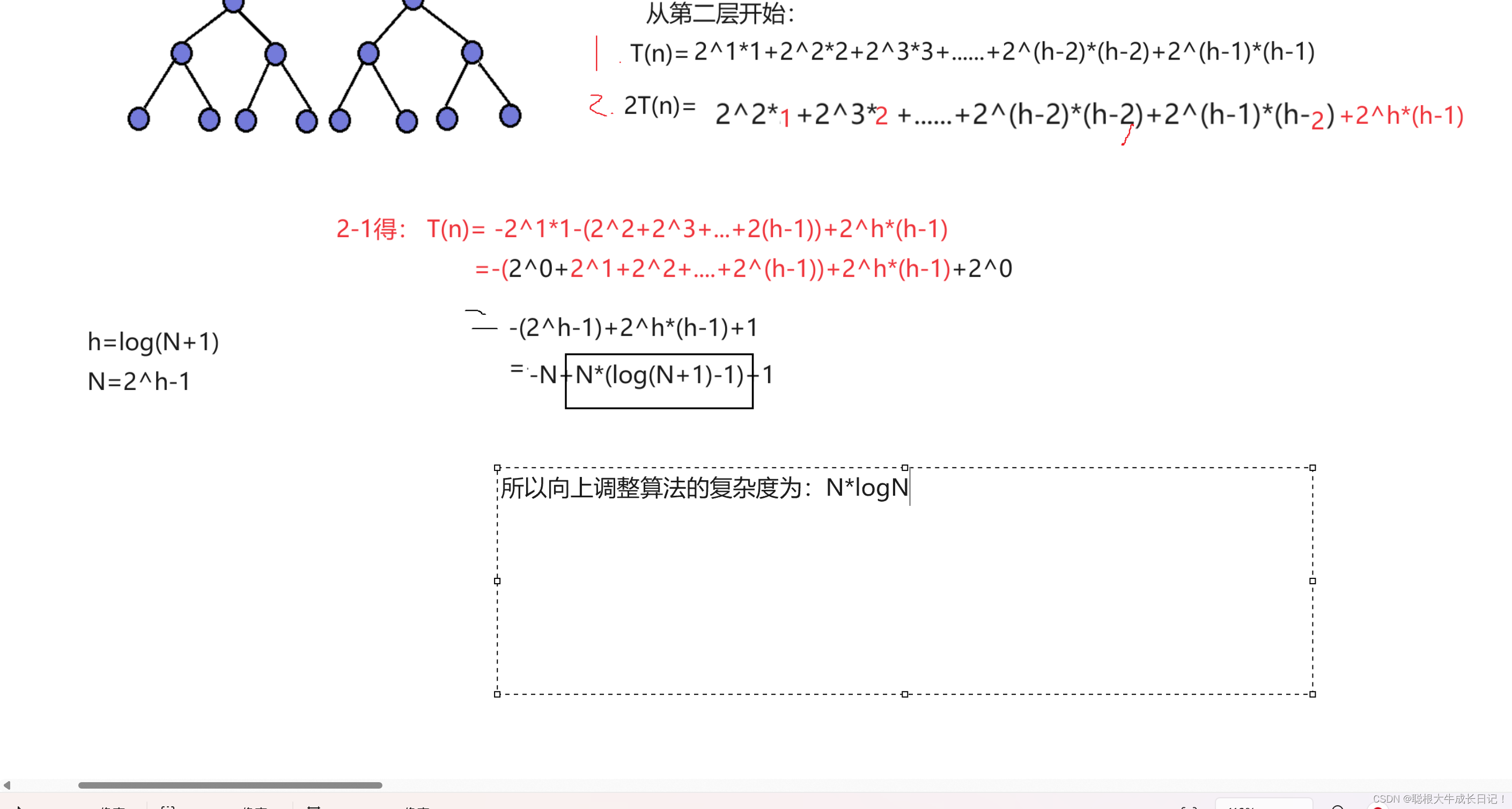
向上调整算法的时间复杂度分析：

我们知道向上调整算法是依次将后一个元素向上进行调整，那么最坏的情况下就是我们所插入一个数就要调整到根节点处。

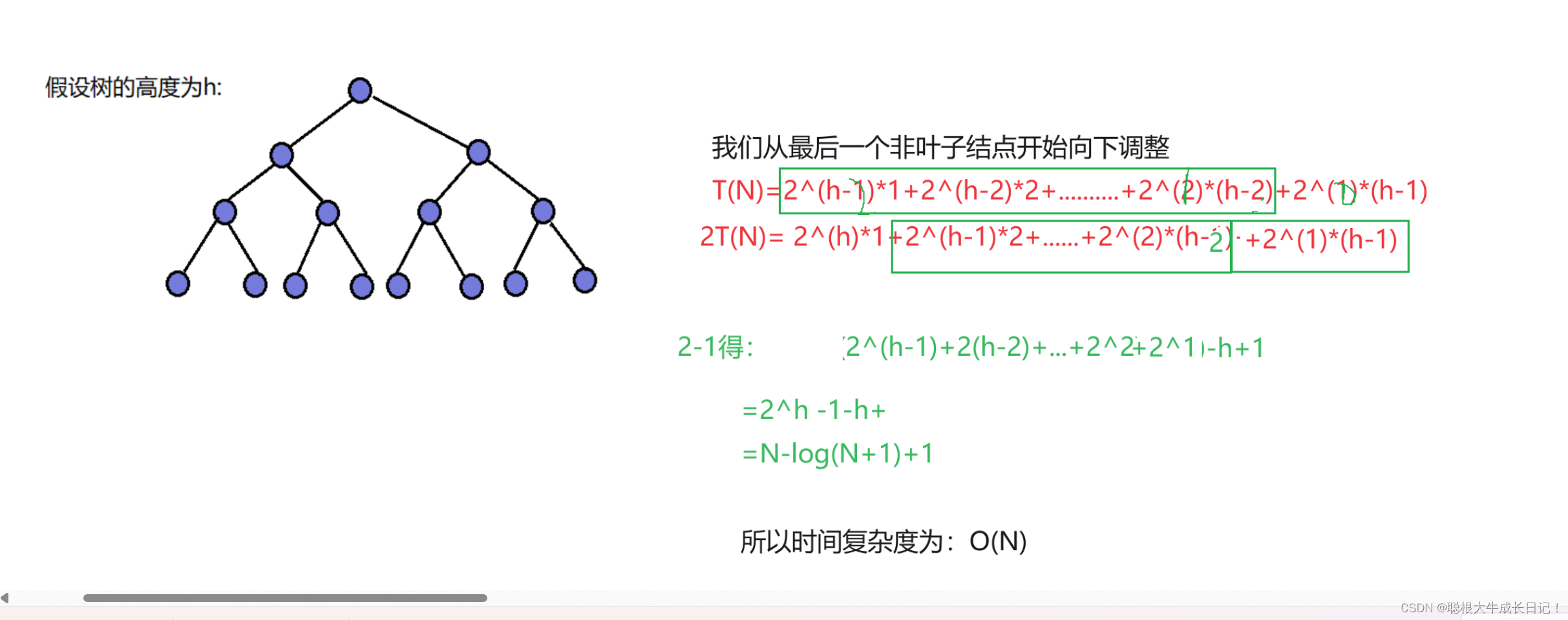
同理向下调整的复杂度分析

为啥同样都是建堆的过程，可是为啥向下调整算法的时间复杂度优于向上调整算法呢

因为向下调整算法时，最后一层结点不需要向下调整，且最后一层的结点比较多，从下往上，结点个数变少，乘以的层数变多，但是主要取决于时间复杂度的是结点个数多的。

而向上调整算法，最后一层结点的个数多，且需要调整的层数也最高，导致向上调整的时间复杂度高。

3.堆排序

在讲了前面两种算法的基础上我们就可以来谈一谈我们的堆排序了，堆排序并不是我们所讲的数据结构，虽然说堆数据结构也可以看出堆的升序与降序，但是我们可能并不是只要打印这个数组出来，我们可能还会进行一些算法，比如2分查找....。

堆排序的思路：

1：首先对数组进行建堆。

2：将最后一个元素与第一个元素交换，在向下进行调整

3：循环往复的进行，最后排除来的就是我们所需要的结果了。

那我们在排升序的时候应该见建大堆，还是小堆呢?

相信许多人在看到要排升序的时候，可能第一反应的是建小堆，因为小堆中的第一个数是所有元素中最小的那个数，但是当我们建立小堆的时候，那我们的第二个小的数字如何取呢？

且当我们将第一个元素排好之后，后面的元素的关系都不对了，就会形成兄弟变父子，父子叔侄变兄弟，那么我们可能还需要建一次堆，那么总体的时间复杂度为N*(N*logN),

所以我们排升序需要建大堆，排降序需要建小堆。

而我们为什么可以这样子做呢？

我们假设有一个数组我们已近将他建成大堆了，那么我们很明显知道根节点最大，那么我们就可以这样子做。

将最大的根结点与最后一个数字进行交换，由于我们只是交换了根结点与最后一个元素，其他的结构没有动，所以就可以使用向下调整，然后在对前n-1个元素进行向下调整，整个的时间复杂度为logn。每次选一个大的，我们向将大的排在最后，循环进行就可以排成我们所需要的结果了。

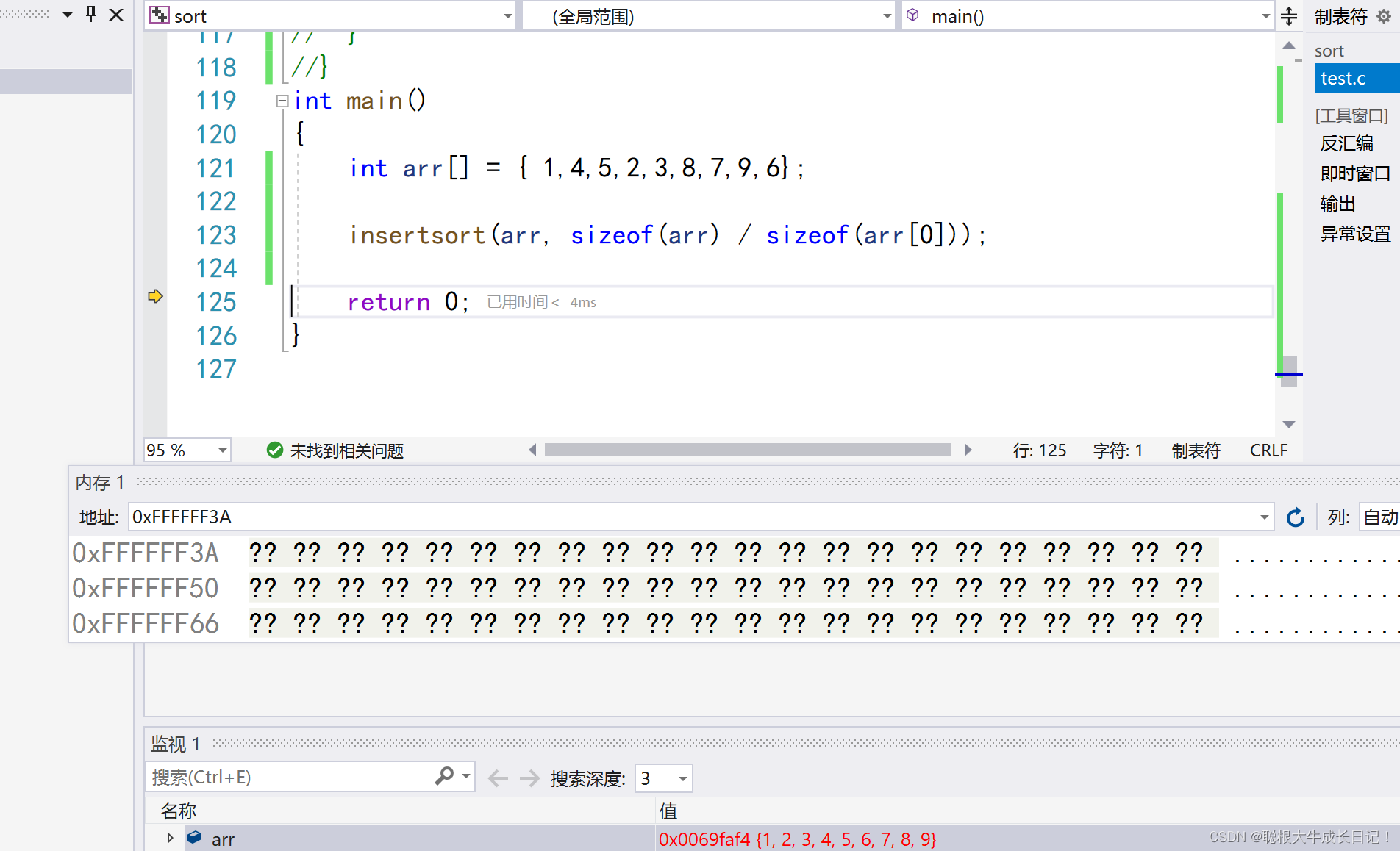
代码实现

void HeapSort(int* a, int n)
{
	//向下调整算法建堆,建大堆，排升序
	for (int i = (n-1-1)/2; i >=0; i--)
	{
		AdjustDown(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

也可以使用向上调整建堆进行堆排序：

假设排升序，建大堆
//void HeapSort(int* a, int n)
//{
//	//先建堆,用向上调整算法
//	for (int i = 1; i < n; i++)
//	{
//		AdjustUp(a, i);
//	}
//
//	//将最后一个数与根节点交换
//	//在进行向下调整，循环执行
//	int end = n - 1;
//	/*while (end > 0)
//	{
//		Swap(&a[end], &a[0]);
//		AdjustDown(a, end, 0);
//		--end;
//	}*/
//	
//	
//		
//
//}