数据结构——线性表之顺序表

news2024/11/23 7:24:15

目录

一.线性表

二.顺序表实现

 2.1 概念及结构

 2.2 动态顺序表

2.2.1 初始化与销毁函数

2.2.2 打印函数

2.2.3 尾插函数

2.2.4 尾删函数

2.2.5 扩容函数

2.2.6 头插函数

2.2.7 头删函数

2.2.8 任意位置插入函数

2.2.9 查找函数

2.2.10 任意位置删除函数 

2.2.11 修改函数

三.完整代码

四.力扣经典例题

3.1 移除元素

3.2 合并有序数组

五.结语

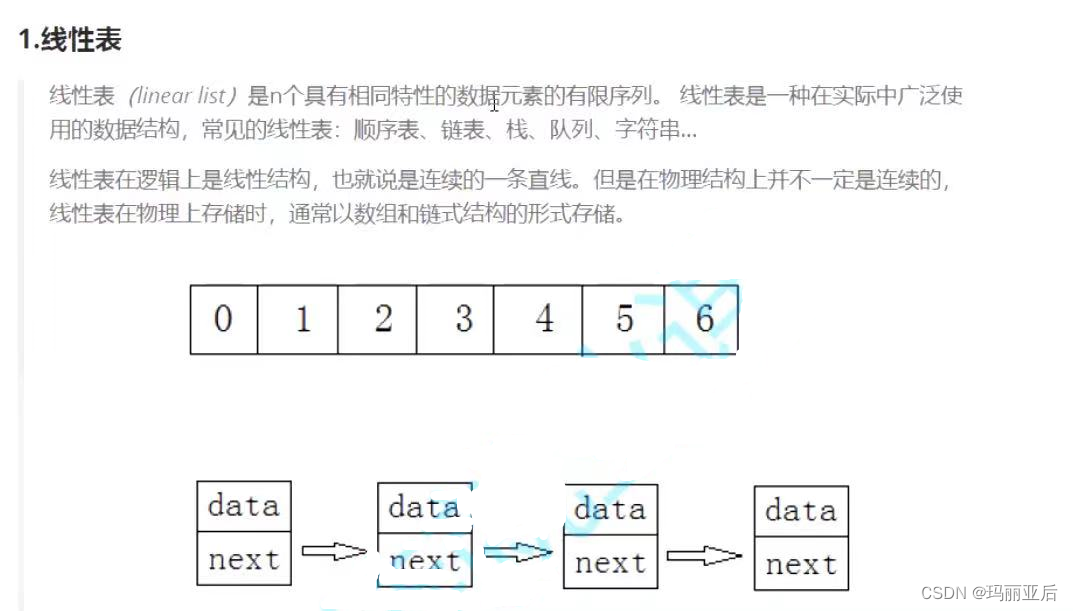
一.线性表

 二.顺序表实现

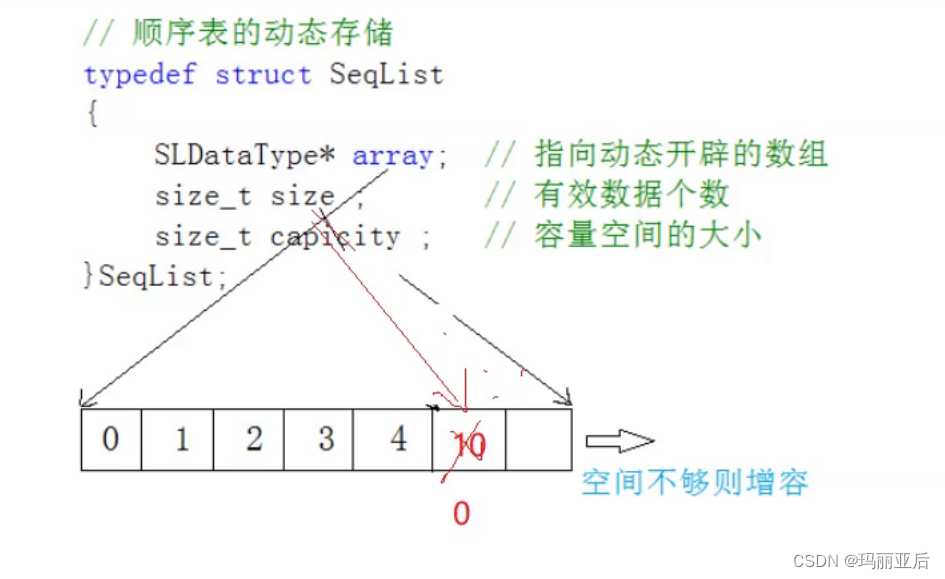
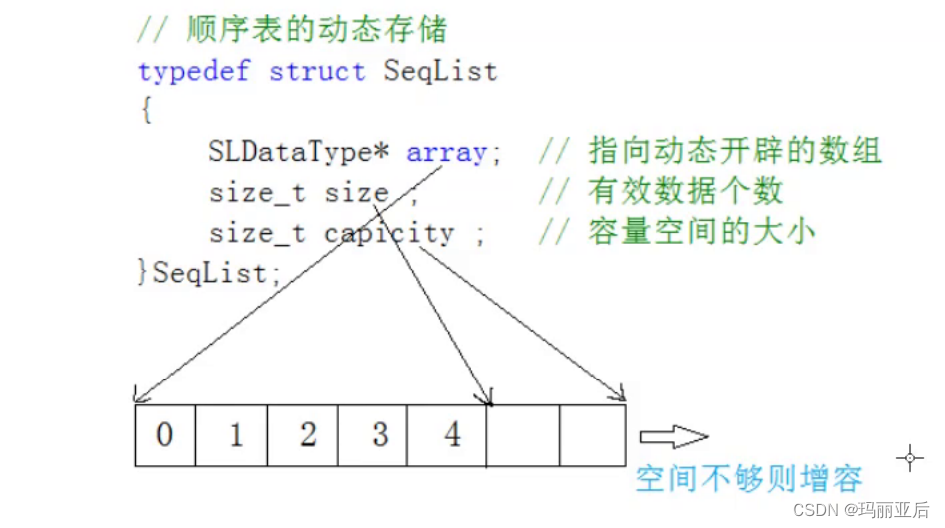
 2.1 概念及结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删查改。

顺序表一般可以分为：

  • 静态顺序表：使用定长数组存储（不好用）。
  • 动态顺序表：使用动态开辟的数组存储。

由于静态存储N定多了怕浪费，定少了又怕不够，我们简单提一嘴就好了，直接重点讲解动态顺序表。

 2.2 动态顺序表

先创造一个头文件和两个源文件 。

 

这里为了方便修改，引入了2个typedef。

2.2.1 初始化与销毁函数

再接一个初始化函数：

注意：这里的实参传输到形参的过程是传值调用，这样形参只是一份实参的临时拷贝，需要实参随形参改变的话那就得用到传址调用。

//SeqList.h
#pragma once
#include <stdio.h>
#include <string.h>

typedef int SLDataType;
struct SeqList
{
	SQDataType*a;
	
	int size;     //存储有效数据个数
    int capacity; //空间大小
};
//如果想方便输入可以这么定义：
typedef struct SeqList SL;
//这样两个单词就可以用SL来替代了
void SLInit(SL* ps);
​void SLDestr(SL* ps); //动态内存开辟时候不销毁可能会导致内存泄漏
//Test.c
#include "SeqList.h"
int main()
{
	SL sl;
	SLInit(&sl);

	return 0;
}

返回SeqList.c文件中定义初始化与销毁函数。 

//SeqList.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "SeqList.h"

void SLInit(SL* ps)
{
	ps->a = (SLDataType*)malloc(sizeof(SLDataType)*4);//虽然一开始可以让空间大小和malloc都置空，但这样不方便测试，所以先给空间。
	if (ps->a == 0)
	{
		perror("malloc failed");//验证malloc所创空间是否为空
		exit(-1);
	}
	ps->size = 0;
	ps->capacity = 4;

}
void SLDestr(SL* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->size = ps->capacity = 0;
}

接下来我们开始定义各种接口并实现其功能

//SeqList.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int SLDataType;
struct SeqList
{
	SLDataType* a;
	int size;
	int capacity;
};
typedef struct SeqList SL;

void SLInit(SL* ps);
void SLDestr(SL* ps);
//打印函数
void SLprint(SL* ps);
//扩容函数
void SLCheckCapacity(SL* ps);
//头插尾插，头删尾删
void SLPushBack(SL* ps, SLDataType x);
void SLPopBack(SL* ps);
void SLPushFront(SL* ps, SLDataType x);
void SLPopFront(SL* ps);

//顺序表在pos位置位置插入x
void SeqListInsert(SL* ps, size_t pos, SLDataType x);

//顺序表删除pos位置的值
void SeqListErase(SL* ps, size_t pos);
//查找函数
int SLFind(SL* ps, SLDataType x);
//修改函数
void SLModify(SL* ps, int pos, SLDataType x);

2.2.2 打印函数

//打印函数
void SLprint(SL* ps)
{
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->a[i]);
	}
	printf("\n");
}

2.2.3 尾插函数

关于realloc出来的空间不用free问题：

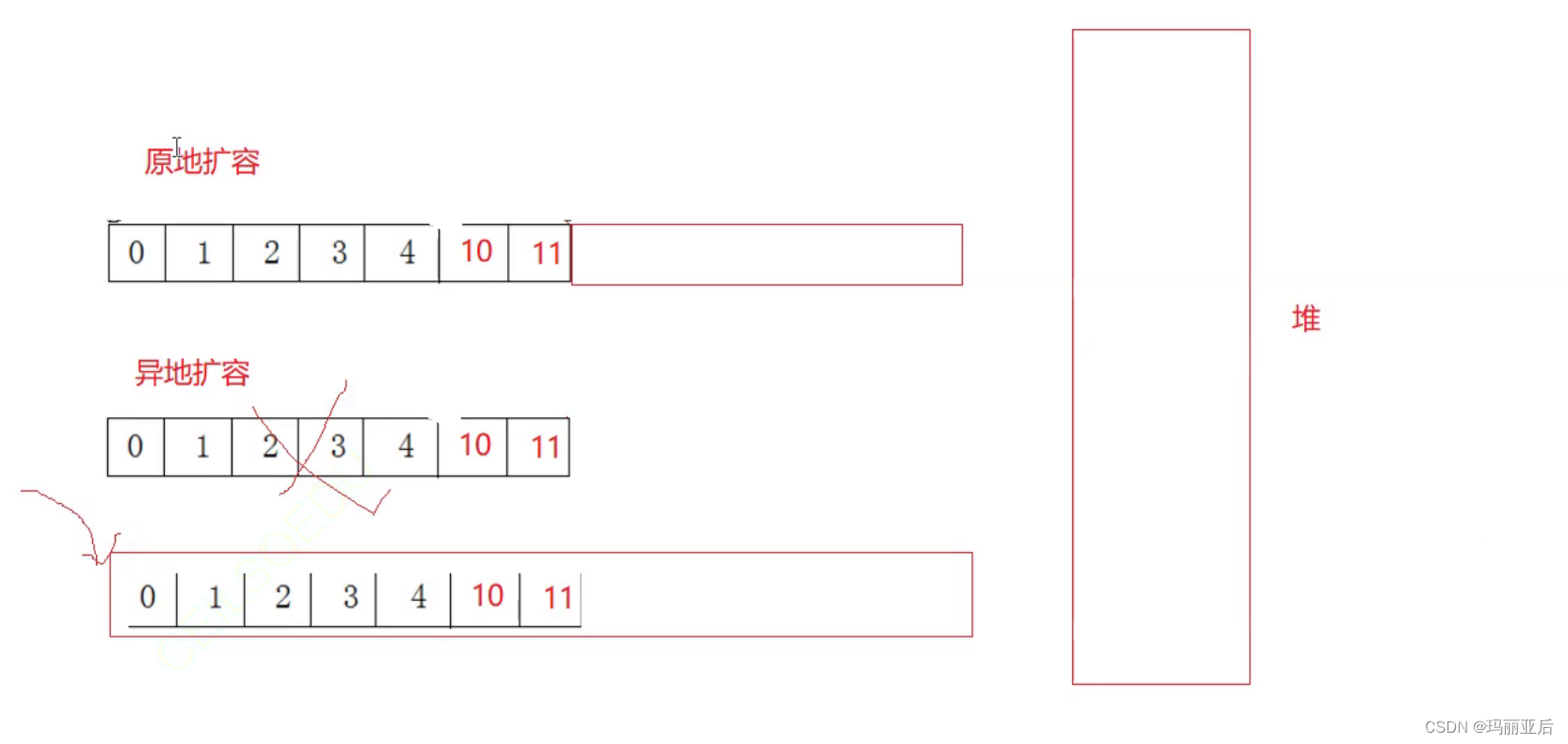
realloc分两种扩容(都有可能发生)，当要扩容时会分析后面是否有足够空间来分配给你，不够就会扩容。

第一种是原地扩容：即在原数组中再开辟多余的空间，这时候开辟过后的空间地址其实与原数组a是一致的。

第二种是异地扩容：即不在原空间，而是重新开辟出新的空间，新空间满足了扩容需求的同时还会把原数组中的元素拷贝过来。这时候原来的空间就会销毁。

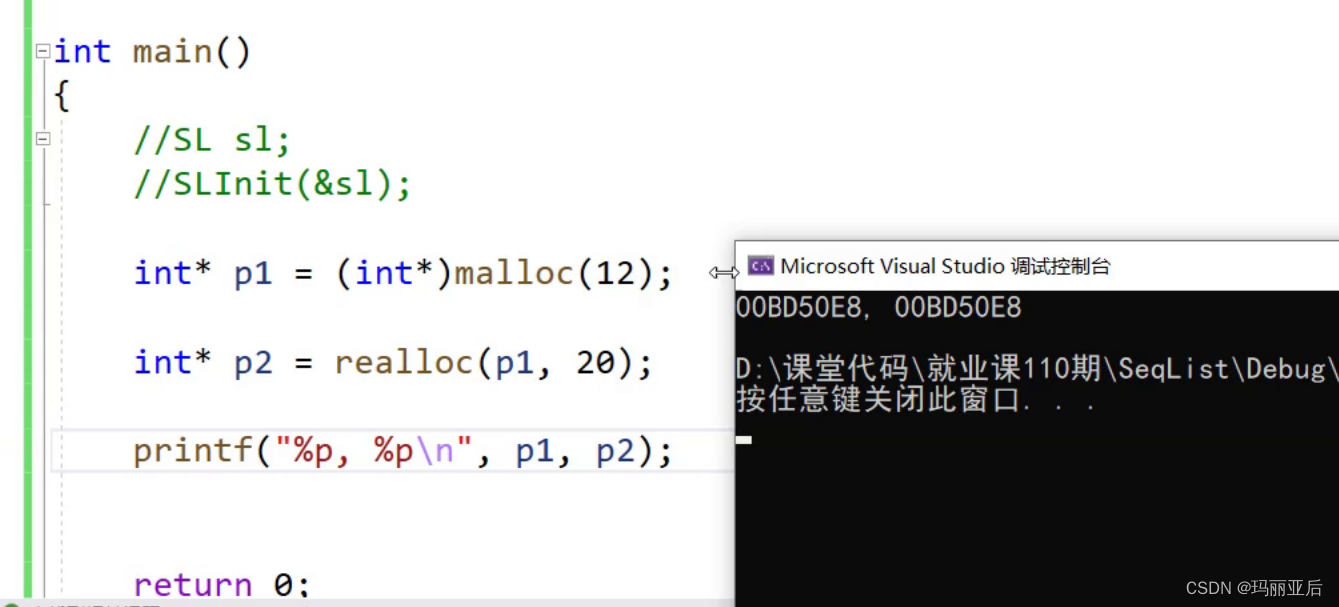
其实我们可以测试一下relloc会是哪种扩容：

 这种地址相同的就是原地扩容了

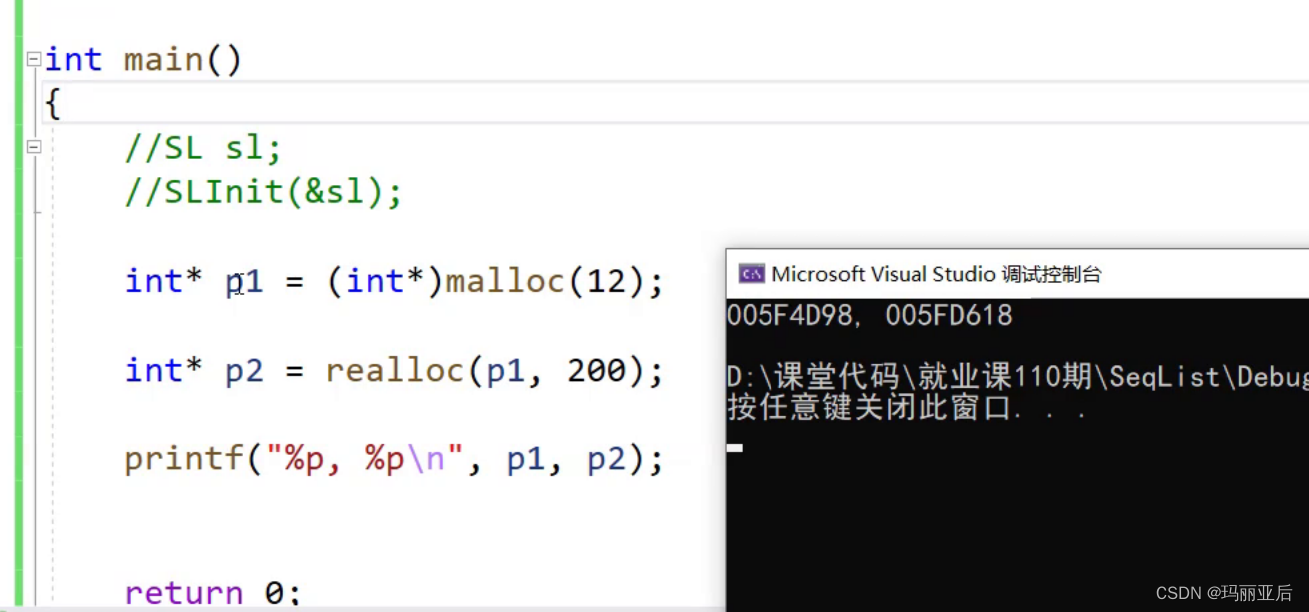
当我们设置大一点时就变成异地扩容了

因此解答了不用free的问题，因为realloc会自动帮你拷贝和释放。

//尾插函数
void SLPushBack(SL* ps, SLDataType x)
{
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 *(sizeof(SLDataType)));
		if (tmp == NULL)
		{
			perror("realloc failed");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity *= 2;
	}
	ps->a[ps->size] = x;
	ps->size++;


}

接下来我们来测试一下尾插并验证是否扩容：

//Test.c
#include <stdio.h>
#include "SeqList.h"
int main()
{
	SL sl;
	SLInit(&sl);
	/*int* p1 = (int*)malloc(12);
	int* p2 = realloc(p1, 10);
	printf("%p, %p\n", p1, p2);*/
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5);
	SLPushBack(&sl, 6);
	SLprint(&sl);
	SLDestr(&sl);

	return 0;
}

2.2.4 尾删函数

当我们让size--达到尾删时，是否需要把该处空间free掉？

答案是不行，因为malloc规定是整体创造空间并整体释放空间的，不能对整个空间中的一小处进行free，这是不被允许的。

如果尾删函数仅仅是这样写肯定是会出错的，当我们尾删多次直至让size减到了负数，那么后面就不能再进行插入了，因为size已经越界回不来了。 所以我们得规定让它不能越界。

​
void SLPopBack(SL* ps)
{
	//只要size指向不大于0，就不给继续尾删并且提示报错
	assert(ps->size > 0);
	ps->size--;
}

​

2.2.5 扩容函数

为了避免每一次的接口函数都要写上扩容标准，我们直接定义一个扩容函数来方便我们调用。

//扩容函数
void SLCheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));
		if (tmp == NULL)
		{
			perror("realloc failed");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity *= 2;
	}
}

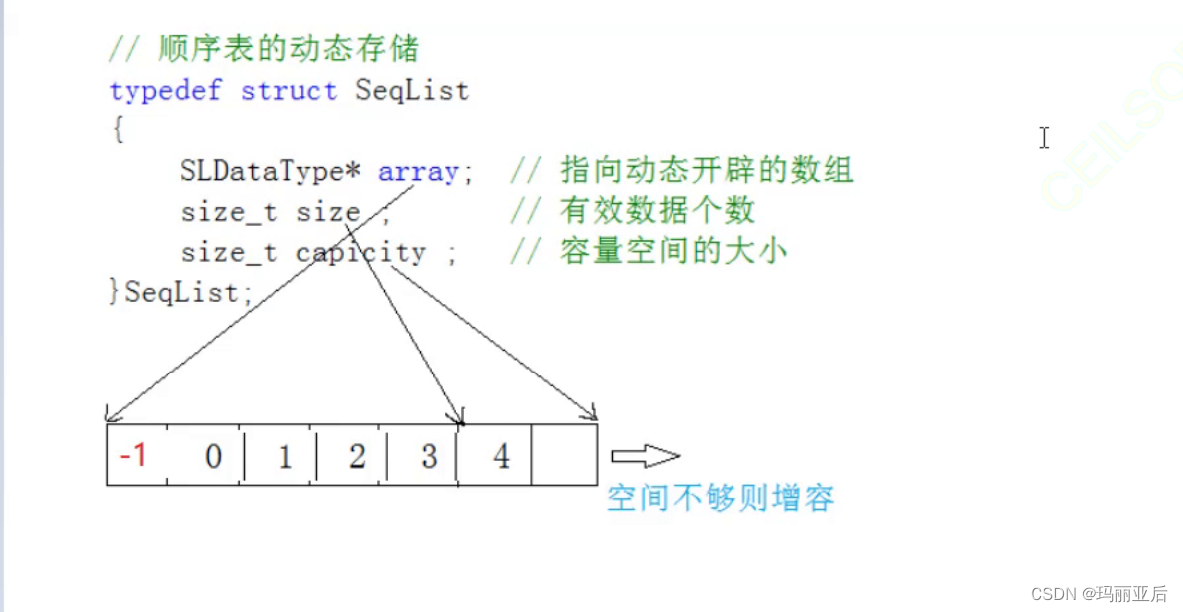
2.2.6 头插函数

基本思路是把空间里面原有的元素往后移动，记住是从最末尾的元素开始，如果从首元素开始移动，那么会覆盖掉后一个元素。


//头插函数
void SLPushFront(SL* ps, SLDataType x)
{
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
}

我们继续来测试一下

//测试函数
void TestSeqList2()
{
	SL sl;
	SLInit(&sl);
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5);
	SLPushBack(&sl, 6);
	SLPopBack(&sl);
	
	SLprint(&sl);

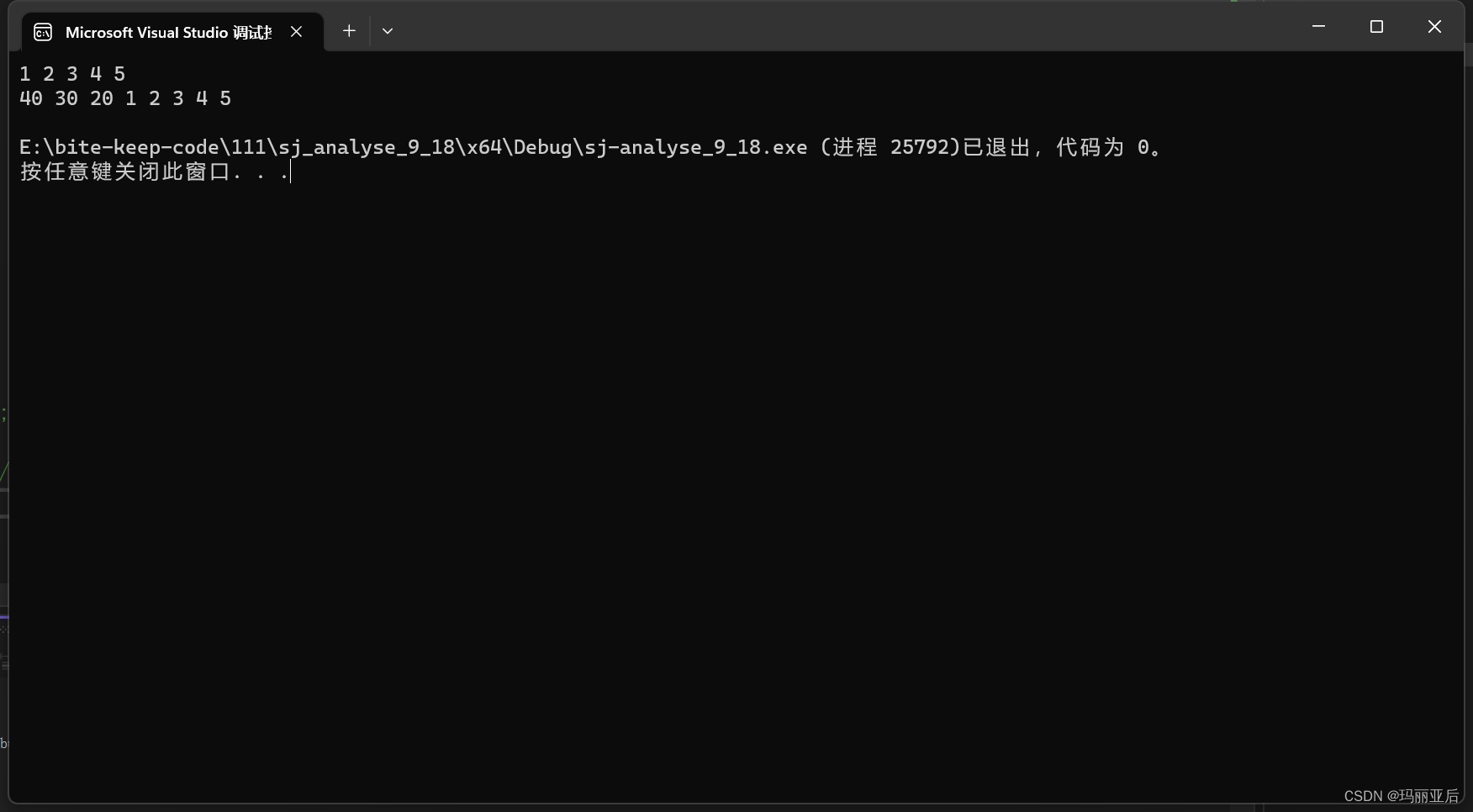
	SLPushFront(&sl, 20);
	SLPushFront(&sl, 30);
	SLPushFront(&sl, 40);
	SLprint(&sl);
	SLDestr(&sl);

}

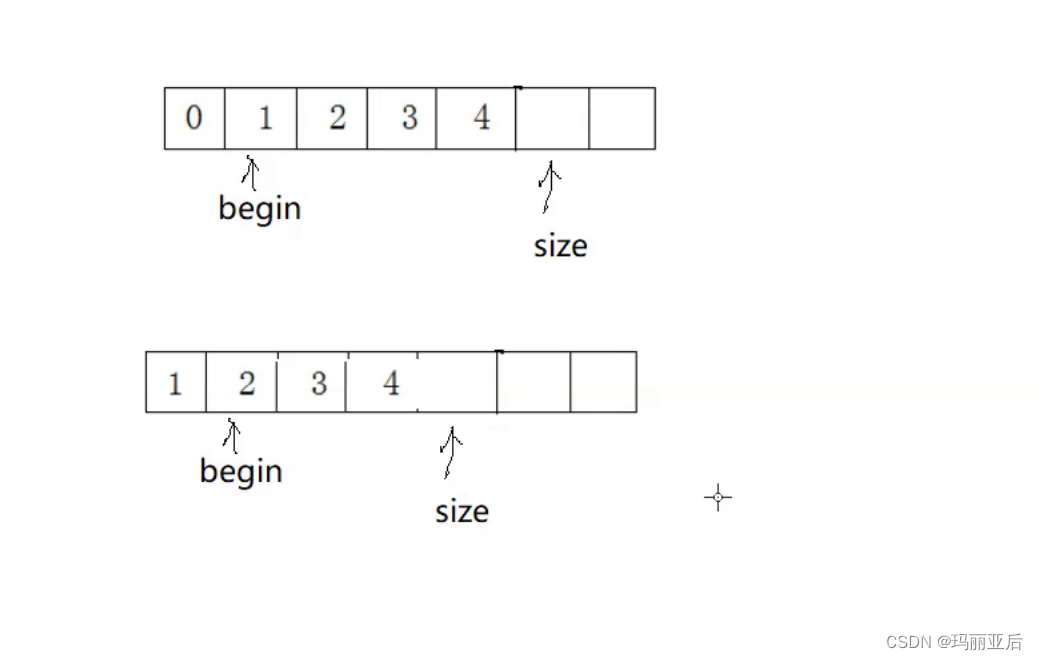
2.2.7 头删函数

在头删函数中我们则是要做到把后一位的元素往前一位覆盖的效果，别忘了最后再ps->size--

这段头删函数还是存在问题，如果size为0时，while不进入循环但size还是会--，这样又会造成之前的越界问题。所以要记得断言！

//头删函数
void SLPopFront(SL* ps)
{
	assert(ps->size > 0);
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;
	}
	ps->size--;

}

进行试验：先尾删3次，再头删一次

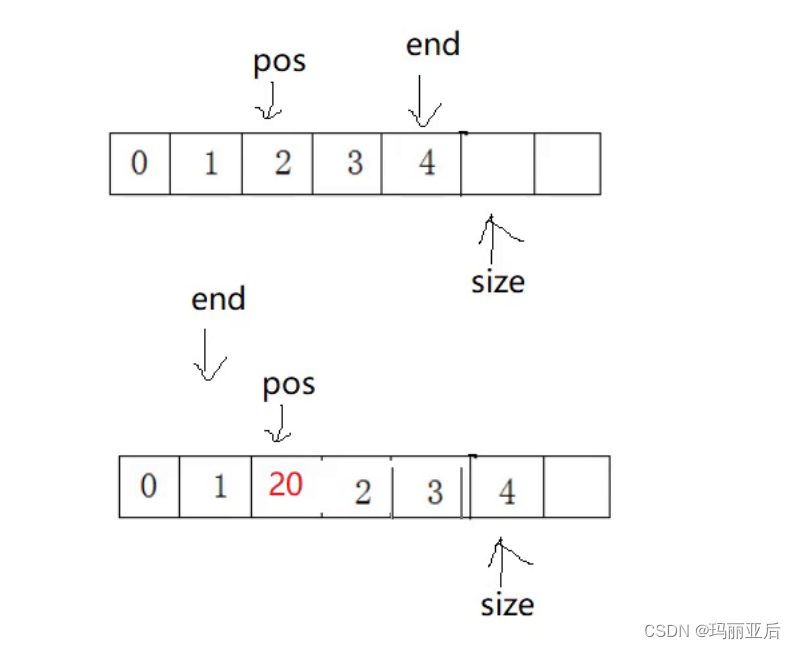
 2.2.8 任意位置插入函数

我们用断言来规定只能在数组元素范围内插入，接着再添加扩容函数。

既然要在某个位置中插入元素，那么它后面的元素就要往后移动，这里同样设置一个end，pos为我们想插入的下标。

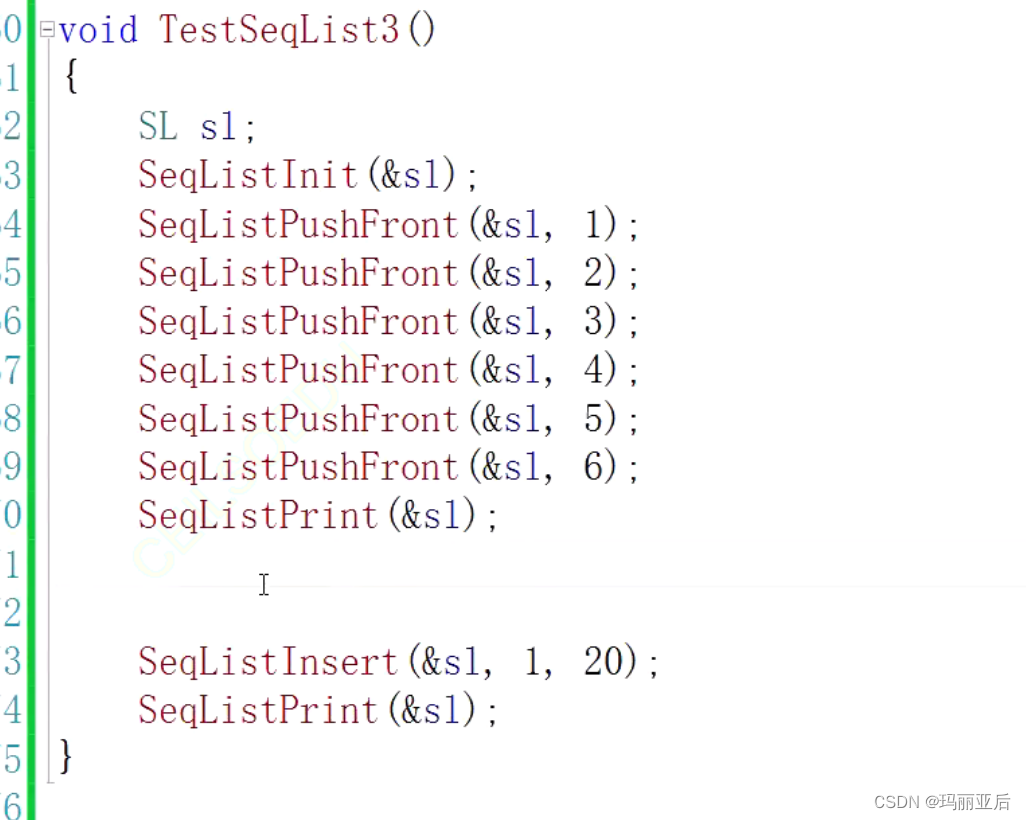
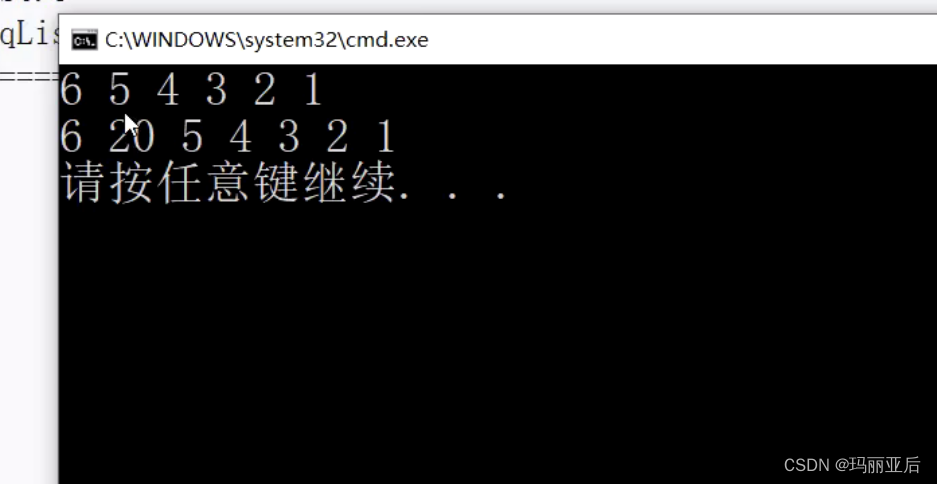
//顺序表在pos位置位置插入x
void SeqListInsert(SL* ps, size_t pos, SLDataType x)
{
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[pos] = x;
	ps->size++;


	
}

接下来进行试验：我们先头插6 5 4 3 2 1，再从下标为1的位置中插入20.

 

当我们完成Insert函数其实可以发现，它可以在头插和尾插函数里面进行复用。效果是一样的。

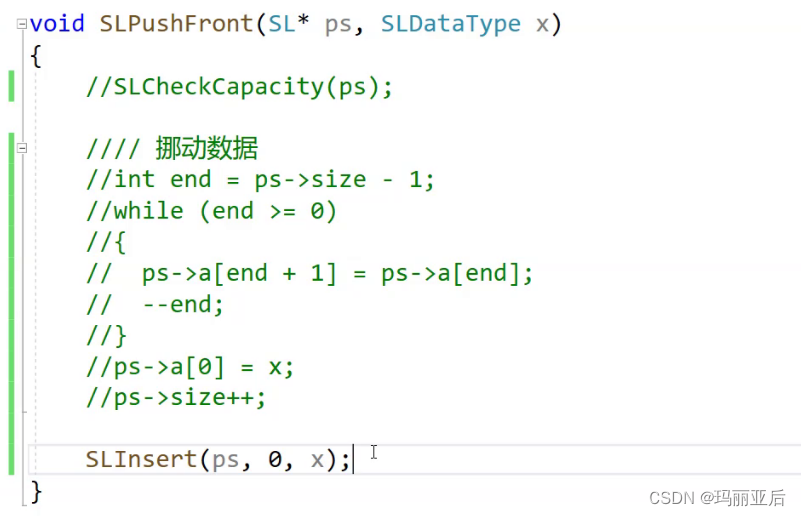
 2.2.9 查找函数

//查找函数
int SLFind(SL* ps, SLDataType x)
{
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}

	}
	return -1;
}

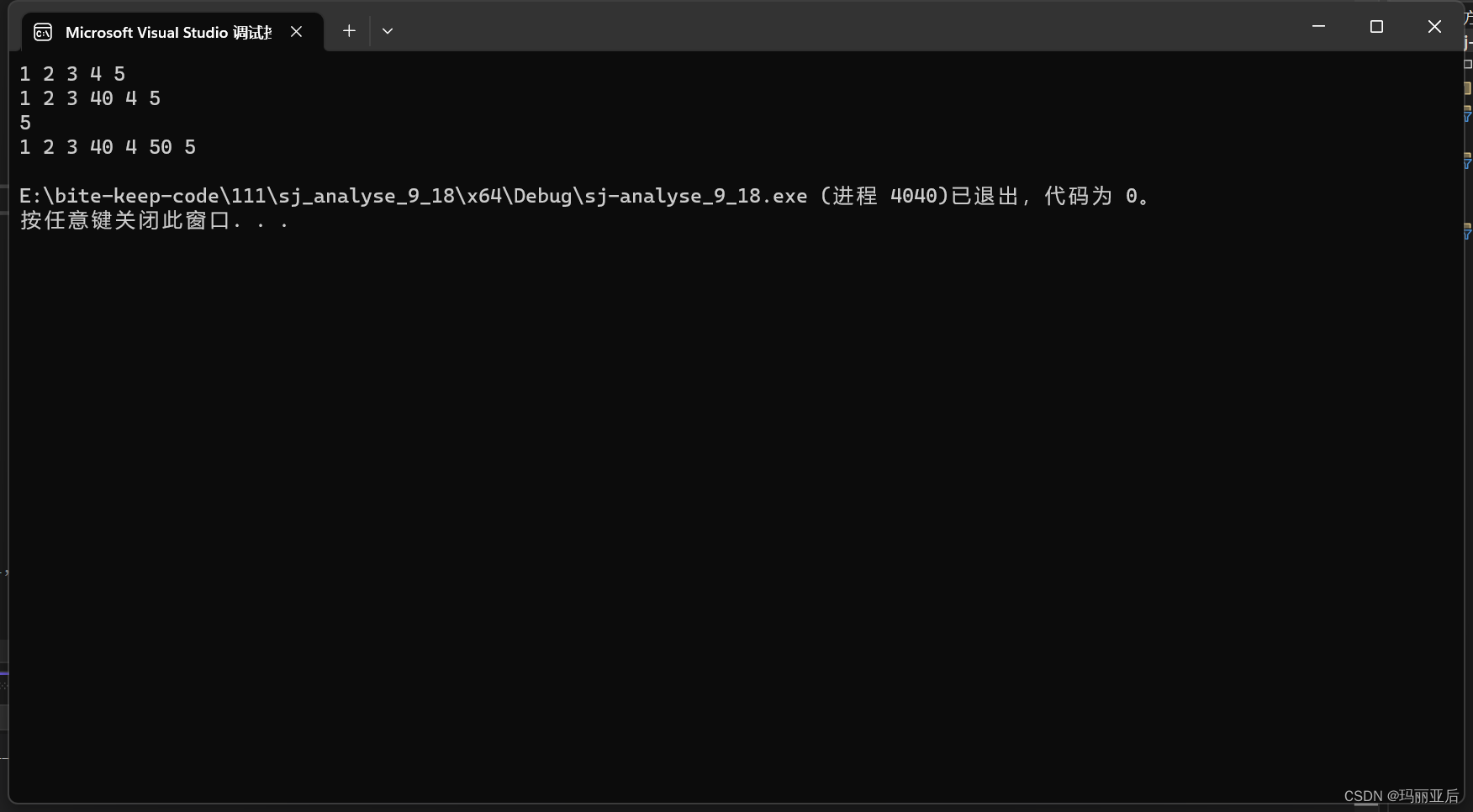
查找函数通常是跟其他接口函数搭配使用的，就比如与Insert搭配。

void TestSeqList3()
{
	SL sl;
	SLInit(&sl);
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5); 
	SLprint(&sl);

	SeqListInsert(&sl, 3, 40);
	SLprint(&sl);
	int x;
	scanf("%d", &x);
	int pos = SLFind(&sl, x);
	if (pos != -1)
	{
		SeqListInsert(&sl, pos, x * 10);
	}
	SLprint(&sl);
	SLDestr(&sl);

}

2.2.10 任意位置删除函数

老规矩，我们先断言pos只能在ps->size的范围内进行删除，当我们选定好要删除的下标时，需要把其后面的元素依次往前覆盖，这样就可以用覆盖来删除某一位置的元素了。

//顺序表删除pos位置的值
void SeqListErase(SL* ps, size_t pos)
{
	assert(pos >= 0 && pos < ps->size);//注意范围已经改变
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;
	}
	ps->size--;

}

进行试验：在任意位置插入函数实现的结果后我们再删除下标为1的元素

与Insert同理，Erase同样是可以复用的。

 2.2.11 修改函数

这里只需要注意断言使修改的位置在有效范围内就行了。

//修改函数

void SLModify(SL* ps, int pos, SLDataType x)
{
	assert(pos >= 0 && pos < ps->size);
	ps->a[pos] = x;
}

 至此增删查改结束了，我们可以编辑一个菜单来总结这些功能：

后面就慢慢用stitch语句慢慢完善就好了。 

 

三.完整代码

//SeqList.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int SLDataType;
struct SeqList
{
	SLDataType* a;
	int size;
	int capacity;
};
typedef struct SeqList SL;

void SLInit(SL* ps);
void SLDestr(SL* ps);
//打印函数
void SLprint(SL* ps);
//扩容函数
void SLCheckCapacity(SL* ps);
//头插尾插，头删尾删
void SLPushBack(SL* ps, SLDataType x);
void SLPopBack(SL* ps);
void SLPushFront(SL* ps, SLDataType x);
void SLPopFront(SL* ps);

//顺序表在pos位置位置插入x
void SeqListInsert(SL* ps, size_t pos, SLDataType x);

//顺序表删除pos位置的值
void SeqListErase(SL* ps, size_t pos);
//查找函数
int SLFind(SL* ps, SLDataType x);
//修改函数
void SLModify(SL* ps, int pos, SLDataType x);
//SeqList.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "SeqList.h"

void SLInit(SL* ps)
{
	ps->a = (SLDataType*)malloc(sizeof(SLDataType) * 4);//虽然一开始可以让空间大小和malloc都置空，但这样不方便测试，所以先给空间。
	if (ps->a == 0)
	{
		perror("malloc failed");//验证malloc所创空间是否为空
		exit(-1);
	}
	ps->size = 0;
	ps->capacity = 4;

}
void SLDestr(SL* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->size = ps->capacity = 0;
}

//打印函数
void SLprint(SL* ps)
{
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->a[i]);
	}
	printf("\n");
}

//扩容函数
void SLCheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2 * (sizeof(SLDataType)));
		if (tmp == NULL)
		{
			perror("realloc failed");
			exit(-1);
		}
		ps->a = tmp;
		ps->capacity *= 2;
	}
}

//尾插函数
void SLPushBack(SL* ps, SLDataType x)
{
	SLCheckCapacity(ps);
	ps->a[ps->size] = x;
	ps->size++;


}

//尾删函数
void SLPopBack(SL* ps)
{
	//只要size指向不大于0，就不给继续尾删并且提示报错
	assert(ps->size > 0);
	ps->size--;
}

//头插函数
void SLPushFront(SL* ps, SLDataType x)
{
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
}


//头删函数
void SLPopFront(SL* ps)
{
	assert(ps->size > 0);
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;
	}
	ps->size--;

}

//顺序表在pos位置位置插入x
void SeqListInsert(SL* ps, size_t pos, SLDataType x)
{
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[pos] = x;
	ps->size++;


	
}
//查找函数
int SLFind(SL* ps, SLDataType x)
{
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}

	}
	return -1;
}

//顺序表删除pos位置的值
void SeqListErase(SL* ps, size_t pos)
{
	assert(pos >= 0 && pos < ps->size);//注意范围已经改变
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;
	}
	ps->size--;

}
//修改函数

void SLModify(SL* ps, int pos, SLDataType x)
{
	assert(pos >= 0 && pos < ps->size);
	ps->a[pos] = x;
}
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
//Test.c
#include <stdio.h>
#include "SeqList.h"
void TestSeqList1()
{
	SL sl;
	SLInit(&sl);
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5);
	SLPushBack(&sl, 6);
	SLPopBack(&sl);
	SLprint(&sl);
	SLDestr(&sl);

}
void TestSeqList2()
{
	SL sl;
	SLInit(&sl);
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5);
	SLPushBack(&sl, 6);
	SLPopBack(&sl);
	
	SLprint(&sl);

	SLPushFront(&sl, 20);
	SLPushFront(&sl, 30);
	SLPushFront(&sl, 40);
	SLprint(&sl);
	SLDestr(&sl);

}

void TestSeqList3()
{
	SL sl;
	SLInit(&sl);
	SLPushBack(&sl, 1);
	SLPushBack(&sl, 2);
	SLPushBack(&sl, 3);
	SLPushBack(&sl, 4);
	SLPushBack(&sl, 5); 
	SLprint(&sl);

	SeqListInsert(&sl, 3, 40);
	SLprint(&sl);
	int x;
	scanf("%d", &x);
	int pos = SLFind(&sl, x);
	if (pos != -1)
	{
		SeqListInsert(&sl, pos, x * 10);
	}
	SLprint(&sl);
	SLDestr(&sl);

}


int main()
{
	/*SL sl;*/
	/*SLInit(&sl);*/
	/*int* p1 = (int*)malloc(12);
	int* p2 = realloc(p1, 10);
	printf("%p, %p\n", p1, p2);*/
	//TestSeqList1();
	//TestSeqList2();
	TestSeqList3();

	return 0;
}

四.力扣经典例题

3.1 移除元素

链接：力扣——移除元素

 

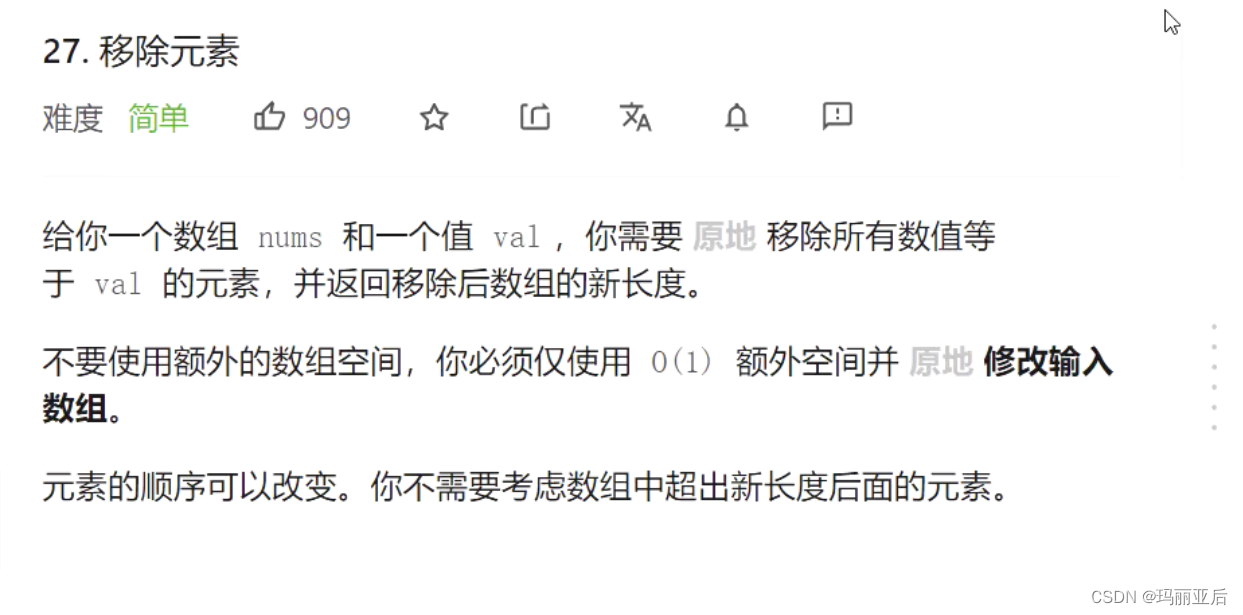
 一般我们的思路就是2.2.10任意位置删除元素的思想：

挨个遍历，如果指向的下标元素与val相同，那么把后面的元素依次覆盖，依次反复做到删除

 假设第一次排列移动了n次，那么第2次删除排列就是n-1次，等差数列求和一共执行了n^2次

 

 新数组拷贝回去后因为是malloc出来的，所以再把它释放掉就行了。空间复杂度为O（N）

这个想法核心是两个指针：一开始先让它们指向同一位置，用src来识别该值是否是val，如果不是就把这个值传到dst那里去，在同等指向时好像没什么不同，因为dst确实与src指向同一方向，然后二者共同向下一位进发。

转折点就是当src指向了第一个2（val的值）时，dst虽然也指向了2，但是dst不动，src向下一位进发，又指向了第二个2，dst还是不动，src继续进发指向了3.

最精彩的地方，因为src指向的3不是val（2）,所以src会把3传给dst，那么dst原本指向的第一个2就会被改变成3，以此类推我们会发现当src走完时，dst已经把2都给覆盖了。

 

另外我们也不用担心在str出去后原数组还有val要怎么办，因为问题是要求返回新数组的长度，所以dst的指向本身就可以代表新数组长度，所以不用管dst后面的元素。

int removeElement(int* nums, int numsSize, int val)
{
	int n = numsSize;
	int src = 0;
	int dst = 0;
	while (src < n)
	{
		if (nums[src] != val)
		{
			nums[dst] = nums[src];
			src++;
			dst++;
			
		}
		else if (nums[src] == val)
		{
			src++;
		}
	}
	return dst;
}

3.2 合并有序数组

链接：力扣——合并有序数组

 

这一道题也可以通过使用双指针的方法来进行合并有序数组：

首先，我们让两个指针都分别指向数组末尾的有效元素，然后同时进行比较。一开始a指向3，b指向6，6比3大，那么把b指向的6放入c中，同时b指向前一位的5，c也指向前一位的0.

a因为3比6小，所以还是指向a。

接着我们开始第二轮比较，指向3的a与指向5的b中，b更大所以重复操作b--,c在接受b传送的5后也跟着向前一位，c--。

现在a仍指向3，而b已经指向2了，3比2大，所以换成a把3传给c，然后二者都向前一位--。

至此，a向前一位指向2，b也指向2，而c指向的数值是3，让其中一位传给c即可，把3变成2，剩下的就不用处理了。

不过有一个问题：

当有负数的情况出现时，我们重复上述操作会发现nums1a的指向已经移出下标了没办法再排序了，而-2和-5却还没有排进去。

所以就需要当nums1数组已经结束时再添加一个条件，让没结束的nums2继续拷贝。

void merge(int* nums1, int sums1Size, int m, int* nums2, int sum2Size, int n)
{
	int end1 = m - 1;//第一个数组有效元素尾部
	int end2 = n - 1;//第二个数组有效元素尾部
	int end = m + n - 1;//第一个数组尾部
	while (end1 >= 0 && end2 >= 0)
	{
		if (nums1[end1] > nums2[end2])
		{
			nums1[end] = nums1[end1];
			end1--;
			end--;
		}
		else
		{
			nums1[end] = nums2[end2];
			end2--;
			end--;
		}
	}
	while (end2 >= 0)
	{
		nums1[end] = nums2[end2];
		end2--;
		end--;
	}
}

五.结语

我们可以发现做上述两道题和分析顺序表的时候最重要的思想就是学会画图，只要画图逻辑够清晰，那么代码是很容易写出来滴~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1022150.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2023年9月中国数据库排行榜：阿里叱咤云端登榜眼，华为中兴厚积薄发显峥嵘

2023年9月中国数据库排行榜：阿里叱咤云端登榜眼，华为中兴厚积薄发显峥嵘

鸿鹄展翅凌云志&#xff0c;骏马扬蹄踏雪心。 2023年9月的 墨天轮中国数据库流行度排行 火热出炉&#xff0c;本月共有287个数据库参与排名。本月排行榜前十中&#xff0c;OceanBase 连续10个月稳居榜首&#xff0c;头部产品得分差距日益缩小&#xff0c;阿里华为两大云厂商持续…
阅读更多...
react使用内联css样式的注意点

react使用内联css样式的注意点

react使用内联css样式: 就是直接在元素标签的style属性中写css样式&#xff0c;但是这里有三个注意点: 1. style等号后面必须接双大括号也就是 style{{ xx: xx }} 这样 2. css的属性必须写成驼峰型&#xff0c;不能有中横线&#xff0c;比如marginRight, 而不能说margin-righ…
阅读更多...
Axure原型设计累加器计时器设计效果（职业院校技能大赛物联网技术应用项目原型设计题目）

Axure原型设计累加器计时器设计效果（职业院校技能大赛物联网技术应用项目原型设计题目）

目录 前言 一、本题实现效果 二、操作步骤 1.新建文件 2.界面设计 2.1文本框 2.2 按钮 2.3设计界面完成 3.交互 3.1启动交互设置 3.2 分别设置三个属性 3.2.1 设置值为“0” 3.2.2 文字于文本框 3.2.3 获取焦点时 3.3 停止按钮的交互动作 3.3.1 设置变量值 3.4 重…
阅读更多...
CAC2023交流群（将持续更新至会议结束）

CAC2023交流群（将持续更新至会议结束）

为青年才俊们提供一个信息交换平台 看到大家对中国自动化大会非常感兴趣并踊跃投稿&#xff0c;虽然我和组委会没有什么直接联系&#xff0c;也是一个菜菜。只是把之前走过的坑写了出来&#xff0c;当然&#xff0c;这个会议你会投了&#xff0c;其它会议也是大同小异。 想必…
阅读更多...
java刷题知识点

java刷题知识点

文章目录 牛客网volatile字符串数组和字符数组管道解决hash冲突Java的体系结构包含下面有关servlet的层级结构和常用的类&#xff0c;说法正确的有?关于ThreadLocal类 以下说法正确的是off-heap是指那种内存集合和map的的继承实现关系抽象类和接口的区别节点流与处理流语句&am…
阅读更多...
Solidity 小白教程：21. 调用其他合约

Solidity 小白教程：21. 调用其他合约

Solidity 小白教程&#xff1a;21. 调用其他合约 调用已部署合约 开发者写智能合约来调用其他合约&#xff0c;这让以太坊网络上的程序可以复用&#xff0c;从而建立繁荣的生态。很多web3项目依赖于调用其他合约&#xff0c;比如收益农场&#xff08;yield farming&#xff0…
阅读更多...
SAP FI 中的重要报告

SAP FI 中的重要报告

目录 总账科目表 GL总账清单 GL总账余额 总账科目总计和余额 AR客户主数据列表 AR 客户余额 AR客户订单项 AR客户未清项目 AR客户付款记录 AR供应商主数据 AR供应商余额 AR供应商订单额 AR供应商未清项目 总账科目表 在 SAP 命令字段中输入交易代码 S_ALR_870123…
阅读更多...
数据分享|R语言生态学种群空间点格局分析：聚类泊松点过程对植物、蚂蚁巢穴分布数据可视化...

数据分享|R语言生态学种群空间点格局分析：聚类泊松点过程对植物、蚂蚁巢穴分布数据可视化...

全文链接 :https://tecdat.cn/?p33676 点模式分析&#xff08;点格局分析&#xff09;是一组用于分析空间点数据的技术。在生态学中&#xff0c;这种类型的分析可能在客户的几个情境下出现&#xff0c;但对数据生成方式做出了特定的假设&#xff0c;因此让我们首先看看哪些生态…
阅读更多...
中秋国庆假期——模板推荐

中秋国庆假期——模板推荐

要说最近能让人开心的事情是什么?大概就是下周将迎来8天假&#xff0c;小编帮大家数了数还有11天&#xff0c;就要放中秋国庆的假期了。作为一个资深打工人&#xff0c;本周的日常即将变成&#xff1a;上班想放假、下班想放假、想放假… 但是宝子们要注意&#xff0c;大家在盼…
阅读更多...
JDK8升级JDK11最全实践干货来了 | 京东云技术团队

JDK8升级JDK11最全实践干货来了 | 京东云技术团队

1、前言 截至目前&#xff08;2023年&#xff09;&#xff0c;Java8发布至今已有9年&#xff0c;2018年9月25日&#xff0c;Oracle发布了Java11&#xff0c;这是Java8之后的首个LTS版本。那么从JDK8到JDK11&#xff0c;到底带来了哪些特性呢&#xff1f;值得我们升级吗&#x…
阅读更多...
js中哪些地方会用到window？

js中哪些地方会用到window？

前言 Window 对象是JavaScript中的顶层对象&#xff0c;它代表了浏览器中打开的窗口或者标签页。浏览器中打开的每一个窗口/标签页都会有一个对应的 Window 对象。在浏览器中&#xff0c;全局作用域的 this 就是指向 Window 对象。 正文 在 JavaScript 中&#xff0c;window 对…
阅读更多...
《Python趣味工具》——自制emoji3

《Python趣味工具》——自制emoji3

今日目标 在上次&#xff0c;我们绘制了静态的emoji图。并且总结了turtle中的常用函数。 本次我们将尝试制作一个动态的emoji&#xff0c;让你的表情包动起来&#xff01; 文章目录 一、动画原理&#xff1a;二、制作动画&#xff1a;1. 修改eyes_black()函数&#xff1a;2. 绘…
阅读更多...
构建可维护的大规模应用：框架架构的最佳实践

构建可维护的大规模应用：框架架构的最佳实践

文章目录 框架架构的重要性最佳实践1. 模块化设计2. 遵循SOLID原则3. 使用设计模式4. 异常处理5. 代码注释和文档6. 测试 Spring Boot 和 Django&#xff1a;关键框架示例Spring Boot&#xff08;Java&#xff09;模块化设计&#xff1a;SOLID原则&#xff1a;设计模式&#xf…
阅读更多...
分类散点图 stripplot() 加辅助线axhline() 多图合一

分类散点图 stripplot() 加辅助线axhline() 多图合一

分类散点图 stripplot 加辅助线axhline 多图合一 效果图代码 画图没有什么可说的&#xff0c;直接上图 效果图 代码 # 绘制图&#xff0c; 查看是否数值在阈值上 plt.figure(figsize(30, 18)) n 0 for header, value_list in info_dict.items():ref_value_list ref_info_dic…
阅读更多...
three.js——通过顶点和顶点索引创建集合体

three.js——通过顶点和顶点索引创建集合体

通过顶点和顶点索引创建集合体 效果图1、创建顶点数据2、创建顶点属性3、创建材质4、创建网格5、改变网格的位置并添加到场景中6、通过顶点索引创建几何图形 效果图 1、创建顶点数据 // 创建顶点数据 每三个一个顶点 逆时针为正面 const vertices new Float32Array([ -1.0, -…
阅读更多...
uTool快捷指令

uTool快捷指令

send("************"); quickcommand.sleep(200); keyTap("enter");
阅读更多...
关于微信小程序rich-text中图片宽度超出范围解决办法

关于微信小程序rich-text中图片宽度超出范围解决办法

问题描述&#xff1a;写一个富文本展示页面时发现一个问题&#xff0c;就是图片宽度超出范围&#xff0c;本能反应是给图片设置一个最大宽度&#xff0c;这里发现不可行。然后又使用正则追加样式还是不行。 // 使用正则提取html里面的图片设置图片最大宽度为100% res[1].data[0…
阅读更多...
netty-HashedWheelTimer源码解析

netty-HashedWheelTimer源码解析

一、案例分析 public void testExecutionOnTaskExecutor() throws InterruptedException {int timeout 10;final CountDownLatch latch new CountDownLatch(1);final CountDownLatch timeoutLatch new CountDownLatch(1);Executor executor new Executor() {Overridepublic…
阅读更多...
用纯html写个个人简历！模版分享啦！！！

用纯html写个个人简历！模版分享啦！！！

用纯html写个个人简历&#xff01;首先得先找个模板&#xff01; 一个优秀模板所应该具有的素质&#xff1f; 简单&#xff1f; 仅仅一个html页面&#xff0c;完全没有乱七八糟&#xff0c;保证学的明明白白。 漂亮&#xff1f; 该有的内容一个不少&#xff01; 个人照片&a…
阅读更多...
零基础Linux_6(开发工具_下)函数库链接+Makefile+实现进度条+Git

零基础Linux_6(开发工具_下)函数库链接+Makefile+实现进度条+Git

目录 1. 函数库&#xff08;链接&#xff09; 1.1 链接 1.2 动态库与静态库 2. makefile 2.1 项目构建 2.2 Makefile的概念 2.3 Makefile的编写 2.4 .PHONY定义伪目标 ACM 时间 3.实现进度条&#xff08;缓冲区&#xff09; 3.1 缓冲区的概念 3.2 实现一个简易 &q…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023