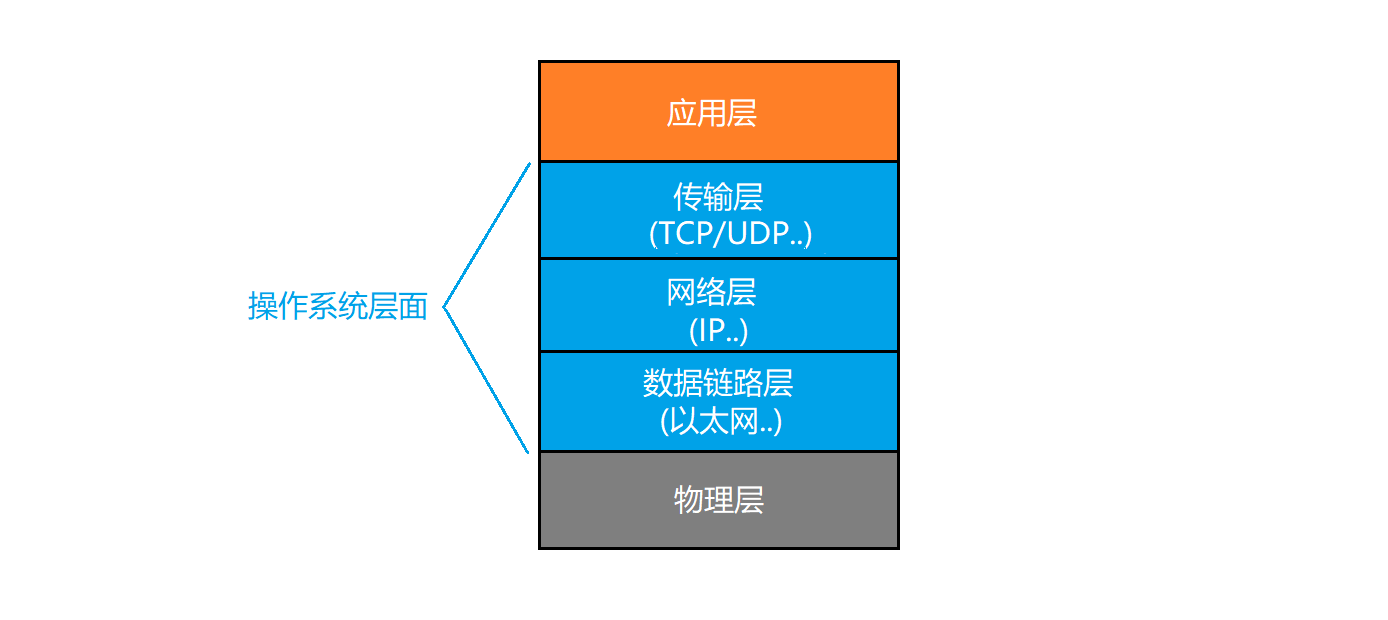
学习一下扩散模型的数学原理。
前向扩散
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right) q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)
其中, α t = 1 − β t \alpha_t = 1-\beta_t αt=1−βt
- 前向扩散过程没有可训练参数, β t \beta_t βt 是人工设置的超参
- x 0 x_0 x0 可以直接推导得到 x T x_T xT,而无须一步步迭代
逆向扩散
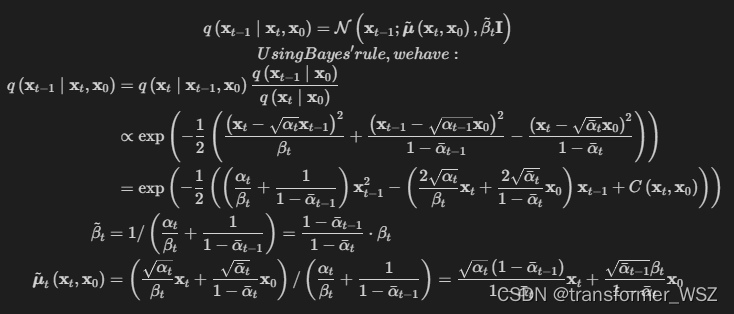
- 逆向扩散过程一步步去噪,需要训练参数
- x T x_T xT 不能一步推导到 x 0 x_0 x0,需要一步步迭代
损失函数
− log p θ ( x 0 ) ≤ − log p θ ( x 0 ) + D K L ( q ( x 1 : T ∣ x 0 ) ∥ p θ ( x 1 : T ∣ x 0 ) ) = − log p θ ( x 0 ) + E x 1 : T ∼ q ( x 1 : T ∣ x 0 ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 , T ) / p θ ( x 0 ) ] = − log p θ ( x 0 ) + E q [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) + log p θ ( x 0 ) ] = E q [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] Let L V L B = E q ( x 0 : T ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] ≥ − E q ( x 0 ) log p θ ( x 0 ) \begin{aligned} & -\log p_\theta\left(\mathbf{x}_0\right) \leq-\log p_\theta\left(\mathbf{x}_0\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right) \| p_\theta\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)\right) \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_{\mathbf{x}_{1: T \sim} q\left(\mathbf{x}_{\left.1: T \mid \mathbf{x}_0\right)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0, T}\right) / p_\theta\left(\mathbf{x}_0\right)}\right] \\ & =-\log p_\theta\left(\mathbf{x}_0\right)+\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}+\log p_\theta\left(\mathbf{x}_0\right)\right] \\ & =\mathbb{E}_q\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \\ & \text { Let } L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)}{p_\theta\left(\mathbf{x}_{0: T}\right)}\right] \geq-\mathbb{E}_{q\left(\mathbf{x}_0\right)} \log p_\theta\left(\mathbf{x}_0\right) \\ & \end{aligned} −logpθ(x0)≤−logpθ(x0)+DKL(q(x1:T∣x0)∥pθ(x1:T∣x0))=−logpθ(x0)+Ex1:T∼q(x1:T∣x0)[logpθ(x0,T)/pθ(x0)q(x1:T∣x0)]=−logpθ(x0)+Eq[logpθ(x0:T)q(x1:T∣x0)+logpθ(x0)]=Eq[logpθ(x0:T)q(x1:T∣x0)] Let LVLB=Eq(x0:T)[logpθ(x0:T)q(x1:T∣x0)]≥−Eq(x0)logpθ(x0)
最终化简得到的损失函数为:
L
simple
(
θ
)
:
=
E
t
,
x
0
,
ϵ
[
∥
ϵ
−
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
,
t
)
∥
2
]
L_{\text {simple }}(\theta):=\mathbb{E}_{t, \mathbf{x}_0, \epsilon}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right]
Lsimple (θ):=Et,x0,ϵ[
ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)
2]
确实非常简洁。。。
- 具体的推导可见:对数似然下界推导
模型训练与推理

FAQ
- 为什么建模目标不是直接预测原始输入 x 0 x_0 x0 ?
这个得看看原论文了。其实逆向扩散过程中模型预测的是噪音残差,跟ResNet思想一致。
- 前向可以 x 0 x_0 x0 可以直接推导得到 x T x_T xT,为什么后向不能 x T x_T xT 可以直接推导得到 x 0 x_0 x0?
其实是可以的,但一步到位直接预测 x 0 x_0 x0,但生成的图片效果较差。还是需要马尔科夫过程一步步生成高质量的图片。
参考
- The Illustrated Stable Diffusion
- 54、Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读
- 上述视频的置顶评论,是up主有关视频疑问的详细讲解
- 上述up主的代码实现