【图像压缩】余弦变换及霍夫曼编码jpeg压缩和解压【含Matlab源码 2086期】

⛄一、DCT图像无损压缩简介

1 图像压缩
图像压缩按照压缩过程中是否有信息的损失以及解压后与原始图像是否有误差可以分为无损压缩和有损压缩两大类。无损压缩是指不损失图像质量的压缩，它是对文件的存储方式进行优化，采用某种算法表示重复的数据信息，文件可以完全还原，不会影响文件内容。一般来说，由于无损压缩只是删除了图像数据中的冗余信息，可以准确地恢复原始图像，所以不可能达到很高的压缩比。有损压缩是指损失图像质量的压缩，它将不相干的信息也删除了，因此解压时只能将原始图像进行近似的还原，它的高压缩比是以牺牲图像质量为代价的。

2 JPRG图像压缩
JPEG 提出的 JPEG 标准是为连续色调图像的压缩提供的公共标准。连续色调图像并不局限于单色调( 黑白) 图像，该标准可适用于各种多媒体存储和通信应用所使用的灰度图像、摄影图像及静止视频压缩文件。
JPEG 标准还提出:
①必须将图像质量控制在可视保真度高的范围内，同时编码器可被参数化，允许设置压缩或质量水平
②压缩标准可以应用于任何一类连续色调数字图像，并不应受到维数、颜色、画面尺寸、内容和色调的限制
③压缩标准必须从完全无损到有损范围内可选，以适应不同的存储 CPU 和显示要求

图像压缩编码方法从压缩编码算法原理上可以分为无损压缩编码、有损压缩编码、混合编码方法。而JPEG 标准就是一种混合编码方法，既有无损的压缩编码又有有损的压缩编码。有损压缩方法是以 DCT 变换为基础的压缩方法，其压缩率比较高，是JPEG 标准的基础。无损压缩方法又称预测压缩方法，是以二维 DPCM 为基础的压缩方式，解码后能完全精确地恢复原图像采样值，其压缩比低于有损压缩方法。

观察下图中的编码器负责降低输入图像的编码、像素间和心理视觉冗余。在编码处理的第一阶段，离散余弦变换器将输入图像变换成一种( 通常不可见的) 格式，以便减少像素间的冗余。在第二阶段，量化器根据预定义的保真度准则来减少映射变换器输出的精确性，以便试图去除心理视觉冗余数据。这种操作是不可逆的，当进行无损压缩时，则必须将其忽略。在第三个即最后一个处理阶段，熵编码器根据所用的码字对量化器输出和离散余弦变换输出创建码字( 减少编码冗余）。
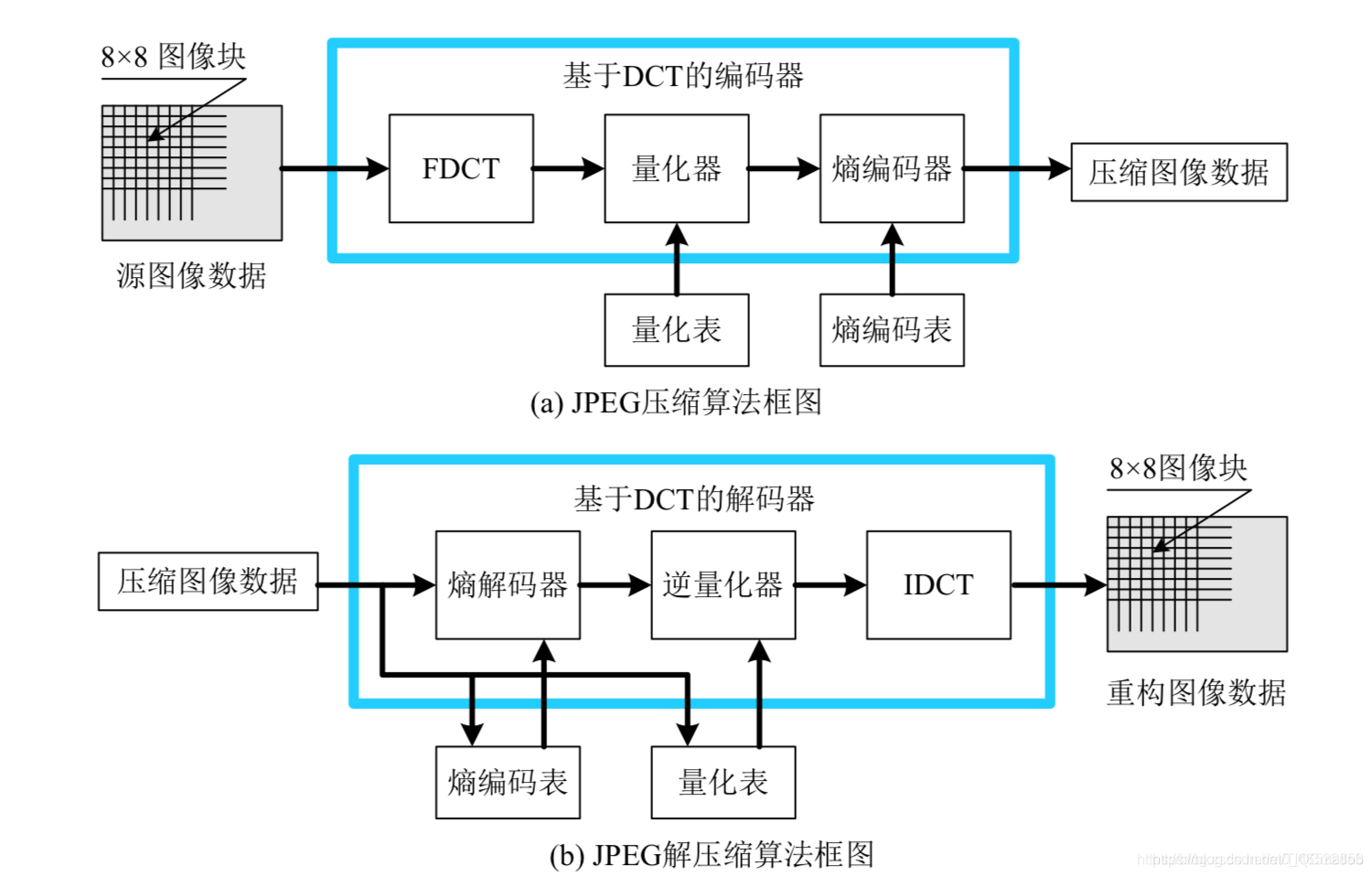
在这里插入图片描述
3 二维离散余弦变换
离散余弦变换(Discrete Cosine Transform),简称DCT变换.是一种与傅立叶变换紧密相关的数学运算.在傅立叶级数展开式中，如果被展开的函数是实偶函数，那么其傅立叶级数中只包含余弦项,再将其离散化可导出余弦变换，因此称之为离散余弦变换.余弦变换实际上是傅立叶变换的实数部分，其主要用于图像的压缩，目前国际压缩标准的JPEG格式中就用到了DCT变换。
在编码过程中,首先将输入图像颜色空间转换后分解为8× 8大小的数据块，然后用正向二维DCT把每个块转变成64个DCT系数值，其中1个数值是直流(DC)系数，即8× 8空域图像子块的平均值，其余的63个是交流(AC)系数，接下来对DCT系数进行量化，最后将变换得到的量化的DCT系数进行编码和传送，形成压缩后的图像格式。在解码过程中,先对已编码的量化的DCT系数进行解码，然后使用二维DCT反变换求逆量化并把DCT系数转化为8× 8样本像块，最后将操作完成后的块组合成一个单一的图像。这样就完成了图像的压缩和解压过程.研究表明，DCT将8× 8图像块变换为频域时数值集中在左上角，即低频分量都集中在左上角，高频分量分布在右下脚。而低频部分包含了图像大部分信息，相比之下，高频部分包含的信息量较少。为了压缩数据，往往采用忽略高频系数的办法。而较低频系数的修改对原始数据的影响较小。基于DCT的压缩编码属于有损压缩，通过去除图像本身的冗余量和人的视觉冗余量来达到压缩数据的目的，主要分为以下几个步骤:
(1)正向离散余弦变换
(2)量化
(3)Z字形编码
(4)使用差分脉冲编码调制对直流系数进行编码
(5)使用行程长度编码对交流系数进行编码
(6)熵编码
(7)组成位数据流

4 二维DCT变换
二维离散余弦变换的正变换公式为:
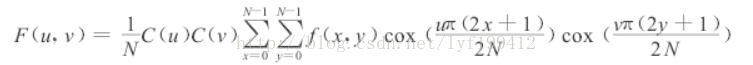
在这里插入图片描述
在图像的压缩编码中,N一般取8。
二维DCT的反变换公式为:

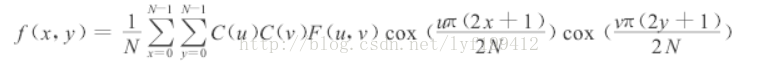
以上各式中的系数:

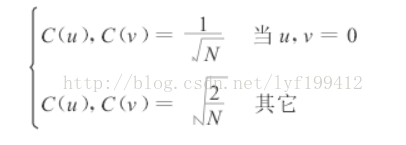
5 Matlab调试
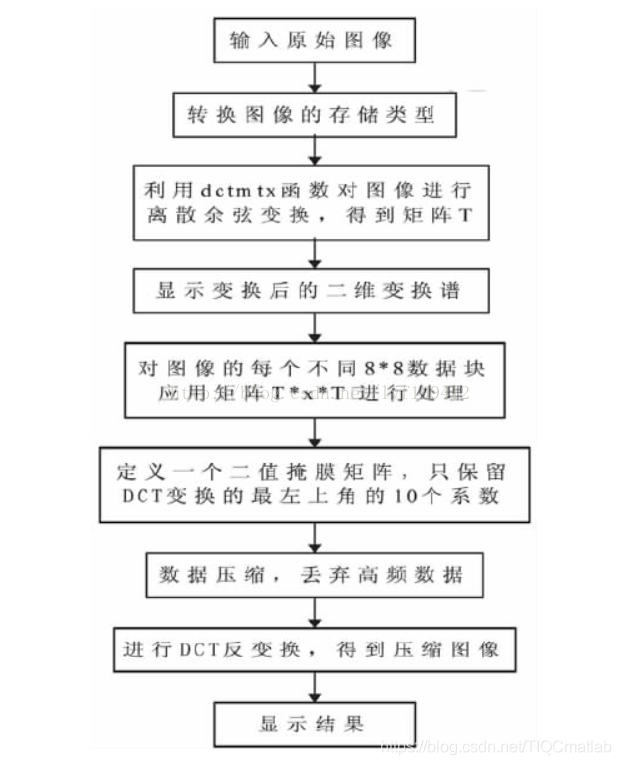
根据JPEG 压缩编码算法，要将一幅灰度图像进行压缩编码，首先把图像分成 8* 8 的像素块，分块进行 DCT 变换后，根据 JPEG 标准量化表对变换系数进行量化，再对直流系数( DC) 进行预测编码，对交流系数( AC) 行 zigzag 扫描和可变长编码，然后根据标准的 Huffman 码表进行熵编码，输出压缩图像的比特序列，实现了图像的压缩。
DCT 变换的特点是变换后图像大部分能量集中在左上角，因为左上角反应原图像低频部分数据，右下角反应原图像高频部分数据，而图像的能量通常集中在低频部分。因此 DCT 变换后，只保留 DCT 系数矩阵最左上角的 10 个系数，然后对每个图像块利用这 10个系数进行 DCT 反变换来重构图像。
其基于 DCT 变换矩阵算法的处理过程如下图：
在这里插入图片描述

⛄二、部分源代码

close all;
clear all;

% Read the original images to the matrix orig_image;
clear orig_image;
clear temp_image;
temp_image = imread(‘image1.bmp’);
orig_image(:,:,:,1) = double(temp_image(:,:,:,1));
clear temp_image;
temp_image = imread(‘image2.bmp’);
orig_image(:,:,:,2) = double(temp_image(:,:,:,1));
clear temp_image;
temp_image = imread(‘image3.bmp’);
orig_image(:,:,:,3) = double(temp_image(:,:,:,1));
clear temp_image;
temp_image = imread(‘image4.bmp’);
orig_image(:,:,:,4) = double(temp_image(:,:,:,1));

% Image compression
% You are required to implement this part
% Note: The components of comp_image should be integers
starttime = cputime;
clear comp_image;
[comp_image_Y1,comp_image_U1,comp_image_V1] = Compress(orig_image(:,:,:,1));
[comp_image_Y2,comp_image_U2,comp_image_V2] = Compress(orig_image(:,:,:,2));
[comp_image_Y3,comp_image_U3,comp_image_V3] = Compress(orig_image(:,:,:,3));
[comp_image_Y4,comp_image_U4,comp_image_V4] = Compress(orig_image(:,:,:,4));
comp_size = comp_image_Y1.realsize+comp_image_U1.realsize+comp_image_V1.realsize;
%comp_image = zeros(comp_image_Y1.realsize,comp_image_U1.realsize,comp_image_V1.realsize);
% Image decompression
% You are required to implement this part
% Note: The components of reco_image shoud be integers
% The size of the reco_image should be same with the orig_image
clear reco_image;
s_image1 = Decompress(comp_image_Y1,comp_image_U1,comp_image_V1);
s_image2 = Decompress(comp_image_Y2,comp_image_U2,comp_image_V2);
s_image3 = Decompress(comp_image_Y3,comp_image_U3,comp_image_V3);
s_image4 = Decompress(comp_image_Y4,comp_image_U4,comp_image_V4);
%figure,imshow(s_image),title(‘jjiayatuxl’);
reco_image(:,:,:,1) = double(s_image1(:,:,:,1));
reco_image(:,:,:,2) = double(s_image2(:,:,:,1));
reco_image(:,:,:,3) = double(s_image3(:,:,:,1));
reco_image(:,:,:,4) = double(s_image4(:,:,:,1));
runtime = cputime - starttime;

% Check the size of the recovered image
clear sizevector1;
clear sizevector2;
[m1,m2,m3] = size(orig_image);
sizevector1 = size(orig_image);
sizevector2 = size(reco_image);
if sizevector1==sizevector2

% Calculate the compression ratio
%comp_image = double(comp_image);
%comp_ratio = Compratio(orig_image, round(comp_image));
comp_ratio = m1*m2*m3/comp_size;
% Calculate the distortion of the recovered images using Mean Square Error
reco_image = double(reco_image);
MSE = CalMSE(orig_image, round(reco_image));
% Display the original image and recovered image
figure(1);
subplot(2,2,1);
clear disp_image;
disp_image = orig_image(:,:,:,1);
imdisplay(disp_image);
title('Original Image 1');
subplot(2,2,2);
clear disp_image;
disp_image = reco_image(:,:,:,1);
imdisplay(disp_image);
title('Recovered Image 1');
subplot(2,2,3);
clear disp_image;
disp_image = orig_image(:,:,:,2);
imdisplay(disp_image);
title('Original Image 2');
subplot(2,2,4);
clear disp_image;
disp_image = reco_image(:,:,:,2);
imdisplay(disp_image);
title('Recovered Image 2');

figure(2);
subplot(2,2,1);
clear disp_image;
disp_image = orig_image(:,:,:,3);
imdisplay(disp_image);
title('Original Image 3');
subplot(2,2,2);
clear disp_image;
disp_image = reco_image(:,:,:,3);
imdisplay(disp_image);
title('Recovered Image 3');
subplot(2,2,3);
clear disp_image;
disp_image = orig_image(:,:,:,4);
imdisplay(disp_image);
title('Original Image 4');
subplot(2,2,4);
clear disp_image;
disp_image = reco_image(:,:,:,4);
imdisplay(disp_image);
title('Recovered Image 4');
  
% Output the performance
ratiomesg = sprintf('The compression ratio is = %6.2f\n', comp_ratio);
disp(ratiomesg );
distortionmesg = sprintf('The MSE is = %6.2f\n', MSE);
disp(distortionmesg );
timemesg = sprintf('The running time is = %6.2f\n', runtime);
disp(timemesg );

else
disp(‘The size of the recovered image is not correct’);
end