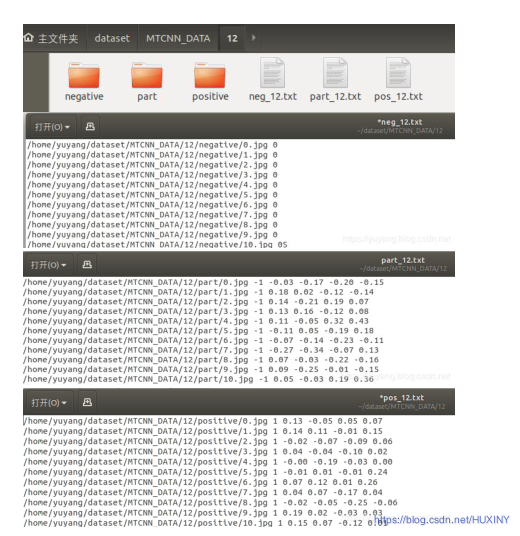
337. 打家劫舍 III - 力扣(LeetCode)
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
示例 1:

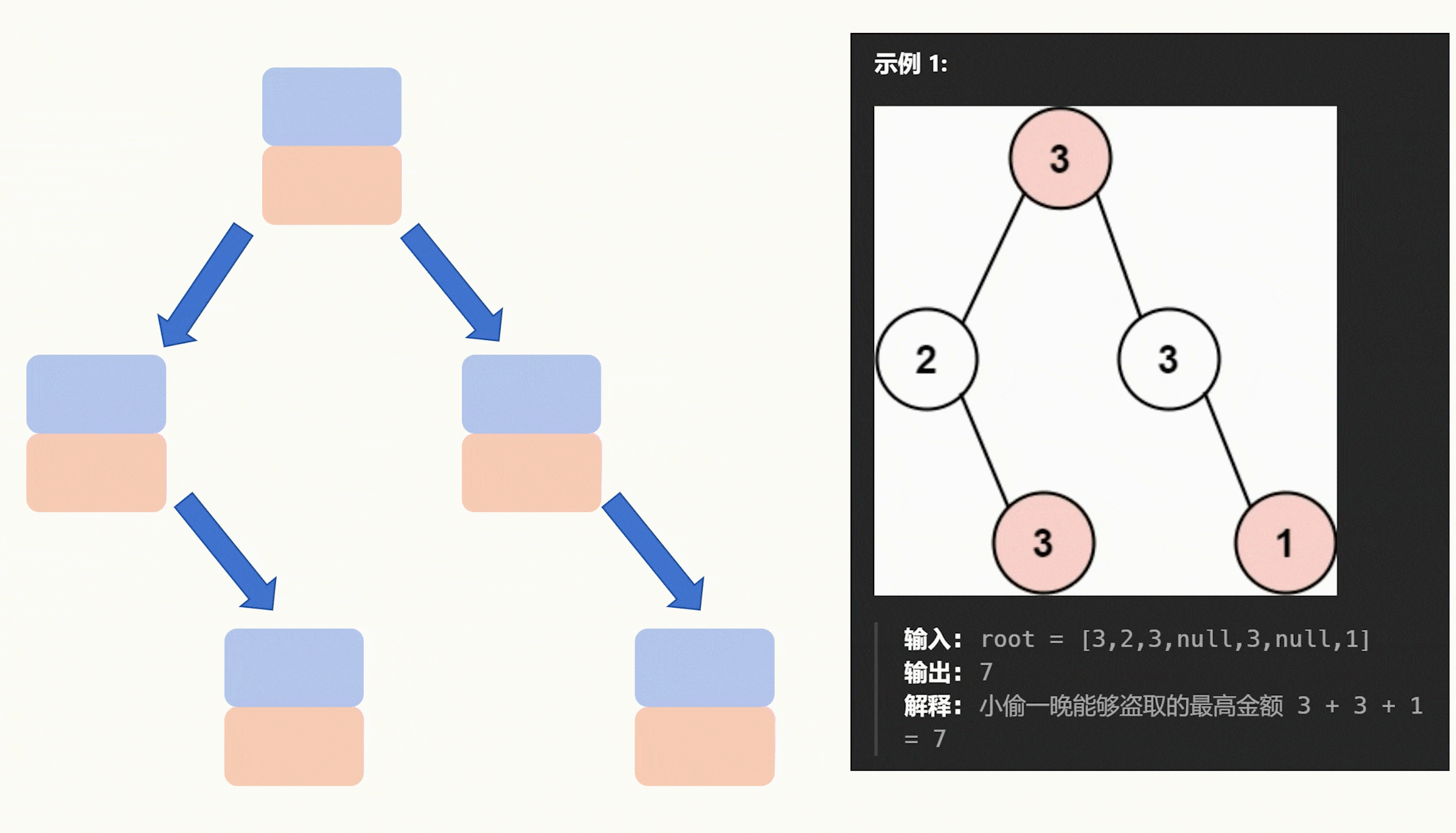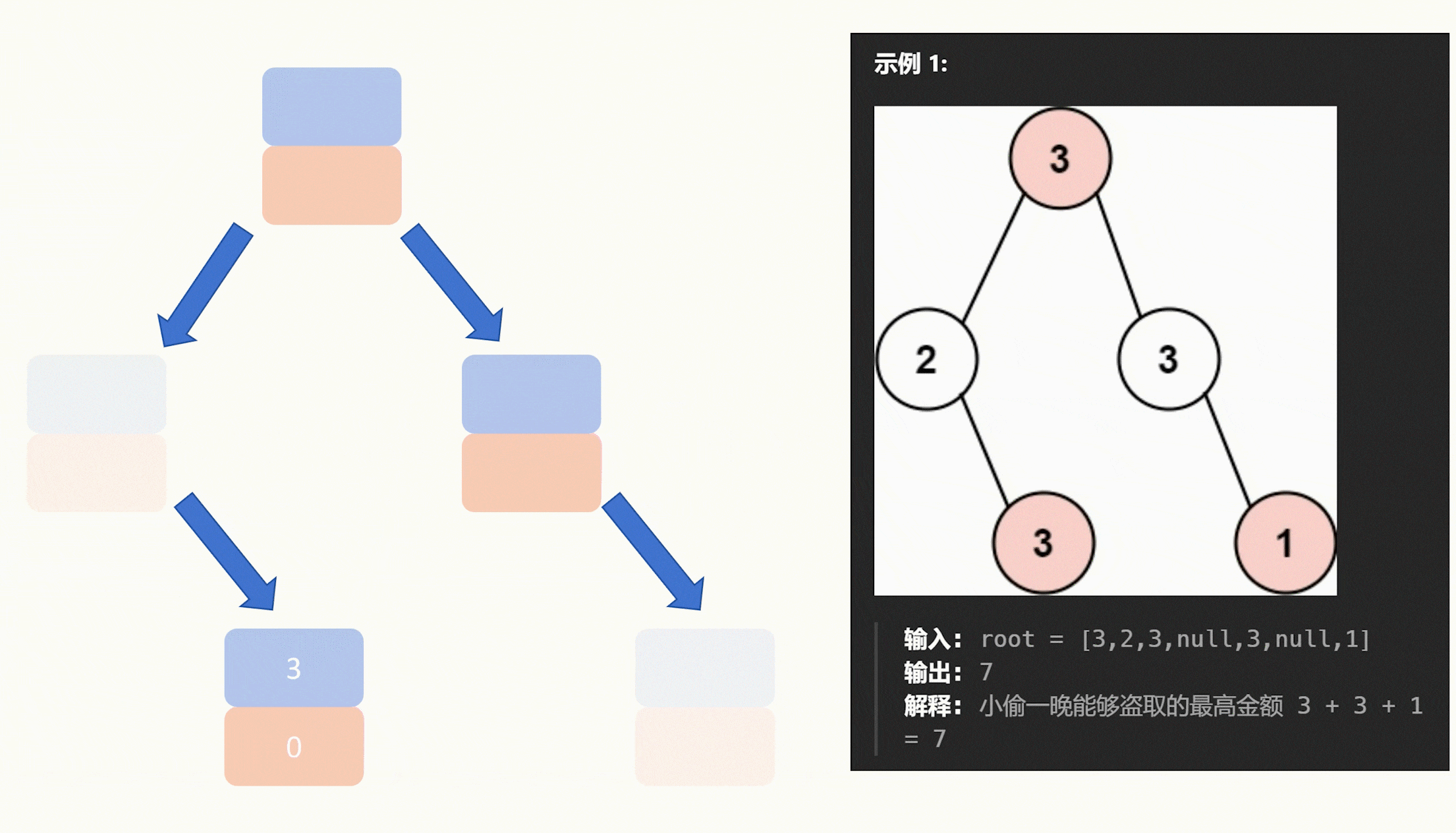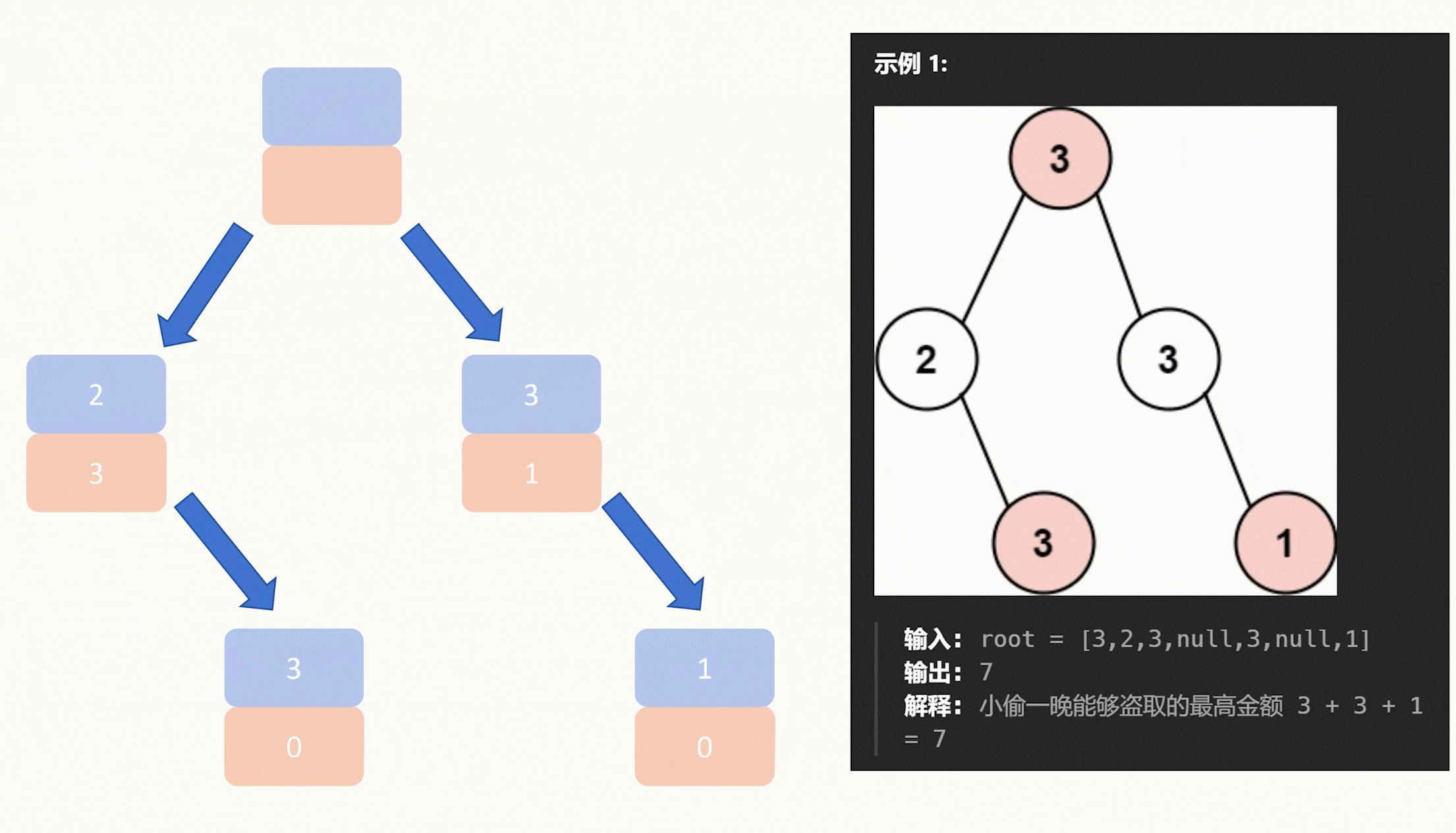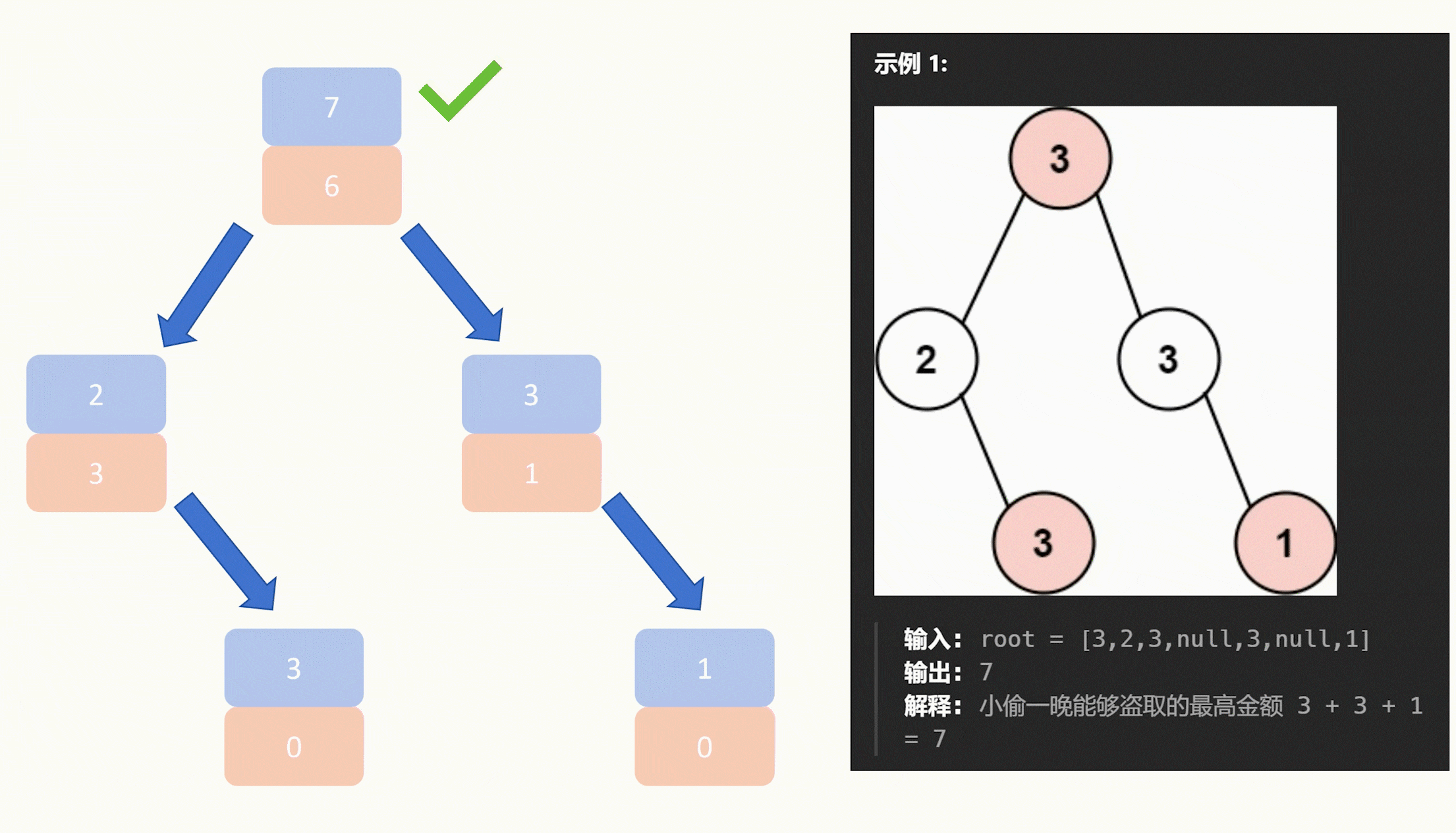
输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7
示例 2:
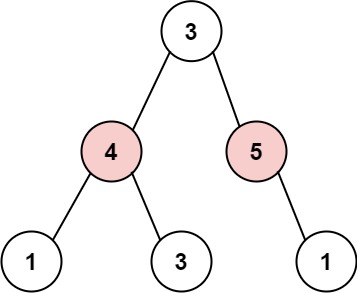
输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9
提示:
- 树的节点数在
[1, 104]范围内 0 <= Node.val <= 104
核心思想:深度搜索,判断每个节点的状态(从最下面开始判断结点状态),然后根据不同的状态进行不同的操作,要是被选中了,那么左右子树不能被选中;如果没有被选中,就是找左右子树中最大的一个进行返回
void fun(struct TreeNode*root,int *yes,int *no){
int Lyes = 0, Lno = 0;//分别表示左边子树选中、左边子树未选中
int Ryes = 0, Rno = 0;//与上同理
if(root->left != NULL){
//递归左子树
fun(root->left,&Lyes,&Lno);
}
if(root->right != NULL){
fun(root->right,&Ryes,&Rno);
}
//如果当前结点被选上了,那么就是返回左右没选上的节点的最大值加上该节点的值
*yes = Lno + Rno + root->val;
//如果当前结点没有别选上,那就从左右子树中找到更大的一颗子树
*no = max(Lyes,Lno) + max(Ryes,Rno);
}
参数是树,左边子树最大的值,右边子树最大值
首先定义四个变量分别表示左结点选中与未被选中,右节点别选中和未被选中
然后递归左子树一直到倒数第二层的左节点,然后有一棵高度为2的子树,然后判断是选中这个结点,那么就更新这个结点的值为未被选中的时候的左子树和右子树和该结点的和;如果没有选中这个结点,那么就找出左子树右子树中的最大的一个数值,更新到这个结点;右边也是同理
int rob(struct TreeNode* root){
void fun();
int max();
int yes = 0;
int no = 0;
if(root != NULL){
fun(root,&yes,&no);
}
//比较顶点结点选中与不选中的大小,返回更大的值
return max(yes,no);
}这个函数中就是找出以根节点为目标节点,找出最大值
完整代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
int rob(struct TreeNode* root){
void fun();
int max();
int yes = 0;
int no = 0;
if(root != NULL){
fun(root,&yes,&no);
}
//比较顶点结点选中与不选中的大小,返回更大的值
return max(yes,no);
}
void fun(struct TreeNode*root,int *yes,int *no){
int Lyes = 0, Lno = 0;//分别表示左边子树选中、左边子树未选中
int Ryes = 0, Rno = 0;//与上同理
if(root->left != NULL){
//递归左子树
fun(root->left,&Lyes,&Lno);
}
if(root->right != NULL){
fun(root->right,&Ryes,&Rno);
}
//如果当前结点被选上了,那么就是返回左右没选上的节点的最大值加上该节点的值
*yes = Lno + Rno + root->val;
//如果当前结点没有别选上,那就从左右子树中找到更大的一颗子树
*no = max(Lyes,Lno) + max(Ryes,Rno);
}
int max(int x,int y){
return x>=y?x:y;
}