目录

题目：

示例：

分析：

代码：

---

题目：

示例：

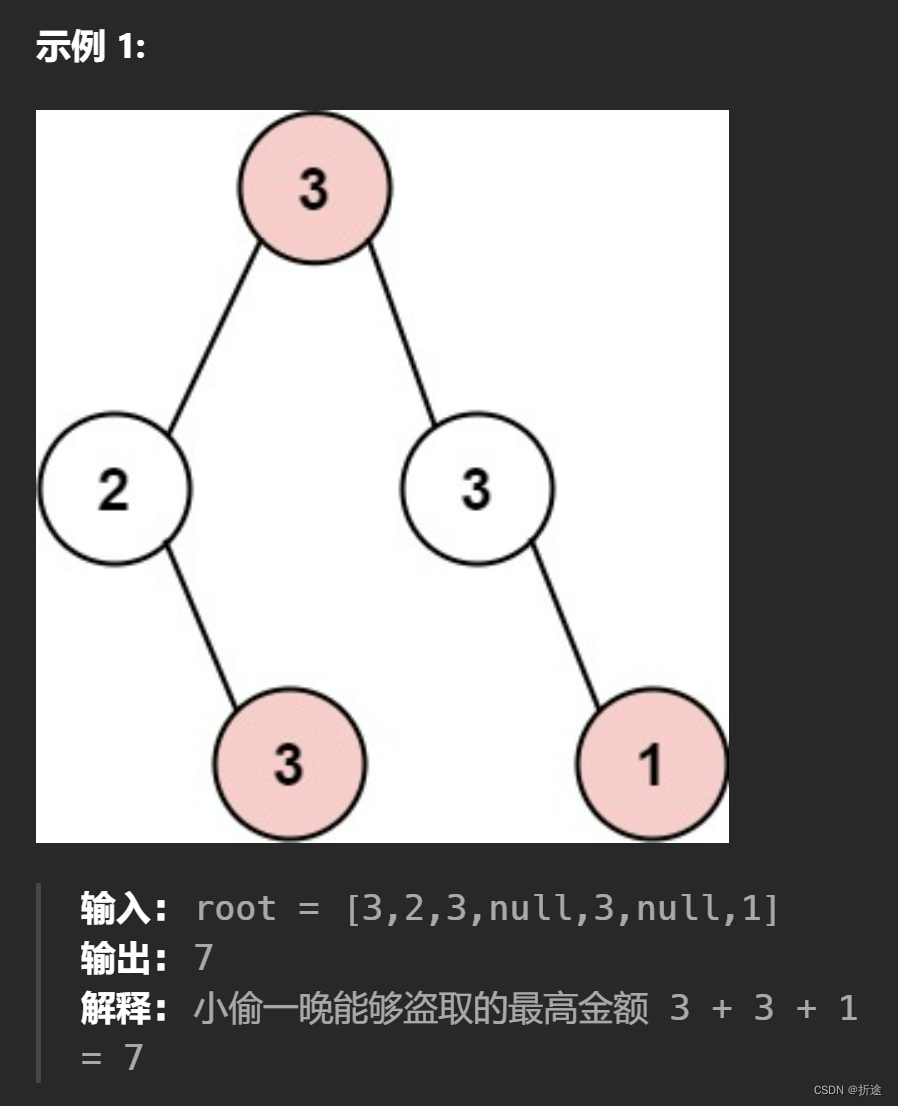
分析：

今天是打家劫舍3，明天估计就是打家劫舍4了。

今天的打家劫舍不太一样，改成二叉树了，不过规则没有变，我们还是不能偷相邻的节点。

此时房屋的排序不是像之前那样是线性的了，也就是说我们无法使用之前的常规的动态规划来解决这道题，不过我们仍可以使用动态规划的思想来解决。

动态规划本质上就是状态转移。在线性排列的房屋之中，我们dp[ i ]等于截止到第 i 间房，我们能获取的最大的值是多少。

在二叉树之中我们同样也能沿用这个dp数组的含义，不过不同的是二叉树有些许不同，因为线性房屋相邻的房屋只有左右两个。而二叉树的节点中，相邻的有父节点和两个子节点一共三个。

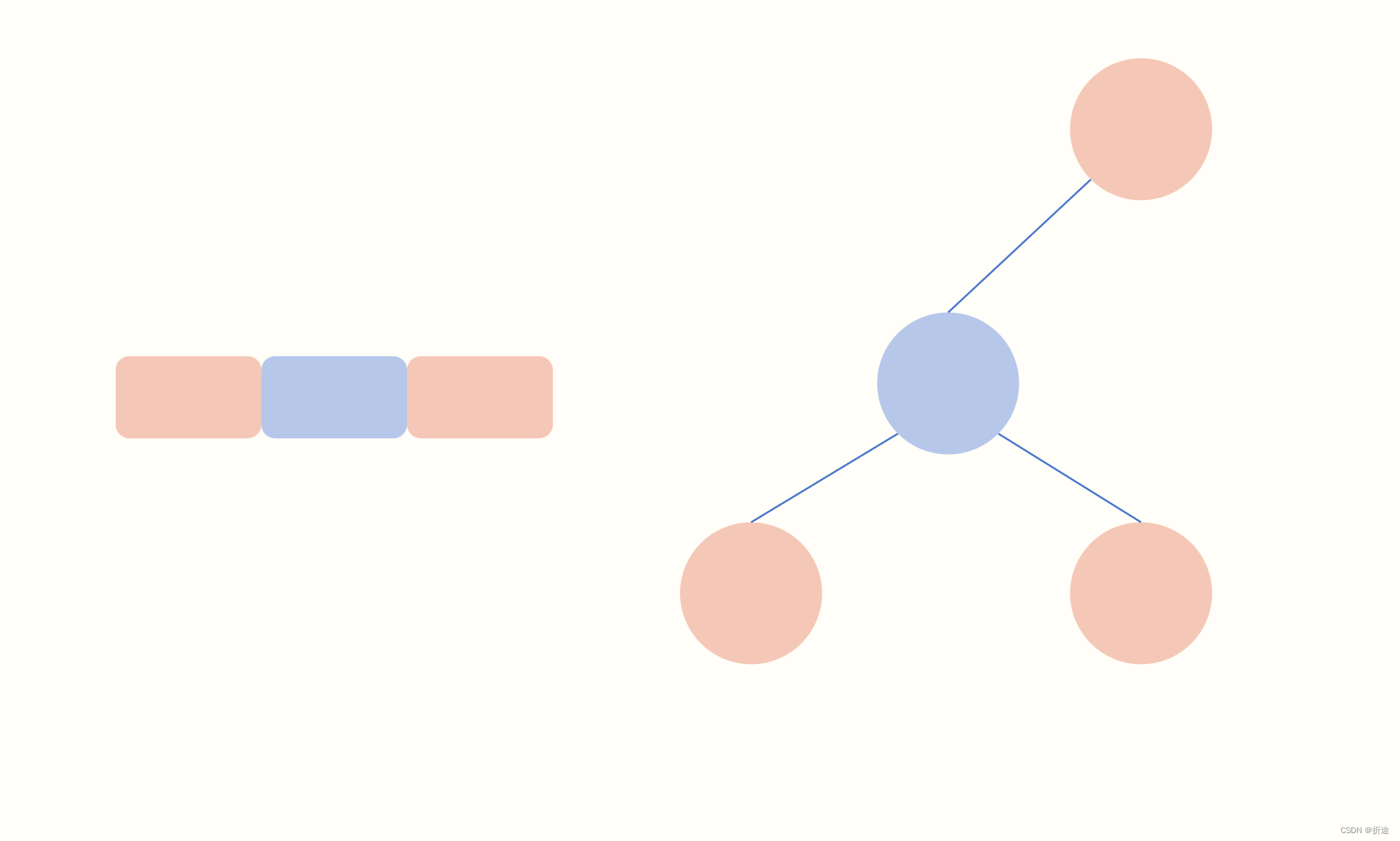
在线性表中，我选择了下标为 i 的房间，我就不能选择 i - 1 和 i + 1 。

在二叉树中，我选择了一个节点，则它的左右子节点和父节点都不能选。

那么反过来呢？我不选择当前节点，那么我就可以选择左右两个子节点和父节点。

因为有两种情况，因此此时的dp数组应该是二维的，分别存放的是我选择当前节点所能获取的最大值以及我不选择当前节点所能获取的最大值。

现在我们来找找递推公式。

如果我选择当前节点，那么我能获取的最大值就是当前节点的值，以及左右两个子节点中不选择自己节点能获取到的最大值。

如果我不选择当前节点，那么我能获取的最大值就是左右两个子节点中，能获取的最大值。

以下动图以示例一为例，大家可以结合代码看看。

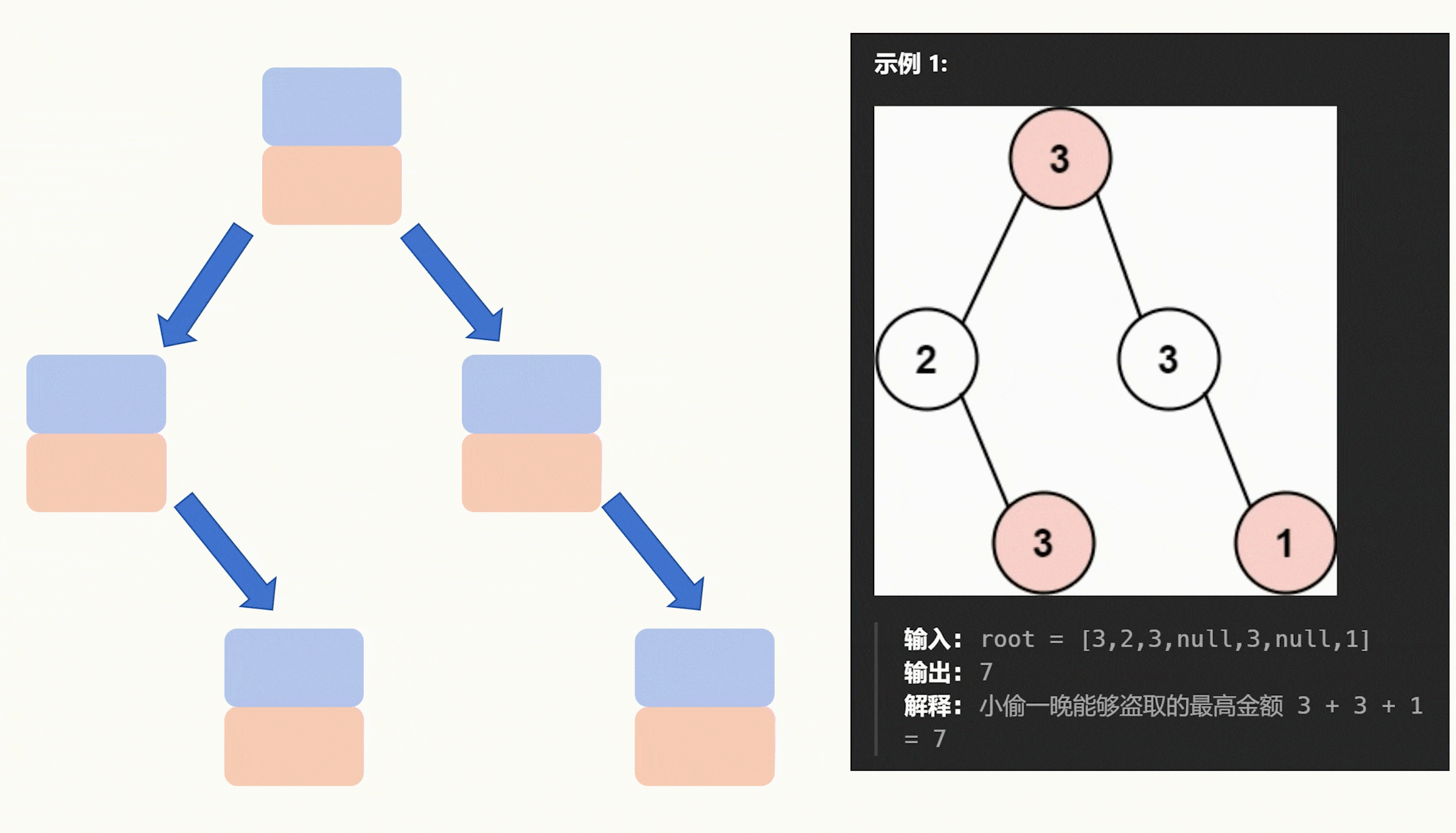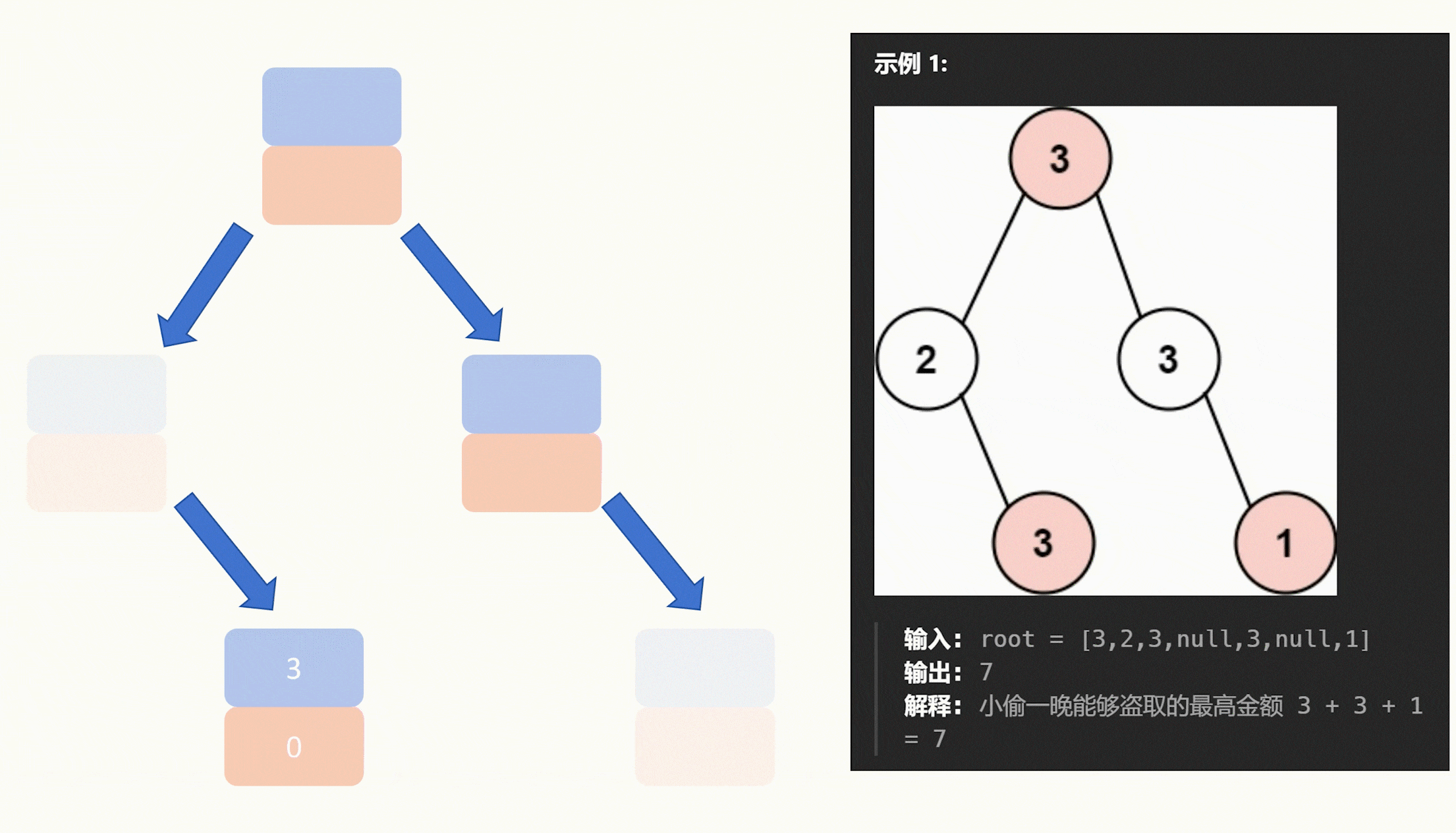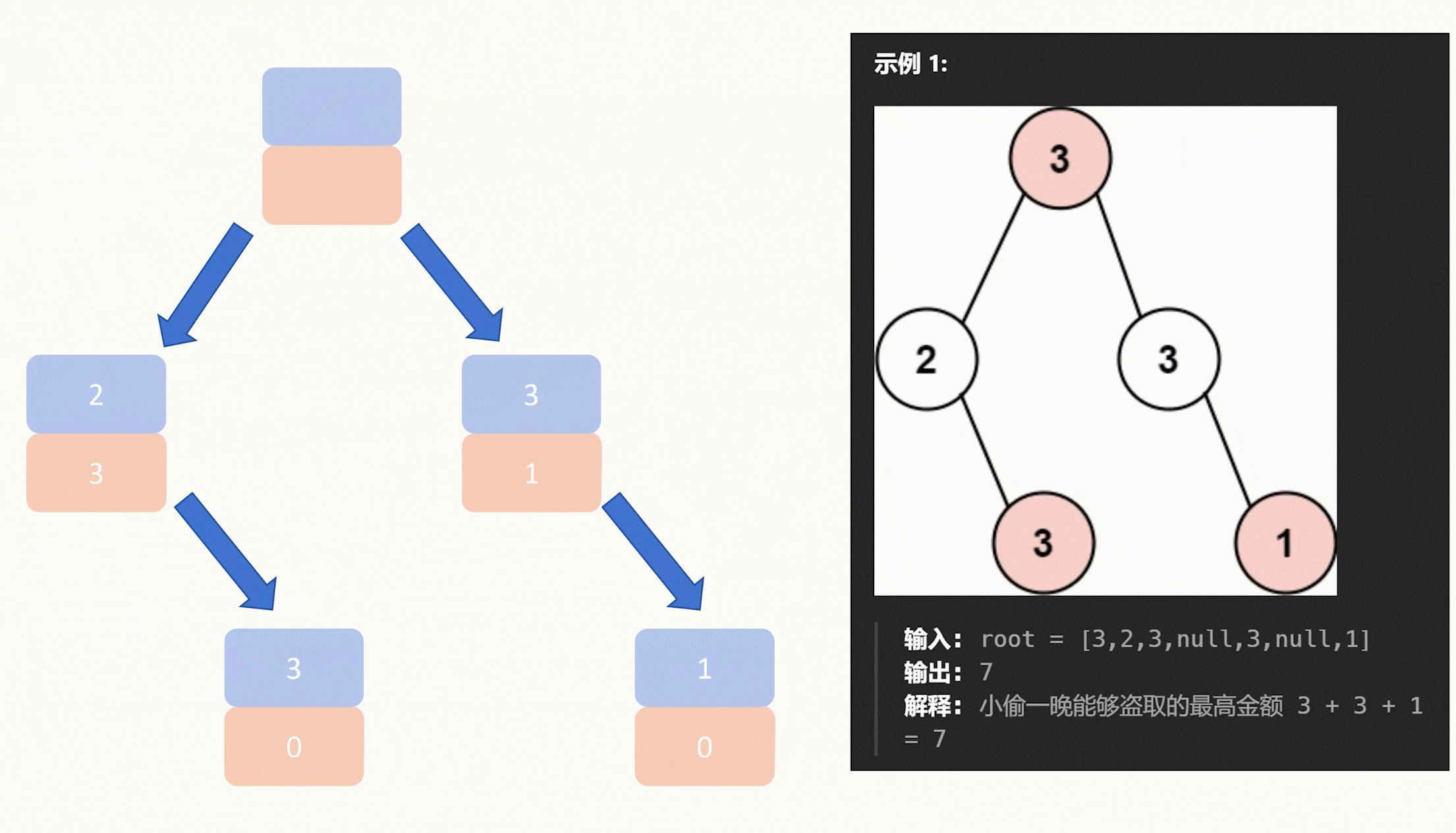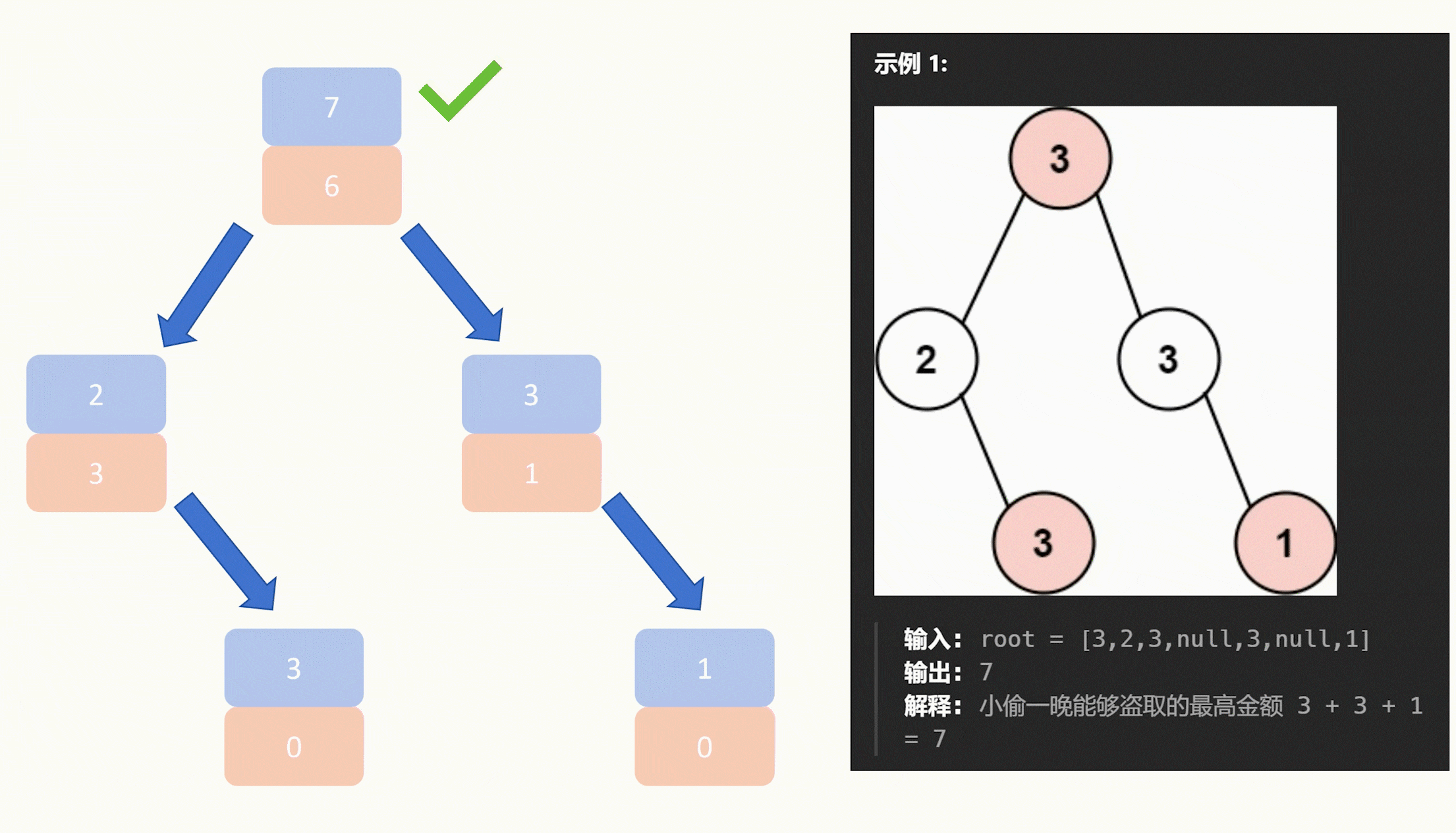
最后就是具体的做法，我们要求一个节点的能获取的最大值，我们就需要知道它的两个子节点能获取到的最大值，因此我们使用递归去遍历二叉树，至下而上去递推。

最终我们将根节点的能获取的最大值中（选择根节点能获取的最大值和不选择根节点能获取的最大值）取一个最大的返回出去。

代码：

class Solution {
public:
    //返回出去的数组一共两个元素,第一个表示偷本节点获取的最大值,第二个表示不偷本节点获取的最大值
    vector<int> find(TreeNode* root){
        //如果当前节点为空,那么偷与不偷都是0
        if(root==nullptr) return {0,0}; 
        auto l=find(root->left);
        auto r=find(root->right);
        //偷本节点获取的最大值就是本节点的值再加上两个子节点中不偷本节点的最大值(root->val+l[1]+r[1])
        //不偷本节点获取的最大值就是两个子节点中,分别取一个最大的值然后加起来.
        return {root->val+l[1]+r[1],max(l[0],l[1])+max(r[0],r[1])};
    }
    int rob(TreeNode* root) {
        vector<int>res=find(root);
        return max(res[0],res[1]);
    }
};