TypeScript逆变 ：条件、推断和泛型的应用

1 一个类型问题

有一个名为 test 的函数，它接受两个参数。第一个参数是函数 fn，第二个参数 options 受到 fn 参数的限制。乍一看，这个问题貌似并不复杂，不是吗？糊业务的时候，这种不是常见的需求嘛。

“创建一个泛型类型 Test，以确保这两个参数之间存在约束关系就完事了，睡醒再说”，就这样暗忖着，又昏昏沉沉睡过去，只有那 T extends unknown[]闯入我梦中，飘忽不定，若即若离，暗示着我再次翻车【看题时觉得简单，解题时头大如牛】的命运。

下面我们先来看看题目：

type InjectorFunction<P> = () => P;

interface Options<P> {
  injector: InjectorFunction<P>;
}

const fn1 = () => 1;
const fn2 = (p: number) => `number is: ${p}!`;
const fn3 = (p: string) => `hello ${p}!`;
const fn4 = (p?: string) => `hello ${p || 'fn4'}!`;

type Test<F extends (...args: any[]) => any = any> = (fn: F, options?: Options<Parameters<F>>) => void;

const test: Test = (fn, options) => {
  return fn(options?.injector?.());
}

// 定义 Test 函数的类型，使得下面类型成立
test(fn1);                                  // right
test(fn1, { injector: () => {} });          // error, dont need injector
test(fn2, { injector: () => 4 });           // right
test(fn3, { injector: () => 'world' });     // right
test(fn3);                                  // error, options.injector is required
test(fn4);                                  // right
test(fn4, { injector: () => 'test4' });     // right

在继续往下翻阅之前，先来typescript playground 玩呀，兄弟们。也可以用来配合本文食用哦。

2 题目规则和解法

阅读代码中的注释，我们可以得出以下题目描述和要求：

考虑函数 test，它有两个参数。第一个参数必然是一个函数 fn，而第二个参数 options 受到 fn 约束，其泛型参数是 fn的参数类型。

• 如果 fn 没有参数，则 test 不能有第二个参数 options。
• 如果 fn 有一个参数 p，则 test 必须有第二个参数 options。
• 如果 fn 的参数 p 是可选的，则第二个参数 options 也是可选的。
• options是个泛型 Options<T>， T的类型是 fn 的参数 p的类型。

在观察前三个规则后，我们初步得出了一个类似于下面结构的 test 函数，其中推断参数个数的部分需要延迟：

type Test = (...arg: unknown[]) => unknown

我们知道，使用泛型类型或条件类型可以帮助实现参数之间的约束关系。而题目中已经定义好的Test类型中，type Test<F extends (...args: any[]) => any = any> = (fn: F, options?: Options<Parameters<F>>) => void;options直接定义为可选的，并不能符合第一和第二条规则。

我们需要创建一个名为 Args<T> 的工具类型，它用于动态生成 test 函数的参数。尽管我们目前使用泛型来描述这些参数，但是我们可以使用伪代码 [FN, Opts] 来暂时表示未完成的实现。具体而言，我们将 fn 参数的类型称为 FN，将 options 参数的类型称为 Opts。

type Test = <T>(...arg: Args<T>) => unknown

首先, T 必须是个数组，如果不是数组，那它就没存在的必要了，如果是，我们先返回两个参数组成的数组好不啦。现在，可以用上前面起的小名了！略西！

type Args<T> = T extends unknown[] ? [FN, Opts] : never

其次，第一个参数必然是 fn，我们需要判断它的参数形状。先从最简单的 fn 没有参数开始。

type Args<T> = T extends unknown[] ?
    T[0] extends () => number ? [() => number]: [FN, Opts] : never

下一步，我们需要判断 T[0] 是个带有参数的函数。T[0] 是 (arg: SomeType) => unknown吗？如果是，我们还要把 SomeType 添加到 [FN, Opts]。还记得前文第四个规则吗，小 Opts 是个泛型，是个参数和 FN参数一致的泛型。

在条件类型表达式中，infer 关键字用来声明一个待推断的类型变量，将其用于 extends 条件语句中。这样可以使 TypeScript 推断出特定位置的类型，并将其应用于类型判断和条件分支中。

因此，我们可以用这个条件语句 T[0] extends (arg: infer P) => string 来表示T[0] 可以赋值给 (arg: infer P) => string。在这个条件语句中，我们使用 infer P 来声明一个类型变量 P，它用于描述 fn 的参数类型以及 Options<T> 泛型的参数类型。

type Args<T> =
  T extends unknown[] ?
    T[0] extends () => number ? [() => number]:
    T[0] extends (arg: infer P) => string ? [(arg: P) => string, Options<P>] : [FN, Opts]
  : never

在这一步，我们还需要解决一个问题，即如何判断参数是否为可选类型。

要获取函数的参数，我们可以使用 TypeScript 内置的 Parameters 类型。

Parameters<T> 类型接受一个函数类型 T，并返回该函数类型的参数类型元组。通过检查 Parameters<T> 元组的长度和元素类型，我们可以判断参数的个数和类型，并根据需要进行相应处理。

type GetParamsNum<T extends (...args: any) => any> = Parameters<T>['length'];

要判断参数形状是哪种，即有、无或薛定谔的有/无（即参数个数可以是 0，也可以是 1，或者是 0 | 1），我们可以使用以下代码来区分这三种情况：0，1，0 | 1。

type GetParamShape<T> =
  [T] extends [0] ? "无" :
  [T] extends [1] ? "有" : "薛定谔的有/无"

综上所述，让我们进一步分解这个分支：T[0] extends (arg: infer P) => string，Args 类型已经完全展开，我们可以得到以下结论：

• 当 T[0] 能够赋值给 (arg: infer P) => string 时，我们可以推断出参数类型 P 是函数 T[0] 的参数类型。
• 通过 Parameters<T[0]>，我们可以获取函数 T[0] 的参数类型元组。
• 通过判断 [Parameters<T[0]>['length']] extends[1]，我们得到函数 T[0] 必然有一个参数的分支，从而返回预期的类型 [(arg: P) => string, Options<P>]。
• 如果条件不符合，返回预期的类型 [(arg?: P) => unknown, Options<P>?]， arg是可选的，Options也是可选的。

Args 类型的完整定义如下：

type Args<T> =
  T extends unknown[] ?
  T[0] extends () => number ? [() => number]:
  T[0] extends (arg: infer P) => string ? [Parameters<T[0]>['length']] extends[1] ? [(arg: P) => string, Options<P>] : 
  [(arg?: P) => unknown, Options<P>?]
  : never  : never

现在，根据前面的 type Test = <T>(...arg: Args<T>) => unknown，让我们对 test 函数进行进一步改造。

type Test = <T>(...arg: Args<T>) => unknown

const test: Test = (...args) => {
  const [fn, options] = args
  return fn(options?.injector?.())
}

在这个改造后的 test 函数中，我们接受一个参数数组 args，其中包含了函数 fn 和 options 参数。我们使用数组解构赋值将这两个参数提取出来。

我们已经完成了类型定义的重新定义以及函数的改造，现在让我们来看看是否能够得到预期的类型推断和错误。

3 第一次翻车

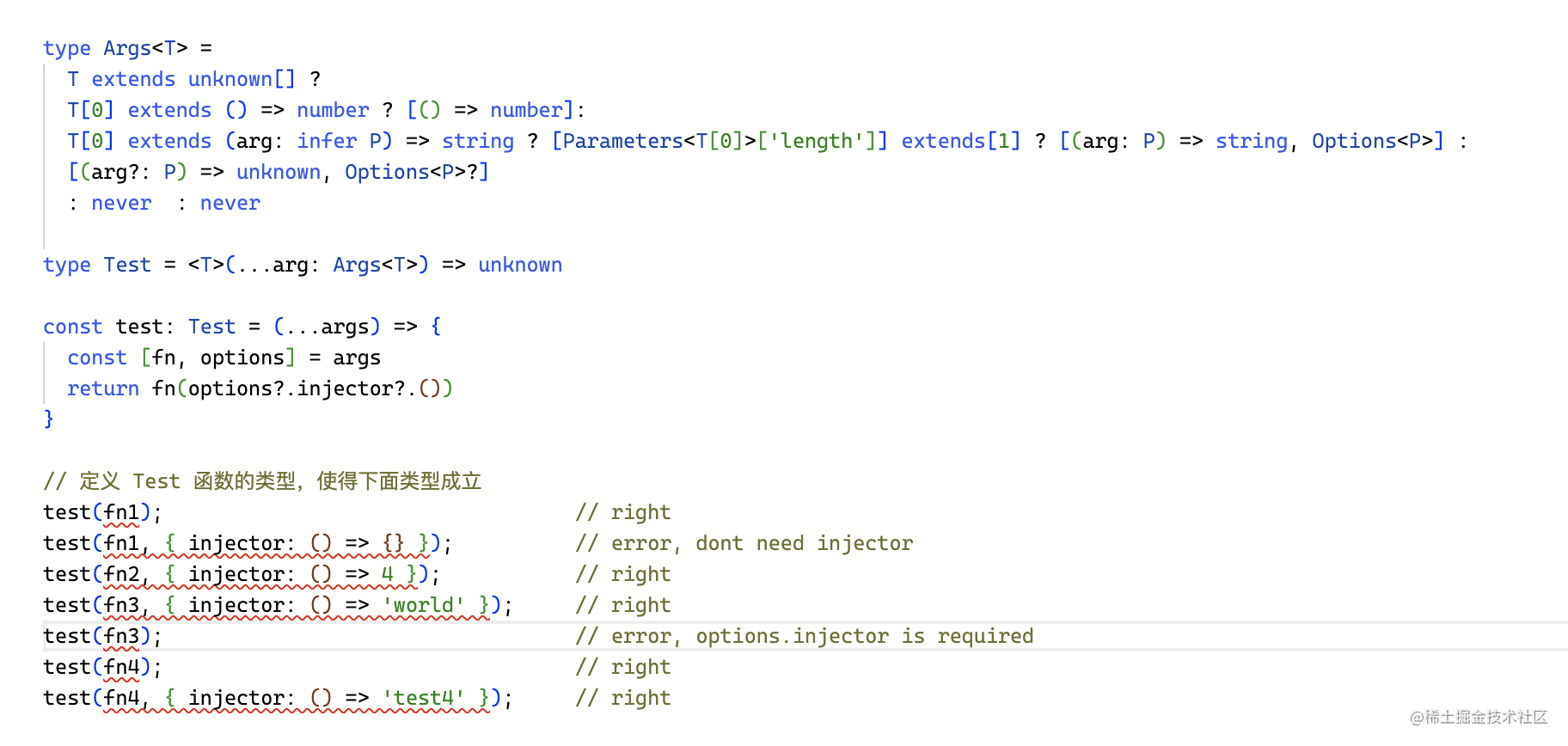
每个调用都报错了。一个方案是在调用的时候指定泛型参数，但这样做就很麻烦，并且毫不意外地被大佬嫌弃了。那就开始对 Test 进行进一步改造。

这次的改造将进一步简化 Args 类型，使其看起来更加一目了然。它接受一个泛型参数 T，该参数是一个数组类型，表示函数的参数列表。根据不同的参数个数，我们进行不同的类型转换：

• 如果参数列表为空，即 T extends []，则表示函数没有参数。在这种情况下，test没有其他参数，即 []。
• 如果参数列表只有一个元素 P，即 T extends [infer P]，则表示函数只有一个参数。我们将该参数的类型进行转换为 Options<P>，即一个带有 P 类型的 Options 类型的元组，即 [Options<P>]。
• 对于其他情况，我们将整个参数列表定义为一个可选的 Options<string> 类型的元组，即 [Options<string>?]。

最后，我们定义了一个 Test 类型，它是一个高阶函数类型，接受一个函数 T 作为第一个参数，以及根据函数参数列表进行转换的元组类型 Args<Parameters<T>>。该类型表示函数的参数列表可能有多个，并且根据参数个数的不同应用不同的转换类型。现在，我们就可以直接传入函数 fn 和它的参数来调用 Test 函数，不再需要在每次调用的时候指定 fn 类型。

type Args<T extends unknown[]> =
  T extends [] ? [] :
  T extends [infer P] ? [Options<P>] : [Options<T[0]>?]

type Test = <T extends (...arg: any[]) => unknown>(...args: [T, ...Args<Parameters<T>>]) => unknown

这里用上了any 和 unknown，给泛型T指定为带有任意参数的函数类型。应该避免使用万能类型 any，因为它绕过了类型检查，降低了类型安全性。然而在此处，我们无法替换 any 为 unknown，类型的位置影响逆变协变，函数参数通常处于逆变的位置，子类型（更具体的类型）不能赋值给父类型（更宽泛的类型）。而unknown 是所有类型的父类型。

看广场吧，期待其它解法分享啊兄弟们。等你们来玩啊。

4 真正的规则

• 当 fn 没有参数时，options 是可选的，但没有 injector 字段。
• 当 fn 有参数且参数为必填时，options.injector 也是必填的，且injector 的返回类型为 fn 的参数类型。
• 当 fn 有参数但参数为可选时，options 是可选的，injector 也是可选的，且返回字符串。
• options可能有其它属性，但具体是什么属性并没有明确指定。因此，我们可以假设其他属性只有一个 weight 属性。

预期错误如下所示：

// 定义 Test 函数的类型，使得下面类型成立
test(fn1);                                  // right
test(fn1, { weight: 10 });                  // right
test(fn1, { injector: () => {} });          // error, dont need injector
test(fn2, { injector: () => 4 });           // right
test(fn3, { injector: () => 'world' });     // right
test(fn3);                                  // error, options.injector is required
test(fn3, { injector: () => 4 });           // error
test(fn4);                                  // right
test(fn4, { injector: () => 'test4' });     // right
test(fn4, { injector: () => undefined });   // error

为了符合上述规则，我们对泛型工具类型 Args进行了一些分支上的改造处理：

• 如果 fn 参数列表为空，即 T extends []，则剩余的参数列表定义为一个可选的 OtherOpts 类型的元组，即 [OtherOpts?]。
• 如果fn参数列表只有一个元素 P，即 T extends [infer P]。我们将该参数的类型进行转换为 Options<P>，指定 options.injector 的返回类型为 fn 参数类型 P。
• 对于其它情况，我们将整个参数列表定义为一个可选的 Options<string> 类型的元组，即 [Options<string>?]。

Test 高阶函数类型保持不变。

interface OtherOpts  {
  weight: number;
}

type Args<T extends unknown[]> =
  T extends [] ? [OtherOpts?] :
  T extends [infer P] ? [Options<P>] : [Options<string>?]