目录

题目：

示例：

分析：

代码：

---

题目：

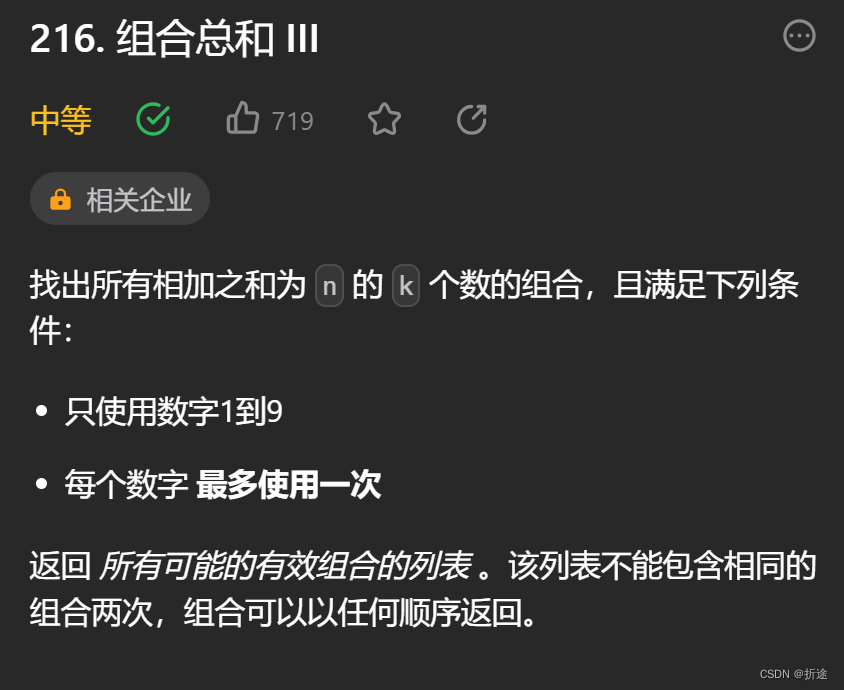
示例：

分析：

题目让我们找出长度为k并且总和为n的所有组合，我们能用的元素只有1~9。

那么这种要求排列组合的题，基本是是离不开递归回溯的。

那么由于我们能用的元素是固定且有序的，那么我们可以给递归函数传递我们本次递归要用到的元素，从1开始传递，每次进入下一轮递归就+1再传过去，直到递归到了10，那么根据题目要求，我们是不能使用10以上的数字的，那么我们就停止递归。

另外递归要传的参数还有临时的排列数组，如果递归的时候发现临时排列数组的长度为k了，并且总和等于n了，那么我们就加入到答案列表里，然后结束递归。

为了减少重复计算，我们也可以把临时数组里的元素总和也当作参数传给递归函数，这样就不用每次判断总和是否等于n的时候还要遍历临时数组算一边。

具体可以参考代码。

代码：

class Solution {
public:
    vector<vector<int>> res;
    void digui(const int &k,const int &n,vector<int>temp,const int &sum,const int &index){
        if(temp.size()==k){ //临时组合长度满足要求
            if(sum==n) res.push_back(temp); //总和也满足要求就加入到答案里
            return;
        }
        if(sum>n || index >=10) return; //如果总和大于要求或者是接下来要用到的数>=10不符合要求就退出
        digui(k,n,temp,sum,index+1);    //进入下一层递归但是不加入本次的数字
        temp.push_back(index);
        digui(k,n,temp,sum+index,index+1);  //进入下一层递归,但是临时组合加入本轮的数字
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        digui(k,n,vector<int>(0),0,1);
        return res;
    }
};