week 1

1. 找出数组中重复的数字

题目

给定一个长度为 n 的整数数组 nums，数组中所有的数字都在 0∼n−1 的范围内。

数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。

请找出数组中任意一个重复的数字。

注意：如果某些数字不在 0∼n−1 的范围内，或数组中不包含重复数字，则返回 -1；

数据范围

0≤n≤1000

样例

给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。
返回 2 或 3。

题解

(数组遍历) O(n)

首先遍历一遍数组，如果存在某个数不在0到n-1的范围内，则返回-1。

下面的算法的主要思想是把每个数放到对应的位置上，即让 nums[i] = i。

从前往后遍历数组中的所有数，假设当前遍历到的数是 nums[i]=x，那么：

• 如果x != i && nums[x] == x，则说明 x 出现了多次，直接返回 x 即可；
• 如果nums[x] != x，那我们就把 x 交换到正确的位置上，即 swap(nums[x], nums[i])，交换完之后如果nums[x] != x，则重复进行该操作。由于每次交换都会将一个数放在正确的位置上，所以swap操作最多会进行 n 次，不会发生死循环。

循环结束后，如果没有找到任何重复的数，则返回-1。

时间复杂度分析

每次swap操作都会将一个数放在正确的位置上，最后一次swap会将两个数同时放到正确位置上，一共只有 n 个数和 n 个位置，所以swap最多会进行 n−1次。所以总时间复杂度是 O(n)。

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int n = nums.size();
        for (auto x : nums)
            if (x < 0 || x > n - 1)
                return -1;
                
        for (int i = 0; i < n; i++) {
            while (nums[i] != nums[nums[i]])    //注意，这里是while，一直交换
                swap(nums[i], nums[nums[i]]);
            if (nums[i] != i)
                return nums[i];
        }
        return -1;
    }
};

2. 不修改数组找出重复的数字

题目

给定一个长度为 n+1 的数组nums，数组中所有的数均在 1∼n 的范围内，其中 n≥1。

请找出数组中任意一个重复的数，但不能修改输入的数组。

数据范围

1≤n≤1000

样例

给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。
返回 2 或 3。

题解

(分治，抽屉原理) O(nlogn)

这道题目主要应用了抽屉原理和分治的思想。

抽屉原理：n+1 个苹果放在 n 个抽屉里，那么至少有一个抽屉中会放两个苹果。

用在这个题目中就是，一共有 n+1 个数，每个数的取值范围是1到n，所以至少会有一个数出现两次。

然后我们采用分治的思想，将每个数的取值的区间[1, n]划分成[1, n/2]和[n/2+1, n]两个子区间，然后分别统计两个区间中数的个数。
注意这里的区间是指 数的取值范围，而不是 数组下标。

划分之后，左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度。

这个可以用反证法来说明：如果两个区间中数的个数都小于等于区间长度，那么整个区间中数的个数就小于等于n，和有n+1个数矛盾。

因此我们可以把问题划归到左右两个子区间中的一个，而且由于区间中数的个数大于区间长度，根据抽屉原理，在这个子区间中一定存在某个数出现了两次。

依次类推，每次我们可以把区间长度缩小一半，直到区间长度为1时，我们就找到了答案。

复杂度分析

1. 时间复杂度：每次会将区间长度缩小一半，一共会缩小 O(logn) 次。每次统计两个子区间中的数时需要遍历整个数组，时间复杂度是 O(n)。所以总时间复杂度是 O(nlogn)。
2. 空间复杂度：代码中没有用到额外的数组，所以额外的空间复杂度是 O(1)。

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int l = 1, r = nums.size() - 1; //要将每个数的取值区间[1,n]划分成两个子区间，所以要-1
        while (l < r) {
            int mid = l + r >> 1; // 划分的区间：[l, mid], [mid + 1, r]
            int s = 0;
            for (auto x : nums)
            	if (x >= l && x <= mid) s++;
            	//s += x >= l && x <= mid;
           		// 先判断(x >= l && x <= mid),再 s += ***
            if (s > mid - l + 1)
                r = mid;
            else
                l = mid + 1;
        }
        return r;  //
    }
};

3. 二维数组中的查找

题目

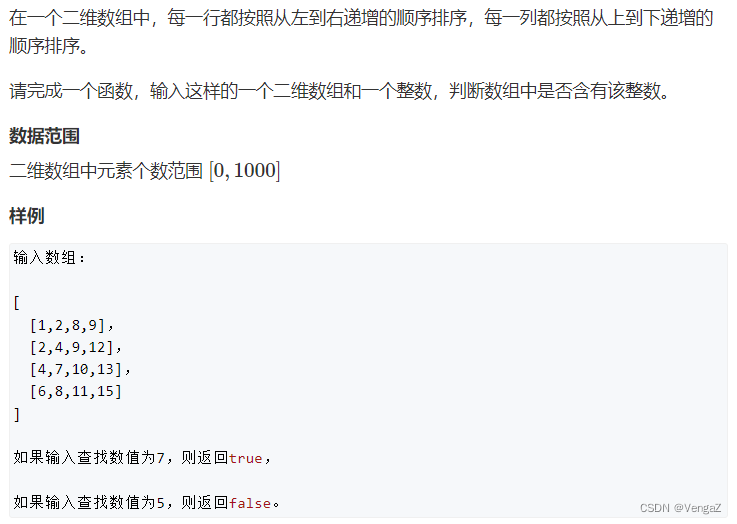
题解

(单调性扫描) O(n+m)

核心在于发现每个子矩阵右上角的数的性质：

• 如下图所示，x左边的数都小于等于x，x下边的数都大于等于x。

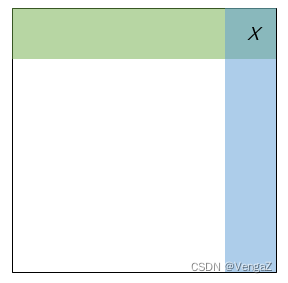
因此我们可以从整个矩阵的右上角开始枚举，假设当前枚举的数是 x：

• 如果 x 等于target，则说明我们找到了目标值，返回true；
• 如果 x 小于target，则 x 左边的数一定都小于target，我们可以直接排除当前一整行的数；
• 如果 x 大于target，则 x 下边的数一定都大于target，我们可以直接排除当前一整列的数；

排除一整行就是让枚举的点的横坐标加一，排除一整列就是让纵坐标减一。
当我们排除完整个矩阵后仍没有找到目标值时，就说明目标值不存在，返回false。

时间复杂度分析

每一步会排除一行或者一列，矩阵一共有 n 行，m 列，所以最多会进行n+m 步。所以时间复杂度是 O(n+m)。

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if (array.empty() || array[0].empty()) return false;
        int i = 0, j = array[0].size() - 1;  // j 初始为右上角的位置
        while (i < array.size() && j >= 0) {
            if (array[i][j] == target) return true;
            if (array[i][j] > target) --j;  // 锁定当前行，排除当前列
            else ++i;  // 排除当前行，往下搜索
        }
        return false;
    }
};

4.替换空格

题目

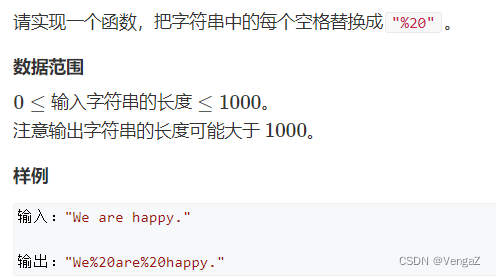
题解

(线性扫描) O(n)

这个题在C++里比较好做，我们可以从前往后枚举原字符串：

• 如果遇到空格，则在string类型的答案中添加 "%20"；
• 如果遇到其他字符，则直接将它添加在答案中；

但在C语言中，我们没有string这种好用的模板，需要自己malloc出char数组来存储答案。
此时我们就需要分成三步来做：

1. 遍历一遍原字符串，计算出答案的最终长度；
2. malloc出该长度的char数组；
3. 再遍历一遍原字符串，计算出最终的答案数组；

时间复杂度分析

原字符串只会被遍历常数次，所以总时间复杂度是 O(n)。

class Solution {
public:
    string replaceSpaces(string &str) {
        string res;
        for (auto x : str)
            if (x == ' ')
                res += "%20";
            else 
                res += x;
        return res;
    }
};

(双指针扫描) O(n)

在部分编程语言中，我们可以动态地将原数组长度扩大，此时我们就可以使用双指针算法，来降低空间的使用：

1. 首先遍历一遍原数组，求出最终答案的长度length；
2. 将原数组resize成length大小；
3. 使用两个指针，指针i指向原字符串的末尾，指针j指向length的位置；
4. 两个指针分别从后往前遍历，如果str[i] == ' '，则指针j的位置上依次填充'0', '2', '%'，这样倒着看就是"%20"；如果str[i] != ' '，则指针j的位置上填充该字符即可。

由于i之前的字符串，在变换之后，长度一定不小于原字符串，所以遍历过程中一定有i <= j，这样可以保证str[j]不会覆盖还未遍历过的str[i]，从而答案是正确的。

时间复杂度分析

原字符串只会被遍历常数次，所以总时间复杂度是 O(n)。

class Solution {
public:
    string replaceSpaces(string &str) {
        int len = 0;
        for (auto c : str)
            if (c == ' ') len += 3;
            else len++;
                
        //str.size() 字符串中有几个字符，大小就为几    
        //定义两个指针，字符串的长度和实际下标位置差1
        int i = str.size() - 1, j = len - 1;  
        str.resize(len);  //调整字符串大小
        while (i >= 0) {
            if (str[i] == ' ') {
                str[j--] = '0';
                str[j--] = '2';
                str[j--] = '%';
            }
            else str[j--] = str[i];
            i--;
        }
        return str;
    }
};

5.从尾到头打印链表

题目

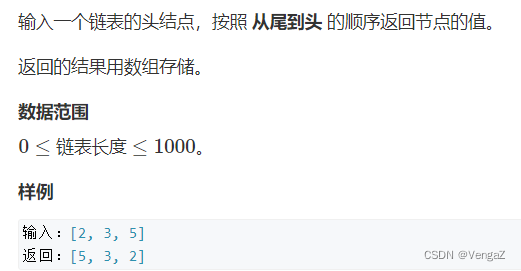
题解

(遍历链表) O(n)

单链表只能从前往后遍历，不能从后往前遍历。

因此我们先从前往后遍历一遍输入的链表，将结果记录在答案数组中。
最后再将得到的数组逆序即可。

语法补充：

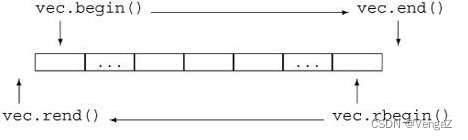
begin
语法：iterator begin();
解释：begin()函数返回一个迭代器,指向字符串的第一个元素.

end
语法：iterator end();
解释：end()函数返回一个迭代器，指向字符串的末尾(最后一个字符的下一个位置).

rbegin
语法：const reverse_iterator rbegin();
解释：rbegin()返回一个逆向迭代器，指向字符串的最后一个字符。

rend
语法：const reverse_iterator rend();
解释：rend()函数返回一个逆向迭代器，指向字符串的开头（第一个字符的前一个位置）。

时间复杂度分析
链表和答案数组仅被遍历了常数次，所以总时间复杂度是 O(n)。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> printListReversingly(ListNode* head) {
        vector<int> res;
        while (head) {
            res.push_back(head->val);
            head = head->next;
        }
        return vector<int>(res.rbegin(), res.rend()); //反向迭代器
    }
};