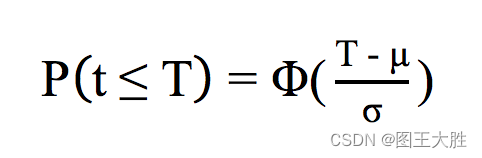
完整程序:
%有多普勒频移的海底混响点散射模型
clear all; close all; clc
H=100; %海水深度
D=50; %合置声纳深度
c=1500; %声速
azm=pi/6; %水平方位角
u=-27; %垂直散射系数
v=20; %声纳运动速度
fs=25000; %采样频率
f0=4000; %中心频率
T=0.001; %仿真步长
rou=0.5; % 0.85; %散射体密度
startt=0.08; %混响起始时间
endt=0.5; %混响起始时间
t=0:1/fs:endt-1/fs;
Nt=length(t);
Rb1=zeros(size(t));
R1=zeros(size(t));
t1=0.05;
ts=0:1/fs:t1-1/fs;
s1=exp(1i*2.*pi.*f0.*ts); %CW信号
Ns=length(ts);
% 信号时域
figure(1);
plot(ts,real(s1));
axis([0 0.06 -1 1]); %axis([xmin xmax ymin ymax])
xlabel('时间/s');
ylabel('幅度');
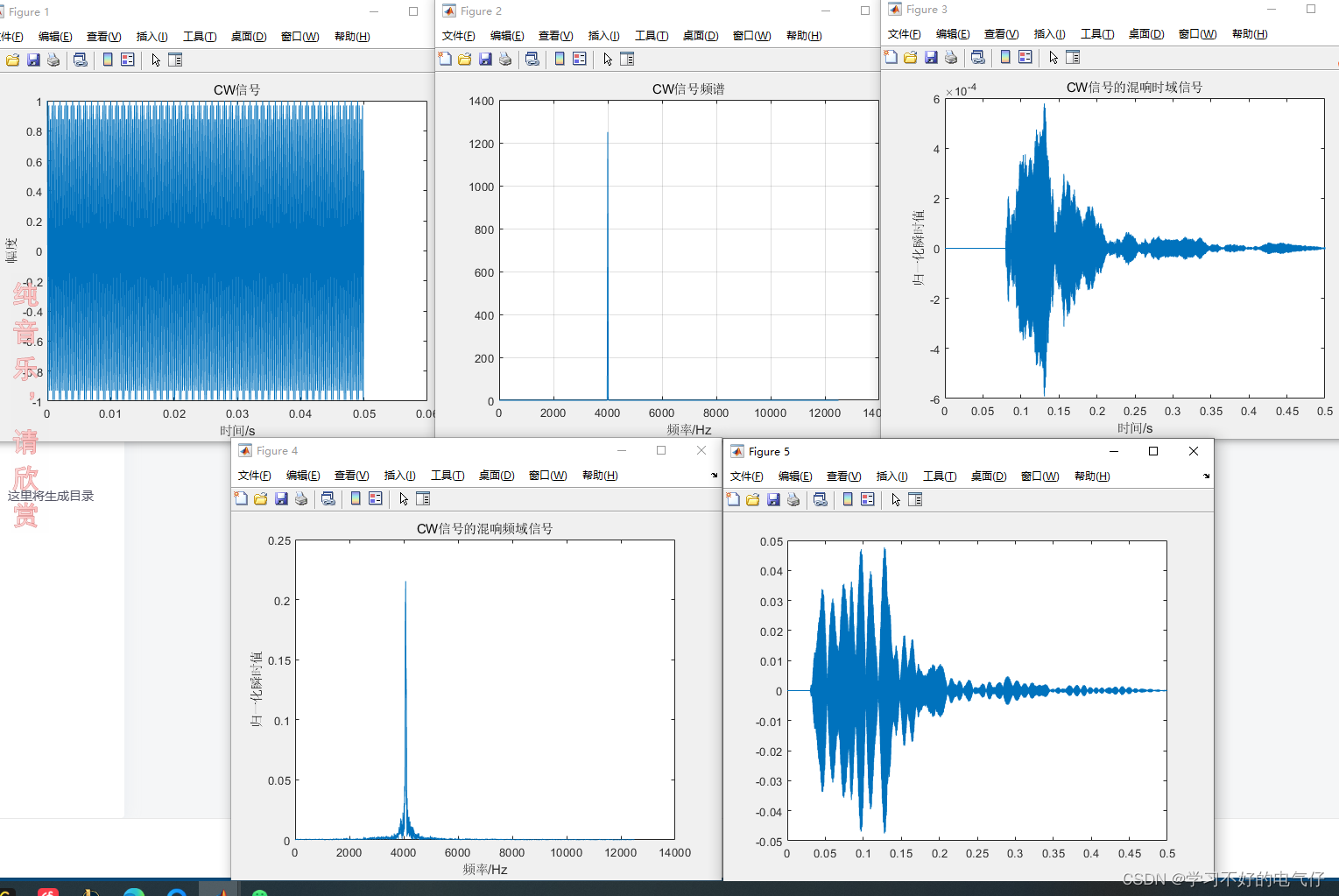
title('CW信号');
%信号频谱
X1=abs(fft(s1));
figure(2);
f=fs*(0:Ns/2)/Ns;
plot(f,X1(1:Ns/2+1));
xlabel('频率/Hz');
title('CW信号频谱')
grid on;%添加网格
m=20; %m次运算取平均
for i=1:m
for tr=startt:T:endt
r1=tr*c/2;
r2=(tr+T)*c/2;
As=(r2^2-r1^2)*azm/2;
Na=poissrnd(As*rou,1,1); %产生均值为面积的按泊松分布的一个数
r=r1+rand(1,Na)*(r2-r1);
phi=rand(1,Na)*2*pi;
alf=-pi/12+pi/6.*rand(1,Na);
for n=1:Na
d=r(n);
%计算多普勒频移
cosbt=(sqrt((r(n))^2-D^2))/r(n);
fd1=2*v/c*f0*cos(alf(n))*cosbt;
s1p=exp(1i*2.*pi.*(f0+fd1).*ts);%多普勒频移相当于对入射波进行了频移
Nrt=fix(d/c*2*fs);%取整
Sr=sqrt(10^(u/10))*(H-D)/d; %散射损失,采用兰伯特(Lambert)定律
Fr=1/d; %传播损失
h=Sr*Fr^2*exp(1i*phi(n));
if Nrt+Ns>Nt
Rb1(Nrt+1:Nt)=Rb1(Nrt+1:Nt)+s1p(1:Nt-Nrt).*h;
else
Rb1(Nrt+1:Nrt+Ns)=Rb1(Nrt+1:Nrt+Ns)+s1p.*h;
end
end
end
R1=R1+Rb1;
end
%混响时域信号
R1=R1/m;
Rr1=real(R1);
figure(3);
plot(t,Rr1);
xlabel('时间/s');
ylabel('归一化瞬时值');
title('CW信号的混响时域信号');
%混响频谱
F1=abs(fft(Rr1));
figure(4);
f1=fs*(0:Nt/2)/Nt;
plot(f1,F1(1:Nt/2+1));
xlabel('频率/Hz');
ylabel('归一化瞬时值');
title('CW信号的混响频域信号');
%%%%%%求多普勒%%%%%%%%%%%%%%%%%%%%%%%
tao=0.002;
fai=pi/6;
%%%找底位置%%%%%%%
tc=0:1/fs:endt-1/fs;
cpy=exp(1i*2*pi*f0*tc).*(tc>0 & tc<t1);
CPY=conj(fft(cpy));
R2=fft(R1);
crr=ifft(R2.*CPY);
figure(5)
plot(t,real(crr))
[~,bt]=max(real(crr));
tn=tao*fs;
x1=R1(bt:end-tn);
x2=R1(bt+tn:end);
xout=x1*x2';
fb=abs(angle(xout)/2/pi/tao)
vout=fb*c/2/cos(fai)/f0