题目
光栅化一个三角形
1. 创建三角形的 2 维 bounding box。
2. 遍历此 bounding box 内的所有像素(使用其整数索引)。然后,使用像素中心的屏幕空间坐标来检查中心点是否在三角形内。
3. 如果在内部,则将其位置处的插值深度值 (interpolated depth value) 与深度缓冲区 (depth buffer) 中的相应值进行比较。
4. 如果当前点更靠近相机,请设置像素颜色并更新深度缓冲区 (depth buffer)。
题解
本次作业需要实现代码框架中的两个接口:
void rst::rasterizer::rasterize_triangle(const Triangle& t);
static bool insideTriangle(int x, int y, const Vector3f* _v);
1. 在2D空间中,计算一个三角形的轴对称boundbox
只需要计算出三角形的三个顶点坐标中,x最大最小值,y最大最小值。即
(
x
m
i
n
,
y
m
i
n
)
,
(
x
m
a
x
,
y
m
a
x
)
(x_{min},y_{min}),(x_{max},y_{max})
(xmin,ymin),(xmax,ymax)
使用<math.h>库实现如下:
int xMin, yMin, xMax, yMax;
xMin = std::floor(std::min(std::min(v[0].x(),v[1].x()),v[2].x()));
yMin = std::floor(std::min(std::min(v[0].y(), v[1].y()), v[2].y()));
xMax = std::ceil(std::max(std::max(v[0].x(), v[1].x()), v[2].x()));
yMax = std::ceil(std::max(std::max(v[0].y(), v[1].y()), v[2].y()));
注意:顶点坐标都是浮点数,但是我们计算出的包围盒必须是整型。左上角下取整,右下角上去整。
2. 判断像素的中心点是否在三角形内部
其实方法有很多种,具体可以参考这个博客。
最常用最高效的有两种:重心坐标法和向量叉积。
本次作业选用向量叉积法:
代码如下
static bool insideTriangle(int x, int y, const Vector3f* _v)
{
// TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
auto v0_v1 = _v[1] - _v[0];
auto v1_v2 = _v[2] - _v[1];
auto v2_v0 = _v[0] - _v[2];
auto v0_P = Vector3f(x, y, _v[0].z()) - _v[0];
auto v1_P = Vector3f(x, y, _v[1].z()) - _v[1];
auto v2_P = Vector3f(x, y, _v[2].z()) - _v[2];
auto v0pCross = v0_v1.cross(v0_P);
auto v1pCross = v1_v2.cross(v1_P);
auto v2pCross = v2_v0.cross(v2_P);
if (v0pCross.dot(v1pCross) >= 0 && v0pCross.dot(v2pCross) >= 0)
return true;
return false;
}
因为我们判断的是一个像素的中心点是否在三角形内部,所以需要给x,y 分别加0.5,即insideTriangle(x+0.5,y+0.5,t.v)
注意:Vector3f Triangle::v[3] 中存放的就是三角形的三个顶点。
3.根据插值得到的深度值和深度缓冲的深度值比较。
插值运算使用代码框架,所以这块比较简单。
代码如下
for (int i = xMin; i <= xMax; i++)
{
for (int j = yMin; j <= yMax; j++)
{
if (insideTriangle(i+0.5f, j+0.5f,t.v))
{
auto[alpha, beta, gamma] = computeBarycentric2D(i, j, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int index = get_index(i, j);
if (depth_buf[index] > z_interpolated)
{
depth_buf[index] = z_interpolated; // 更新深度缓冲区
set_pixel(Vector3f(i,j,z_interpolated),t.getColor());
}
}
}
}
注意:如果当前z值小于深度缓冲区的深度值,一定要更新深度缓冲区。
结果
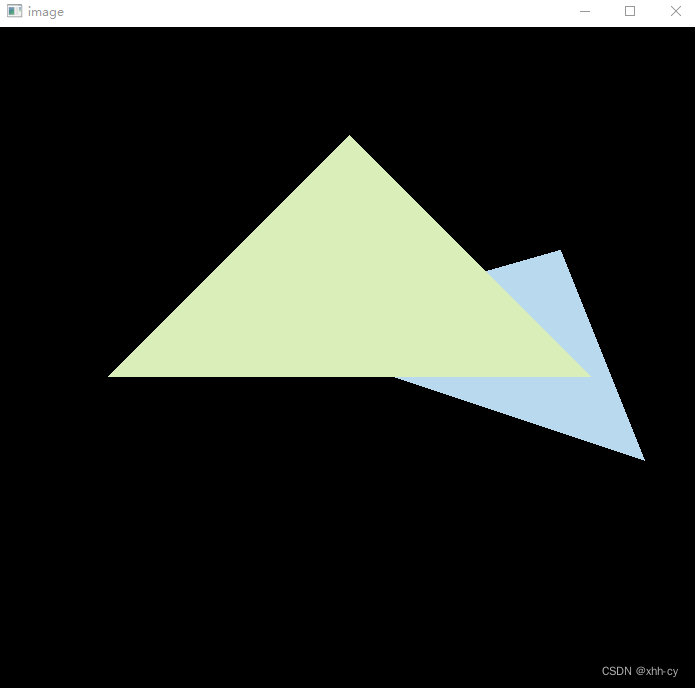
代码:
static bool insideTriangle(int x, int y, const Vector3f* _v)
{
// TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
auto v0_v1 = _v[1] - _v[0];
auto v1_v2 = _v[2] - _v[1];
auto v2_v0 = _v[0] - _v[2];
auto v0_P = Vector3f(x, y, _v[0].z()) - _v[0];
auto v1_P = Vector3f(x, y, _v[1].z()) - _v[1];
auto v2_P = Vector3f(x, y, _v[2].z()) - _v[2];
auto v0pCross = v0_v1.cross(v0_P);
auto v1pCross = v1_v2.cross(v1_P);
auto v2pCross = v2_v0.cross(v2_P);
if (v0pCross.dot(v1pCross) >= 0 && v0pCross.dot(v2pCross) >= 0)
return true;
return false;
}
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
int xMin, yMin, xMax, yMax;
xMin = std::floor(std::min(std::min(v[0].x(),v[1].x()),v[2].x()));
yMin = std::floor(std::min(std::min(v[0].y(), v[1].y()), v[2].y()));
xMax = std::ceil(std::max(std::max(v[0].x(), v[1].x()), v[2].x()));
yMax = std::ceil(std::max(std::max(v[0].y(), v[1].y()), v[2].y()));
for (int i = xMin; i <= xMax; i++)
{
for (int j = yMin; j <= yMax; j++)
{
if (insideTriangle(i+0.5f, j+0.5f,t.v))
{
auto[alpha, beta, gamma] = computeBarycentric2D(i, j, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
int index = get_index(i, j);
if (depth_buf[index] > z_interpolated)
{
depth_buf[index] = z_interpolated;
set_pixel(Vector3f(i,j, z_interpolated),t.getColor());
}
}
}
}
}
参考文献
判断点是否在三角形内