【算法训练-二叉树 一】【遍历二叉树】前序遍历、中序遍历、后续遍历、层序遍历、锯齿形层序遍历、二叉树右视图

news2024/12/23 20:35:59

废话不多说，喊一句号子鼓励自己：程序员永不失业，程序员走向架构！本篇Blog的主题是【二叉树的遍历】，使用【二叉树】这个基本的数据结构来实现，这个高频题的站点是：CodeTop，筛选条件为：目标公司+最近一年+出现频率排序，由高到低的去牛客TOP101去找，只有两个地方都出现过才做这道题（CodeTop本身汇聚了LeetCode的来源），确保刷的题都是高频要面试考的题。

在这里插入图片描述
就着这两个高频题目把二叉树的遍历类型题目刷一遍
在这里插入图片描述

名曲目标题后，附上题目链接，后期可以依据解题思路反复快速练习，题目按照题干的基本数据结构分类，且每个分类的第一篇必定是对基础数据结构的介绍。

二叉树的前序遍历【EASY】

前序、中序、后序都有迭代和递归的实现方式

题干

直接粘题干和用例

解题思路

前序遍历简单来说就是“根左右”，展开来说就是对于一颗二叉树优先访问其根节点，然后访问它的左子树，等左子树全部访问完了再访问其右子树，而对于子树也按照之前的访问方式，直到到达叶子节点，每次访问一个节点之后，它的左子树是一个要前序遍历的子问题，它的右子树同样是一个要前序遍历的子问题。那我们可以用递归处理：

  • 终止条件： 当子问题到达叶子节点后，后一个不管左右都是空，因此遇到空节点就返回。
  • 返回值： 每次处理完子问题后，就是将子问题访问过的元素返回，依次存入了数组中。
  • 本级任务： 每个子问题优先访问这棵子树的根节点，然后递归进入左子树和右子树。

具体做法：
step 1：准备数组用来记录遍历到的节点值，Java可以用List
step 2：从根节点开始进入递归，遇到空节点就返回，否则将该节点值加入数组。
step 3：依次进入左右子树进行递归。

代码实现

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：无
算法：递归、DFS
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] preorderTraversal (TreeNode root) {
        // 1 定义用来返回的数据
        List<Integer> list = new ArrayList<>();
        // 2 递归填充list的值
        preorder(list, root);
        // 3 返回结果处理
        int[] result = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            result[i] = list.get(i);
        }
        return result;
    }

    private void preorder(List<Integer> list, TreeNode root) {
        // 1 递归终止条件
        if (root == null) {
            return;
        }
        // 2 按顺序递归填充左右子树
        list.add(root.val);
        preorder(list, root.left);
        preorder(list, root.right);
    }
}

复杂度分析

时间复杂度：遍历了N个节点，所以时间复杂度为O（N）
空间复杂度：最坏情况下，树退化为链表，递归栈深度为N，所以空间复杂度为O（N）

二叉树的中序遍历【EASY】

换位中序遍历

题干

直接粘题干和用例

解题思路

如果一棵二叉树，对于每个根节点都优先访问左子树，那结果是什么？从根节点开始不断往左，第一个被访问的肯定是最左边的节点。然后访问该节点的右子树，最后向上回到父问题。因为每次访问最左的元素不止对一整棵二叉树成立，而是对所有子问题都成立，因此循环的时候自然最开始都是遍历到最左，然后访问，然后再进入右子树，我们可以用栈来实现回归父问题

  1. 寻找最左子树，此过程逐层将树及左子树的根节点压入栈中，把要后处理的上层子树根节点先压入操作栈
  2. 栈顶即当前最左子树根节点，也是上层子树的左子节点，将值放入到list
  3. 节点指针移动到当前指针右节点，如果右节点为空，则本层处理完成，栈再弹出上层节点，接着循环处理

其实思路与递归就相似了，只不过将递归栈具象化了

代码实现

递归的思路和代码不再赘述，直接给出

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] inorderTraversal (TreeNode root) {
        // 1 定义入参和返回值
        List<Integer> list = new ArrayList<>();
        // 2 中序递归获取list
        inorder(list, root);
        // 3 list结果转换
        int[] result = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            result[i] = list.get(i);
        }
        return result;
    }

    private void inorder(List<Integer> list, TreeNode root) {
        // 1 终止条件
        if (root == null) {
            return;
        }

        inorder(list, root.left);
        list.add(root.val);
        inorder(list, root.right);
    }
}

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：栈、DFS
算法：迭代
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] inorderTraversal (TreeNode root) {
        // 1 定义入参和辅助栈
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<TreeNode>();
        if (root == null) {
            return new int[0];
        }
        // 2 寻找最左子树
        TreeNode tempRoot = root;
        while (tempRoot != null || !stack.isEmpty()) {
            // 2-1 寻找最左子树，此过程逐层将树及左子树的根节点压入栈中
            while (tempRoot != null) {
                // 把要后处理的上层子树根节点先压入操作栈
                stack.push(tempRoot);
                tempRoot = tempRoot.left;
            }
            // 2-2 栈顶即当前最左子树根节点，也是上层子树的左子节点
            TreeNode node = stack.pop();
            list.add(node.val);
            // 2-3 节点指针移动到当前指针右节点，如果右节点为空，则本层处理完成，栈再弹出上层节点
            tempRoot = node.right;
        }
        // 3 list结果转换
        int[] result = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            result[i] = list.get(i);
        }
        return result;
    }
}

复杂度分析

时间复杂度：遍历了N个节点，所以时间复杂度为O（N）
空间复杂度：最坏情况下，树退化为链表，辅助递归栈深度为N，所以空间复杂度为O（N）

二叉树的后序遍历【EASY】

ok，再来看二叉树的后序遍历

题干

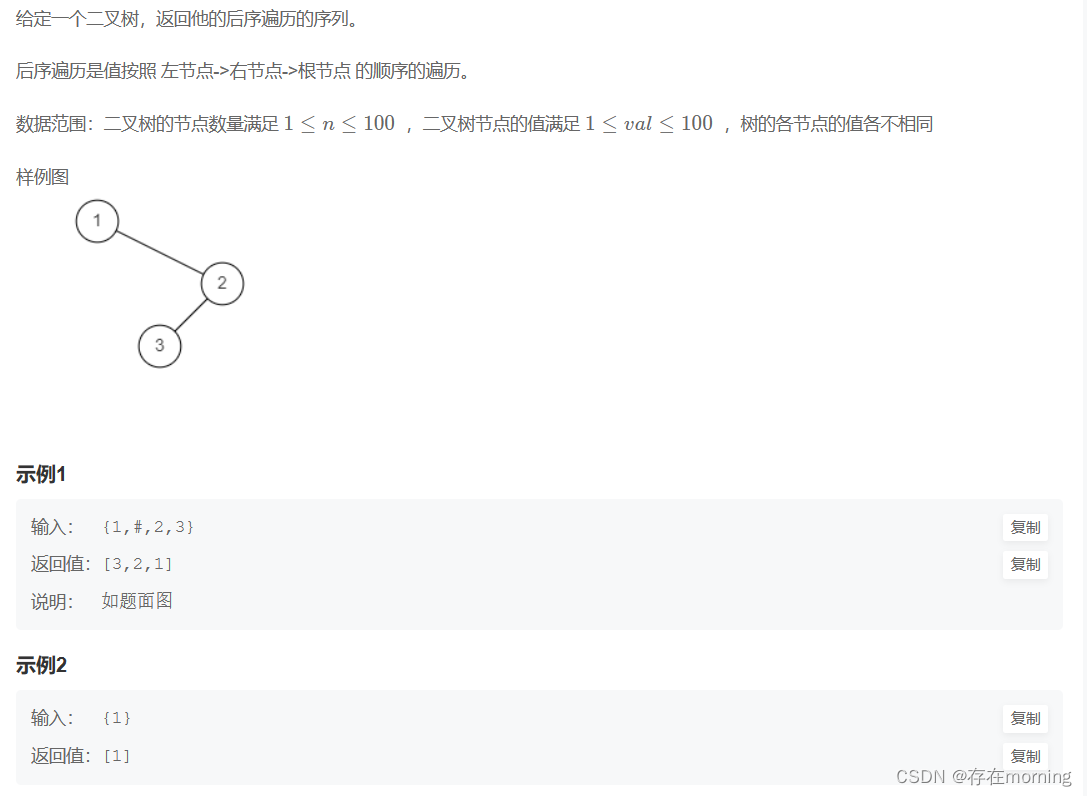
直接粘题干和用例

解题思路

左右根，同前序遍历及中序遍历的递归解法，不再赘述

代码实现

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：无
算法：递归、DFS
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] postorderTraversal (TreeNode root) {
        // 1 定义用来返回的数据
        List<Integer> list = new ArrayList<>();
        // 2 递归填充list的值
        postorder(list, root);
        // 3 返回结果处理
        int[] result = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            result[i] = list.get(i);
        }
        return result;
    }

    private void postorder(List<Integer> list, TreeNode root) {
        if (root == null) {
            return;
        }
        postorder(list, root.left);
        postorder(list, root.right);
        list.add(root.val);

    }
}

复杂度分析

时间复杂度：遍历了N个节点，所以时间复杂度为O（N）
空间复杂度：最坏情况下，树退化为链表，递归栈深度为N，所以空间复杂度为O（N）

二叉树的层序遍历【MID】

二叉树的层序遍历

题干

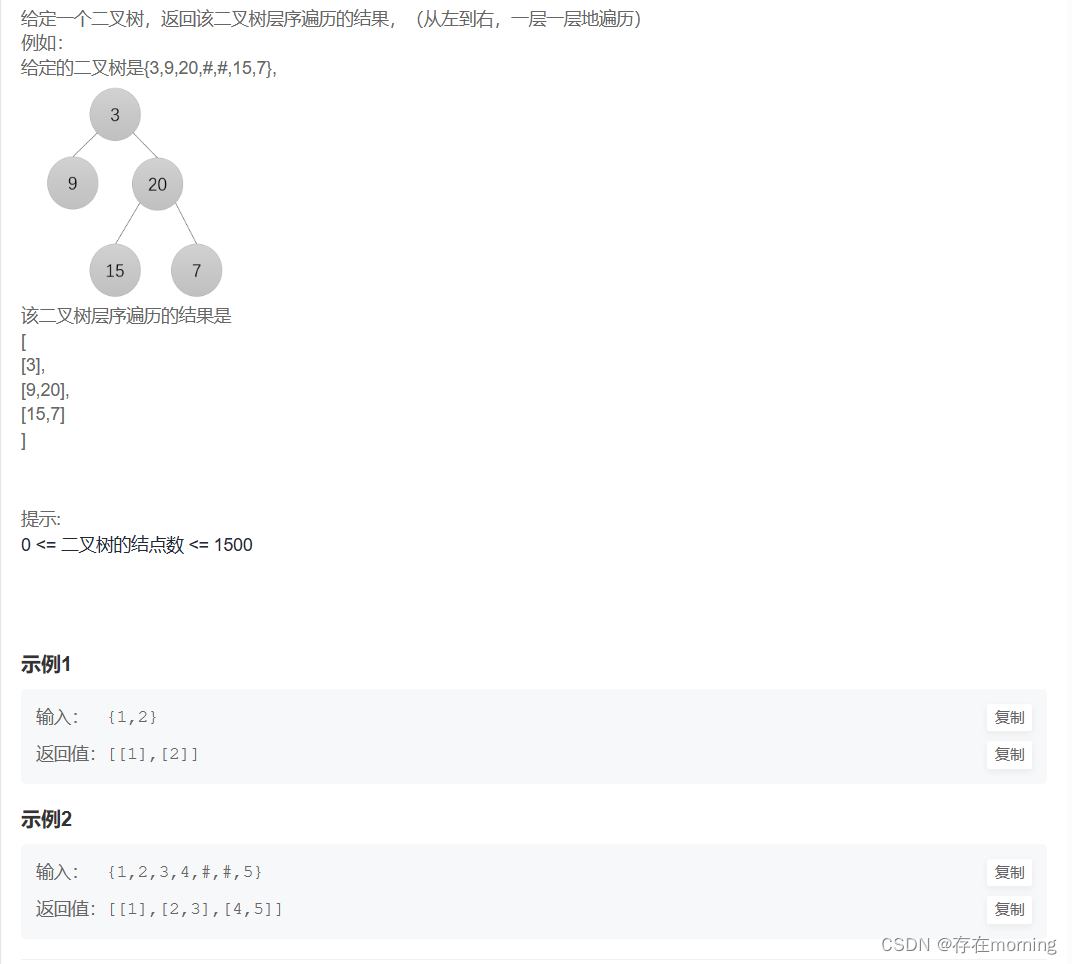
直接粘题干和用例

解题思路

二叉树的层次遍历就是按照从上到下每行，然后每行中从左到右依次遍历，得到的二叉树的元素值。对于层次遍历，我们通常会使用队列来辅助：

因为队列是一种先进先出的数据结构，我们依照它的性质，如果从左到右访问完一行节点，并在访问的时候依次把它们的子节点加入队列，那么它们的子节点也是从左到右的次序，且排在本行节点的后面，因此队列中出现的顺序正好也是从左到右，正好符合层次遍历的特点

  • step 1：首先判断二叉树是否为空，空树没有遍历结果。
  • step 2：建立辅助队列，根节点首先进入队列。不管层次怎么访问，根节点一定是第一个，那它肯定排在队伍的最前面。
  • step 3：每次进入一层，统计队列中元素的个数。因为每当访问完一层，下一层作为这一层的子节点，一定都加入队列，而再下一层还没有加入，因此此时队列中的元素个数就是这一层的元素个数。
  • step 4：每次遍历一层的节点数，将其依次从队列中弹出，然后加入这一行的一维数组中，如果它们有子节点，依次加入队列排队等待访问。
  • step 5：访问完这一层的元素后，将这个一维数组加入二维数组中，再访问下一层。

在这里插入图片描述

代码实现

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：队列
算法：迭代、BFS
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
        // 1 定义要返回的数据结构
        ArrayList<ArrayList<Integer>> result = new ArrayList<>();
        // 2 定义辅助队列结构，每次队列都只存一层
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        // 3 首先将第一层也就是根节点放入队列
        if (root == null) {
            return new ArrayList<>();
        }
        queue.add(root);

        // 4 核心处理逻辑，分层获取元素并加入列表
        while (!queue.isEmpty()) {
            ArrayList<Integer> levelList = new ArrayList<Integer>();
            // 需要用一个临时变量承接队列大小，否则每次新加一层永远无法遍历完本层
            int queueSize = queue.size();
            for (int i = 0; i < queueSize; i++) {
                // 4-1 获取队首元素，当前层元素，并添加到层列表中
                TreeNode node = queue.poll();
                levelList.add(node.val);
                // 4-2 分别将节点左右元素添加到队列尾部
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            // 4-3 将本层元素集合添加到结果集中
            result.add(levelList);
        }
        return result;
    }
}

复杂度分析

时间复杂度：遍历了一遍树，时间复杂度为O（N）
空间复杂度：使用了辅助队列，空间复杂度为O（N）

二叉树的锯齿形层序遍历【MID】

难度升级，每层要反过来

题干

直接粘题干和用例

解题思路

解题思路与层次遍历相同，只不过需要隔行反转。只需增加标志位即可。

代码实现

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：队列
算法：迭代、BFS
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pRoot TreeNode类
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> Print (TreeNode pRoot) {
        // 1 定义返回结果
        ArrayList<ArrayList<Integer>> result = new ArrayList<>();
        if (pRoot == null) {
            return new ArrayList<>();
        }
        // 2 定义队列，并将根节点放入
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(pRoot);
        // 3 设置反转标志位，隔行反转
        boolean isReverse = false;
        // 4 核心逻辑，将数据放入结果集
        while (!queue.isEmpty()) {
            int queueSize = queue.size();
            ArrayList<Integer> levelList = new ArrayList<Integer>();
            for (int i = 0; i < queueSize; i++ ) {
                TreeNode node = queue.poll();
                levelList.add(node.val);
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
            }
            // 依据标志位结果进行层级数据反转
            if (isReverse) {
                Collections.reverse(levelList);
            }
            // 重置标志位，以便下一层反转
            isReverse = !isReverse;
            result.add(levelList);
        }

        return result;
    }
}

复杂度分析

时间复杂度：遍历了一遍树，时间复杂度为O（N）
空间复杂度：使用了辅助队列，空间复杂度为O（N）

二叉树的右视图【MID】

使用深度优先搜素方法

题干

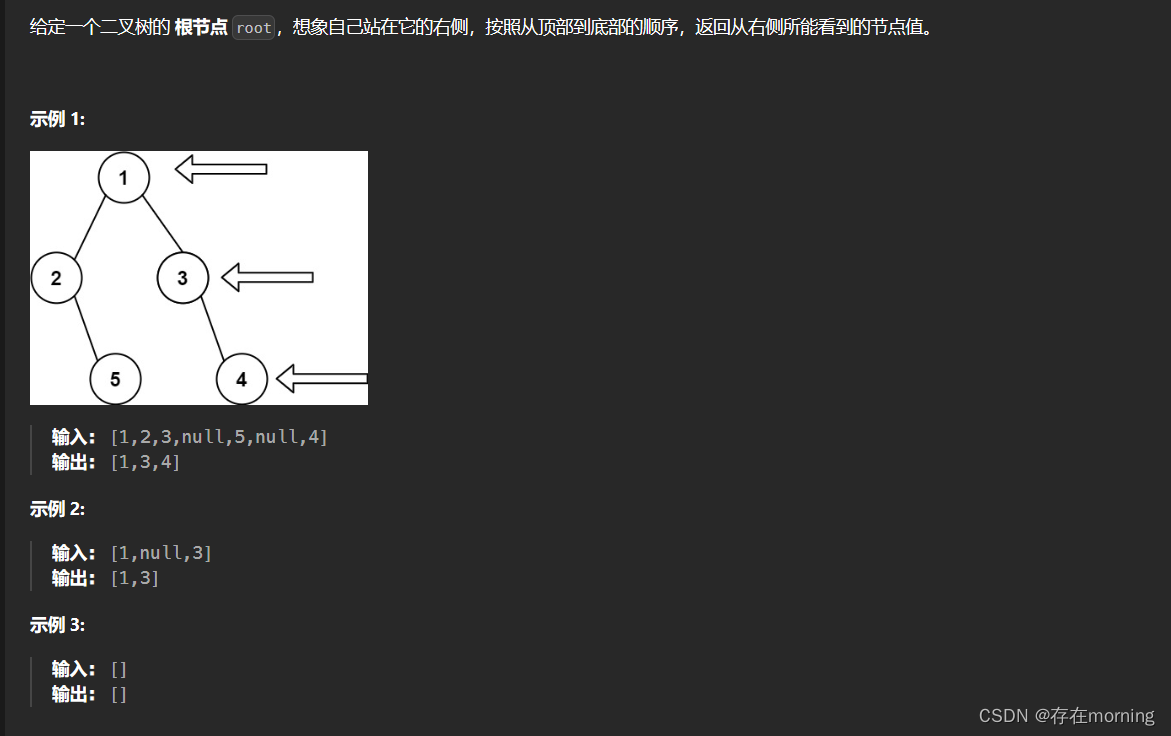
直接粘题干和用例

解题思路

我们可以对二叉树进行层次遍历，那么对于每层来说，最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。

  • 执行广度优先搜索，左结点排在右结点之前，这样，我们对每一层都从左到右访问。因此，只保留每个深度最后访问的结点，我们就可以在遍历完整棵树后得到每个深度最右的结点
    在这里插入图片描述
    所以只要按照层序遍历的思路，把每一层的最后一个节点放到结果集就行了。

代码实现

给出代码实现基本档案

基本数据结构：二叉树
辅助数据结构：队列
算法：迭代、BFS
技巧：无

其中数据结构、算法和技巧分别来自：

  • 10 个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
  • 10 个算法：递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
  • 技巧：双指针、滑动窗口、中心扩散

当然包括但不限于以上

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 求二叉树的右视图
     * @param root 树的根节点
     * @param inOrder int整型一维数组 中序遍历
     * @return int整型一维数组
     */
    public List<Integer> rightSideView(TreeNode root) {
        // 1 定义返回的结果集
        List<Integer> result = new ArrayList<Integer>();
        if (root == null) {
            return new ArrayList<Integer>();
        }
        // 2 定义队列，用来容纳每一层节点
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(root);
        // 3 遍历每一层并获取最右边的节点
        while (!queue.isEmpty()) {
            int queueSize = queue.size();
            for (int i = 0; i < queueSize; i++) {
                TreeNode node = queue.poll();
                if (node.left != null) {
                    queue.add(node.left);
                }
                if (node.right != null) {
                    queue.add(node.right);
                }
                // 如果节点是本层最后一个节点，则添加到结果集中
                if (i == queueSize - 1) {
                    result.add(node.val);
                }
            }
        }
        return result;

    }


}

复杂度分析

时间复杂度： O(N)，每个节点都入队出队了 1 次。
空间复杂度： O(N)，使用了额外的队列空间。

拓展知识：深度优先遍历和广度优先遍历

广度优先搜索（BFS）和深度优先搜索（DFS）是两种经典的图遍历算法，它们也可以用于二叉树的遍历和搜索。以下是它们的定义以及在二叉树中的应用场景：

广度优先搜索（BFS）：

BFS是一种图遍历算法，它从一个起始节点开始，逐层地遍历与该节点相邻的节点，然后再遍历与这些相邻节点相邻的节点，以此类推。BFS通常使用队列数据结构来实现。

在二叉树中的应用场景：

  1. 层级遍历：BFS可以用于按层级遍历二叉树，从根节点开始，逐层遍历，可以方便地实现层级顺序的操作。
  2. 查找最小深度：BFS可以用于查找二叉树的最小深度，即从根节点到最近叶子节点的最短路径。
  3. 查找特定元素：如果您需要在二叉树中查找特定元素，BFS可以用于在树中搜索，一旦找到目标元素，就可以停止搜索。
  4. 判断是否为完全二叉树：BFS可以用于判断二叉树是否是完全二叉树，通过观察层级遍历的结果，可以检查每一层是否都填满节点。

深度优先搜索（DFS）：

DFS是一种图遍历算法，它从一个起始节点开始，沿着一条路径一直深入到无法继续前进的节点，然后返回上一层，继续探索其他路径。DFS通常使用递归函数或显式的栈数据结构来实现。

在二叉树中的应用场景：

  1. 前序遍历：DFS通常用于前序遍历二叉树，即先访问根节点，然后递归地访问左子树和右子树。前序遍历用于深度优先搜索问题。
  2. 中序遍历：DFS也可以用于中序遍历二叉树，即先递归地访问左子树，然后访问根节点，最后递归地访问右子树。中序遍历在二叉搜索树中用于获取有序元素。
  3. 后序遍历：DFS还可用于后序遍历二叉树，即先递归地访问左子树和右子树，最后访问根节点。后序遍历在某些问题中很有用，例如计算表达式的值或查找树的高度。

总的来说，BFS适用于需要层级遍历或查找最短路径的问题，而DFS适用于需要深度优先搜索或对树的结构进行更复杂操作的问题。在二叉树中，您可以根据具体问题的要求选择使用BFS或DFS。有时，问题可能需要同时使用这两种方法以解决不同的子问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1018146.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何实现一个IO口读取多个设备信息

如何实现一个IO口读取多个设备信息

前言 &#xff08;1&#xff09;今天遇到一个有意思的问题一个IO口如何读取多个电机的堵转问题。之后他就发了一张图片 &#xff08;2&#xff09;看到这个问题&#xff0c;之前先说一个简单的。我们如何实现一个IO读取多个按键&#xff0c;了解了这个之后&#xff0c;对于多个…
阅读更多...
Python 变量

Python 变量

视频版教程 Python3零基础7天入门实战视频教程 变量 无论使用什么语言编程&#xff0c;总要处理数据&#xff0c;处理数据就需要使用变量来保存数据。变量就像一个个小容器&#xff0c;用于“盛装”程序中的数据。 再说说&#xff0c;Python的数据类型&#xff0c;有以下六种…
阅读更多...
Prometheus+Grafana 基础监控告警体系搭建（一）：服务的基本安装

Prometheus+Grafana 基础监控告警体系搭建（一）：服务的基本安装

文章目录 1. prometheus 安装1.1. 下载安装包1.2. 基本设置1.3. 解压安装包1.4. 配置 service 启动文件1.5. 启动服务 2. Grafana 安装2.1. 下载安装包2.2. 安装2.3. 启动服务 3. 总结一下 打算重新练下手&#xff0c;免得忘记了&#xff0c;这次内网进行了全面部署演示&#x…
阅读更多...
编程任务|随机摆放的刀叉开始认识数学思维

编程任务|随机摆放的刀叉开始认识数学思维

任务源自旧版的Brilliant数学讨论问题。2019-09-02我曾经发布过&#xff0c;可惜已经下线&#xff0c;幸活大喵做足备份。 该问题看似是概率问题&#xff0c;实则不然。 官方给出的解法透露出一个非常重要的数学思维方法&#xff1a; 数学语言 —— 为何以及如何构造一个函数 f…
阅读更多...
计算机丢失msvcr110.dll解决办法，多种msvcr110.dll解决方法分享

计算机丢失msvcr110.dll解决办法，多种msvcr110.dll解决方法分享

随着 Windows 操作系统的发展&#xff0c;越来越多的用户在使用电脑时遇到了计算机丢失 msvcr110.dll 的问题。msvcr110.dll 是 Windows 操作系统中的一个动态链接库文件&#xff0c;它包含了许多常用的 C 运行库函数。因此&#xff0c;当计算机丢失 msvcr110.dll 时&#xff0…
阅读更多...
Kotlin File useLines nameWithoutExtension extension

Kotlin File useLines nameWithoutExtension extension

Kotlin File useLines nameWithoutExtension extension import java.io.Filefun main(args: Array<String>) {val filePath "myfile.txt"val file File(filePath)println(file.name) //文件名字&#xff0c;不包括路径println(file.isFile) //是文件吗pri…
阅读更多...
PTA：7-4 顺序表（删除）

PTA：7-4 顺序表（删除）

顺序表&#xff08;删除&#xff09; 题目输入样例输出样例 代码 题目 输入样例 10 55 11 9 15 67 12 18 33 6 22 10 20输出样例 55 9 67 33 6 22代码 #include<iostream> using namespace std; void deletes(int* arr, int& sz, int left, int right) {int newId…
阅读更多...
Vue入门简介（带你打开Vue的大门）

Vue入门简介（带你打开Vue的大门）

目录 前言 一、Vue简介 1. 什么是Vue 2. Vue的应用场景 3. Vue的作用&#xff08;重要性&#xff09; 4. 什么是MVVM模式 5. 开源库网址 二、Vue入门使用 1. 基础使用步骤 1.1 引入Vue.js 1.2 创建Vue实例 1.3 编写Vue模板 1.4 数据绑定与指令 1.5 调用Vue方法和…
阅读更多...
【C++】哈希位图和布隆过滤器

【C++】哈希位图和布隆过滤器

哈希位图优缺点位图应用模拟实现代码 哈希布隆过滤器哈希布隆过滤器的提出哈希布隆过滤器概念模拟实现代码 为什么哈希布隆图要比位图省空间 哈希位图和布隆过滤器都是常用的概率数据结构&#xff0c;用于高效地判断一个元素是否存在于一个集合当中&#xff0c;但它们在实现方法…
阅读更多...
The driver has not received any packets from the server

The driver has not received any packets from the server

在测试数据迁移时遇到的错误。 目录 一、错误 二、解决 三、数据迁移测试 3.1 环境 3.2 源码及测试 3.2.1 源码 3.2.2 测试结果&#xff08;太慢&#xff09; 3.2.3 源码修改 3.2.4 异常及解决 一、错误 The driver has not received any packets from the server. 二…
阅读更多...
关于软件测试的方法详解，你知道多少呢？

关于软件测试的方法详解，你知道多少呢？

一、 软件测试方法 1. 软件测试方法包括&#xff1a;白盒测试(White Box Testing)、黑盒测试(Black Box Testing)、灰盒测试、静态测试、动态测试。 2. 白盒测试&#xff1a;是一种测试用例设计方法&#xff0c;在这里盒子指的是被测试的软件&#xff0c;白盒&#xff0c;顾名…
阅读更多...
想要精通算法和SQL的成长之路 - 最长回文子序列

想要精通算法和SQL的成长之路 - 最长回文子序列

想要精通算法和SQL的成长之路 - 最长回文子序列 前言一. 最长回文子序列 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 最长回文子序列 原题链接 首先&#xff0c;我们看下动态规划方程的定义&#xff0c;我们用dp[i][j] 来代表&#xff1a;字符串s在下标区间为[i,j]之间…
阅读更多...
Java“牵手”lazada商品列表页数据采集+lazada商品价格数据排序，lazadaAPI接口申请指南

Java“牵手”lazada商品列表页数据采集+lazada商品价格数据排序，lazadaAPI接口申请指南

Lazada是东南亚首屈一指的网上购物平台&#xff0c;中文名为来赞达&#xff0c;拥有较多的品牌和销售商。2016年&#xff0c;Lazada成为阿里巴巴集团的区域旗舰&#xff0c;并得到了阿里巴巴一流的技术基础设施的支持。 Lazada来赞达在2012年成立&#xff0c;总部设在新加坡&a…
阅读更多...
JavaScript基础知识11——运算符:赋值运算符

JavaScript基础知识11——运算符:赋值运算符

哈喽&#xff0c;大家好&#xff0c;我是雷工&#xff01; 今天公乌素这缺水的镇子&#xff0c;稀稀拉拉下了一天的雨&#xff0c;一场秋雨一场寒&#xff0c;风开始愈发清凉。 看日历发现明天就是二十四节气里的白露了&#xff0c;都白露了&#xff0c;原来不知不觉已经深秋了…
阅读更多...
笔记（五）-传统图机器学习的特征工程-全图

笔记（五）-传统图机器学习的特征工程-全图

1、引言 -提取出的特征要能够反应全图结构特点 2、全图信息种类 Bag-of-Nodes Bag-of-Nodes degrees -就是找同分异构体 -和节点特征的子图不同的是 可以存在孤立结点计算全图的子图个数&#xff0c;而不是特定邻域的子图个数 Graphlet kernel -两个图作数量积&#xff0c;…
阅读更多...
Unity 安装及运行MLAgents

Unity 安装及运行MLAgents

1、下载ML-Agents 下载地址 GitHub - Unity-Technologies/ml-agents: The Unity Machine Learning Agents Toolkit (ML-Agents) is an open-source project that enables games and simulations to serve as environments for training intelligent agents using deep reinfo…
阅读更多...
如何修复丢失的vcruntime140_1.dll文件

如何修复丢失的vcruntime140_1.dll文件

在编程中&#xff0c;我们经常会遇到各种问题和挑战。其中之一就是缺少必要的运行库文件&#xff0c;如vcruntime140_1.dll&#xff0c;这可能会导致我们的程序无法正常运行。本文将详细介绍6种解决此问题的方法&#xff0c;并详细讲解vcruntime140_1.dll文件的作用。 vcruntim…
阅读更多...
企业级SpringBoot单体项目模板 —— 全局配置

企业级SpringBoot单体项目模板 —— 全局配置

&#x1f61c;作 者&#xff1a;是江迪呀✒️本文关键词&#xff1a;SpringBoot、模版、企业级☀️每日 一言&#xff1a;你坚持下来了&#xff0c;而别人坚持不下来&#xff0c;这就是你的资本。 文章目录 一、全局异常配置1.1 全局异常处理1.2 处理业务异常类1.3…
阅读更多...
并查集 size 的优化

并查集 size 的优化

我们把如下图所示的并查集&#xff0c;进行 union(4,9) 操作。 合并操作后的结构为&#xff1a; 可以发现&#xff0c;这个结构的树的层相对较高&#xff0c;若此时元素数量增多&#xff0c;这样产生的消耗就会相对较大。解决这个问题其实很简单&#xff0c;在进行具体指向操作…
阅读更多...
【陕西理工大学-数学软件实训】数学实验报告（8）（数值微积分与方程数值求解）

【陕西理工大学-数学软件实训】数学实验报告（8）（数值微积分与方程数值求解）

目录 一、实验目的 二、实验要求 三、实验内容与结果 四、实验心得 一、实验目的 1. 掌握求数值导数和数值积分的方法。 2. 掌握代数方程数值求解的方法。 3. 掌握常微分方程数值求解的方法。 二、实验要求 1. 根据实验内容&#xff0c;编写相应的MATLAB程序&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023