文章目录
- 一.树的专业术语
- 二.二叉树的原理
- 三.常见的二叉树分类
- 1.完全二叉树
- 2.平衡二叉树
- 3.二叉搜索树
- 四.二叉搜索树算法具体实现
- 五.二叉搜索树具体实现代码
一.树的专业术语
首先先介绍树的专业术语

二.二叉树的原理
二叉搜索树(Binary Search Tree,BST)是一种常见的数据结构,它在计算机科学中被广泛应用于数据的存储和检索。它是一棵二叉树,其中每个节点都包含一个键值,并满足以下性质:
左子树中的所有节点的键值小于根节点的键值。
右子树中的所有节点的键值大于根节点的键值。
左子树和右子树也都是二叉搜索树。
这个性质使得二叉搜索树具有非常高效的查找、插入和删除操作。
二叉搜索树的原理可以通过以下几个操作来解释:
查找(Search):从根节点开始,比较要查找的键值与当前节点的键值。如果它等于当前节点的键值,则查找成功。如果要查找的键值小于当前节点的键值,则继续在左子树中查找;如果要查找的键值大于当前节点的键值,则继续在右子树中查找。直到找到匹配的键值或者遍历到叶子节点为止。
插入(Insertion):插入操作从根节点开始,比较要插入的键值与当前节点的键值。如果要插入的键值小于当前节点的键值,并且当前节点没有左子节点,则将新节点作为当前节点的左子节点;如果要插入的键值大于当前节点的键值,并且当前节点没有右子节点,则将新节点作为当前节点的右子节点。如果当前节点已有左子节点或右子节点,则继续在相应的子树上进行插入操作,直到找到合适的位置。
删除(Deletion):删除操作是比较复杂的,因为需要考虑不同的情况。首先,找到要删除的节点。如果要删除的节点没有子节点,可以直接删除它。如果要删除的节点只有一个子节点,可以用其子节点替换它。如果要删除的节点有两个子节点,可以找到其右子树中的最小节点(或者左子树中的最大节点)来替换它。替换后,再删除该最小(或最大)节点。删除操作需要保持二叉搜索树的性质。
总结来说,二叉搜索树通过利用节点键值的大小关系,将较小的值放在左子树,较大的值放在右子树。这样的组织结构可以在平均情况下以O(log n)的时间复杂度进行查找、插入和删除操作,但在最坏情况下,如果树的形状极度不平衡,时间复杂度可能会退化为O(n)。因此,在实际应用中,需要进行平衡操作,如红黑树或AVL树,以保证树的平衡性,提高性能。
三.常见的二叉树分类
1.完全二叉树
完全二叉树 — 若设二叉树的高度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数第 h 层有叶子节点,并且叶子结点都是从左到右依次排布,这就是完全二叉树(堆就是完全二叉树)。
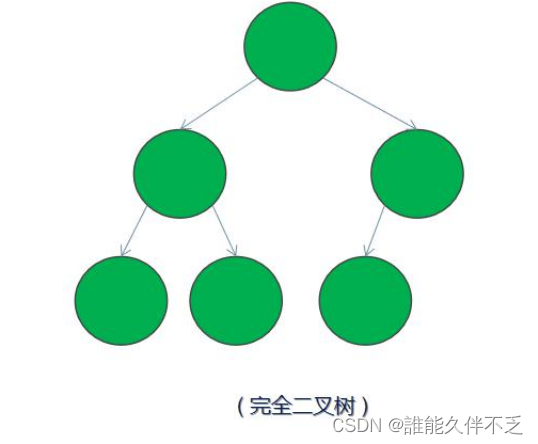

2.平衡二叉树
平衡二叉树— 又被称为 AVL 树,它是一颗空树或左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
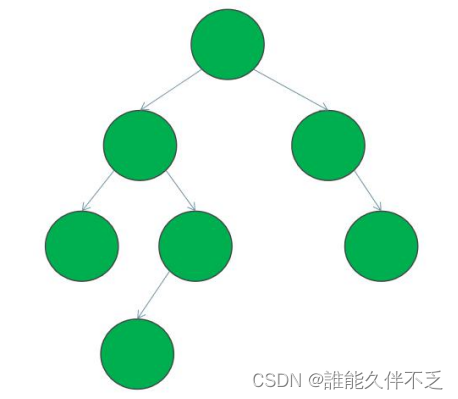
3.二叉搜索树
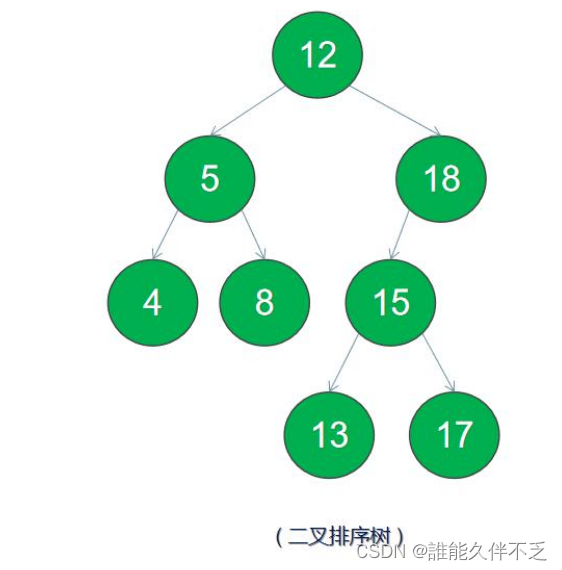
二叉搜索树 — 又称二叉查找树、二叉排序树(Binary Sort Tree)。它是一颗空树或是满足下列性质的二叉树:
1.若左子树不空,则左子树上所有节点的值均小于或等于它的根节点的值;
2.若右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
3.左、右子树也分别为二叉排序树。
四.二叉搜索树算法具体实现
当我们在数组中查找一个数的时候,需要从前往后逐个遍历,这样效率很忙
二叉搜索树就是把数据用它的规则进行从大到小排序,使用折半查找(二分查找)
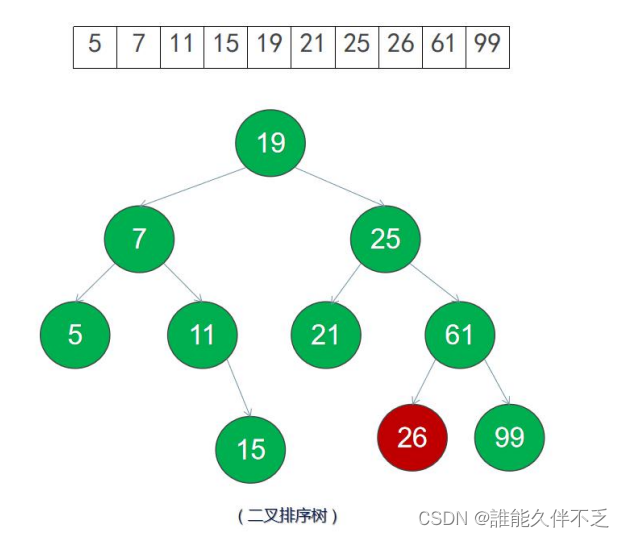
二叉树一般采用链式存储方式:每个结点包含两个指针域,指向两个孩子结点,还包含一个数据域,存储结点信息。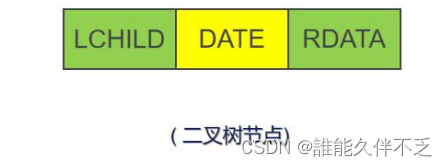
二叉搜索树插入节点
将要插入的结点 e,与节点 root 节点进行比较,若小于则去到左子树进行比较,若大于则去到右子树进行比较,重复以上
操作直到找到一个空位置用于放置该新节点
二叉搜索树删除节点
将要删除的节点的值,与节点 root 节点进行比较,若小于则去到左子树进行比较,若大于则去到右子树进行比较,重复以
上操作直到找到一个节点的值等于删除的值,则将此节点删除。删除时有 4 中情况须分别处理:
1.删除节点不存在左右子节点,即为叶子节点,直接删除
2.删除节点存在左子节点,不存在右子节点,直接把左子节点替代删除节点
3.删除节点存在右子节点,不存在左子节点,直接把右子节点替代删除节点
4.删除节点存在左右子节点,则取左子树上的最大节点或右子树上的最小节点替换删除节点。
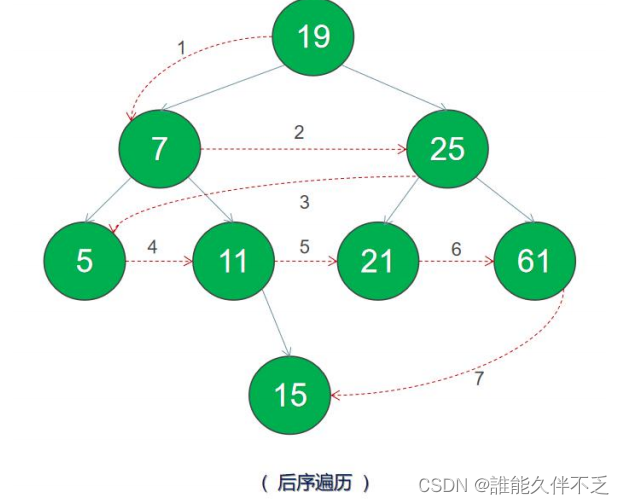
二叉树的遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问所有结点,使得每个结点被当且访问一次。共分为四种方式:
前序遍历 - 先访问根节点,然后前序遍历左子树,再前序遍历右子树
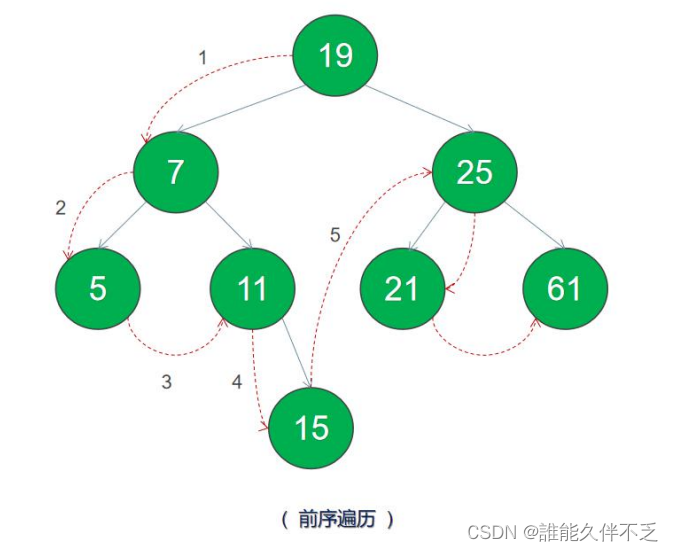
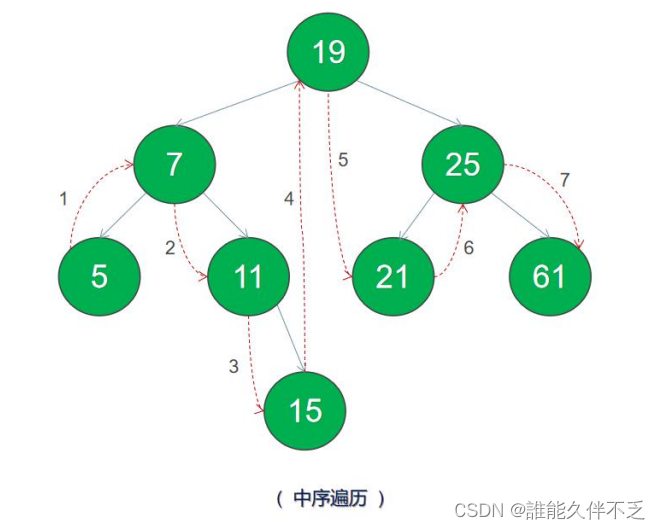
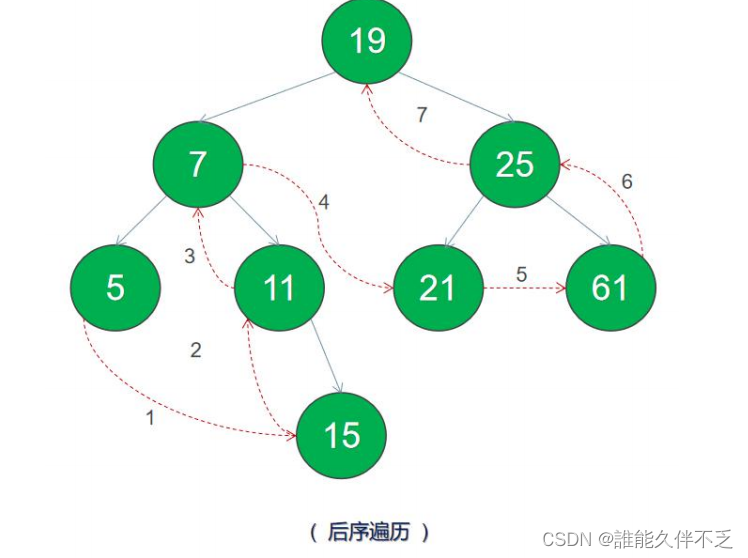
五.二叉搜索树具体实现代码
stack.h
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
#define MaxSize 128
typedef struct _SqStack {
Bnode* base; //栈底指针
Bnode* top; //栈顶指针
}SqStack;
bool InitStack(SqStack& S) //构造一个空栈 S
{
S.base = new Bnode[MaxSize];//为顺序栈分配一个最大容量为 Maxsize 的空间
if (!S.base) return false; //空间分配失败
S.top = S.base; //top 初始为 base,空栈
return true;
}
bool PushStack(SqStack& S, Bnode e) { 插入元素 e 为新的栈顶元素
if (S.top - S.base == MaxSize) {
printf("栈为满!\n");
return false;
}
*(S.top++) = e; //元素 e 压入栈顶,然后栈顶指针加 1,等价于*S.top=e;S.top++;
return true;
}
bool PopStack(SqStack& S, Bnode& e) { //删除 S 的栈顶元素,暂存在变量 e中
if (S.top == S.base) {
printf("空栈!\n");
return false;
}
e = *(--S.top); //栈顶指针减 1,将栈顶元素赋给 e
return true;
}
Bnode* GetTop(SqStack& S) { //返回 S 的栈顶元素,栈顶指针不变
if (S.base != S.top) {
return S.top - 1;
}
else
{
printf("空栈!\n");
return nullptr;
}
}
int GetSize(SqStack& S) { //返回栈中元素个数
return (S.top - S.base);
}
bool IsEmpty(SqStack& S) {//判断栈是否为空
if (S.top == S.base) {
return true;
}
else {
return false;
}
}
void DestroyStack(SqStack& S) {//销毁栈
if (S.base) {
free(S.base);
S.base = NULL;
S.top = NULL;
}
}
tree.h
#pragma once
#define MAX_NODE 1024
#define isLess(a,b) (a<b)
#define isEqual(a,b) (a==b)
typedef int ElemType;
typedef struct _Bnode {
ElemType data; //数据
struct _Bnode* lchild, * rchild; //左右孩子节点
}Bnode, Btree; //Bnode是结构体的指针类型,*Btree是提前定义好了的指向结构体的指针
// *Btree等于提前创建了一个存储_Bnode类型的指针
main
#include <iostream>
#include <assert.h>
#include <Windows.h>
#include "tree.h"
#include "stack.h"
#define MAX_NODE 1024
using namespace std;
bool InsertBtree(Btree** root, Bnode* node) { //插入
Bnode* tmp = nullptr;
Bnode* parent = nullptr;
bool abs = false;
if (!node) return false;
else {
node->lchild = nullptr;
node->rchild = nullptr;
}
if (*root) { //存在根节点
tmp = *root;
}
else //不存在根节点
{
*root = node;
return true;
}
while (tmp != NULL)
{
parent = tmp; //保存父节点
printf("父节点:%d\n", parent->data);
if (isLess(node->data, tmp->data)) {
tmp = tmp->lchild;
abs = true; //
}
else {
tmp = tmp->rchild;
abs = false;
}
}
//if (isLess(node->data,parent->data))
if (abs) { //找到空位置后,进行插入
parent->lchild = node;
}
else
{
parent->rchild = node;
}
return true;
}
int findMax(Btree* root) {
assert(root != nullptr);
//方式一,使用递归
/*if (root->rchild) {
root = root->rchild;
}
return root->data;*/
//方式二,使用循环
while (root->rchild)
{
root = root->rchild;
}
return root->data;
}
Btree* DeleteNode(Btree* root, int key, Btree*& deleteNode) {
if (root == nullptr)return NULL; //没有找到删除的节点
if (root->data > key) {
root->lchild = DeleteNode(root->lchild, key, deleteNode);
return root;
}
else if (root->data < key) {
root->rchild = DeleteNode(root->rchild, key, deleteNode);
return root;
}
deleteNode = root;
//删除节点不存在左右子节点,即为叶子节点,直接删除
//所有删除功能待实现
if (root->lchild == nullptr && root->rchild == nullptr) return NULL;
//删除节点只存在右子节点,直接用右子节点取代删除节点
if (root->lchild == nullptr && root->rchild != nullptr)return root->rchild;
//删除节点只存在左子节点,直接用左子节点取代删除节点
if (root->lchild != NULL && root->rchild == NULL)return root->lchild;
//删除节点存在左右子节点,直接用左子节点最大值取代删除节点
//循环断点仔细看看这段代码
int val = findMax(root->lchild);
root->data = val; //赋值
root->lchild = DeleteNode(root->lchild, val, deleteNode); //用完了就要删掉
return root;
}
//使用递归查询节点
Bnode* queryByRec(Btree* root, ElemType e) {
if (root == nullptr || isEqual(root->data, e))
return root;
else if (isLess(e, root->data))
return queryByRec(root->lchild, e);
else
return queryByRec(root->rchild, e);
}
//使用非递归查询节点
Bnode* queryByLoop(Bnode* root, int e) {
while (root != nullptr && !isEqual(root->data, e))
{
if (isLess(root->data, e)) {
root = root->rchild;
}
else {
root = root->lchild;
}
}
return root;
}
//采用递归实现前序遍历
void PreOrderRec(Btree* root) {
if (root == nullptr)return;
printf("-%d-", root->data);
PreOrderRec(root->lchild);
PreOrderRec(root->rchild);
}
//采用非递归实现前序遍历
//借助栈实现前序遍历
void PreOrder(Btree* root) {
Bnode cur;
if (root == nullptr)return;
SqStack stack;
InitStack(stack);
PushStack(stack,*root); //头节点先入栈
while (!(IsEmpty(stack)))
{
PopStack(stack, cur); //要遍历的节点
printf("-%d-", cur.data);
if (cur.rchild != nullptr) {
PushStack(stack,*(cur.rchild)); //右子节点先入栈,后处理
}
if (cur.lchild!=nullptr) {
PushStack(stack, *(cur.lchild));//左子节点后入栈,接下来先处理
}
}
DestroyStack(stack);
}
int main(void) {
int test[] = { 19, 7, 25, 5, 11, 15, 21, 61 };
Bnode* root = NULL, * node = NULL;
Bnode* Delete = nullptr; //记录被删除的节点
node = new Bnode;
node->data = test[0];
InsertBtree(&root, node); //插入根节点
for (int i = 1; i < sizeof(test) / sizeof(test[0]); i++) {
node = new Bnode;
node->data = test[i];
if (InsertBtree(&root, node)) {
printf("节点 %d 插入成功\n", node->data);
}
else {
printf("节点 %d 插入失败\n", node->data);
}
}
Bnode* tmp = queryByRec(root, 25);
printf("搜索二叉搜索树,节点 25 %s\n", tmp ? "存在" : "不存在");
Bnode* tmp1 = queryByRec(root, 55);
printf("搜索二叉搜索树,节点 55 %s\n", tmp1 ? "存在" : "不存在");
cout << endl;
PreOrderRec(root);
cout << endl;
PreOrder(root);
cout << endl;
cout << "删除节点 25" << endl;
Bnode* del = DeleteNode(root, 25, Delete);
Bnode* tmp2 = queryByRec(root, 25);
delete Delete; //销毁内存
printf("搜索二叉搜索树,节点 25 %s\n", tmp2 ? "存在" : "不存在");
cout << endl;
PreOrderRec(root);
cout << endl;
PreOrder(root);
cout << endl;
system("pause");
return 0;
}