文章目录

二分查找
移除元素
有序数组的平方
长度最小的子数组
螺旋矩阵
螺旋矩阵II

二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

Python：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        i, j = 0, len(nums) - 1
        while i <= j:
            mid = (i + j) // 2
            if nums[mid] < target:
                i = mid + 1
            elif nums[mid] > target:
                j = mid - 1
            else:
                return mid
        return -1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        for i, num in enumerate(nums):
            if num == target:
                return i
        return -1

Go：

func search(nums []int, target int) int {
	i, j := 0, len(nums)-1
	for i <= j {
		mid := i + (j-i)/2
		if nums[mid] < target {
			i = mid + 1
		} else if nums[mid] > target {
			j = mid - 1

		} else {
			return mid
		}
	}
	return -1
}

func search(nums []int, target int) int {
	for i, v := range nums {
		if v == target {
			return i
		}
	}
	return -1
}

移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以**「引用」**方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

Python：

#双指针
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        slow = fast = 0
        size = len(nums)
        while fast < size:
            if nums[fast] != val:
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
        return slow

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        while val in nums:
            nums.remove(val)
        return len(nums)

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        for i in range(nums.count(val)):
            nums.remove(val)
        return len(nums)

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        k=0
        for i in nums:
            if i != val:
                nums[k]=i
                k+=1
        return k

Go：

//双指针
func removeElement(nums []int, val int) int {
	slow, fast := 0, 0
	size := len(nums)
	for fast < size {
		if nums[fast] != val {
			nums[slow] = nums[fast]
			slow++
		}
		fast++
	}
	return slow
}

func removeElement(nums []int, val int) int {
	k := 0
	for _, v := range nums {
		if v != val {
			nums[k] = v
			k++
		}
	}
	return k
}

有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

Python：

#暴力法
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        return sorted([x * x for x in nums])

#双指针
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        n = len(nums)
        res = [0] * n
        i, j = 0, n - 1
        for k in range(n - 1, -1, -1):
            p, q = nums[i] ** 2, nums[j] ** 2
            if p > q:
                res[k] = p
                i += 1
            else:
                res[k] = q
                j -= 1
            k -= 1
        return res

#双指针
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        n = len(nums)
        res = [0] * n
        i, j, k = 0, n - 1, n - 1
        while i <= j:
            p, q = nums[i] ** 2, nums[j] ** 2
            if p > q:
                res[k] = p
                i += 1
            else:
                res[k] = q
                j -= 1
            k -= 1
        return res

Go：

//暴力法
func sortedSquares(nums []int) []int {
	for i := 0; i < len(nums); i++ {
		nums[i] = nums[i] * nums[i]
	}
	sort.Ints(nums)
	return nums
}

//双指针
func sortedSquares(nums []int) []int {
	n := len(nums)
	ans := make([]int, n)
	i, j := 0, n-1
	for pos := n - 1; pos >= 0; pos-- {
		if v, w := nums[i]*nums[i], nums[j]*nums[j]; v > w {
			ans[pos] = v
			i++
		} else {
			ans[pos] = w
			j--
		}
	}
	return ans
}

//双指针
func sortedSquares(nums []int) []int {
	n := len(nums)
	i, j, k := 0, n-1, n-1
	ans := make([]int, n)
	for i <= j {
		lm, rm := nums[i]*nums[i], nums[j]*nums[j]
		if lm > rm {
			ans[k] = lm
			i++
		} else {
			ans[k] = rm
			j--
		}
		k--
	}
	return ans
}

长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

Python：

#滑动窗口
class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        if not nums or sum(nums) < target:
            return 0
        left = right = tmp = 0
        l = len(nums)
        res = l + 1
        while right < l:
            tmp += nums[right]
            while tmp >= target:
                res = min(res, right - left + 1)
                tmp -= nums[left]
                left += 1
            right += 1
        return res

Go：

func minSubArrayLen(target int, nums []int) int {
	l := len(nums)
	left, right, tmp := 0, 0, 0
	res := l + 1
	for right < l {
		tmp += nums[right]
		for tmp >= target {
			if m := right - left + 1; m < res {
				res = m
			}
			tmp -= nums[left]
			left += 1
		}
		right += 1
	}
	if res == l+1 {
		return 0
	}
	return res
}

螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

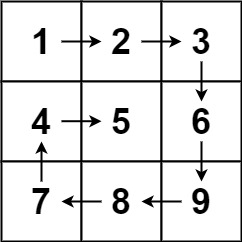
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

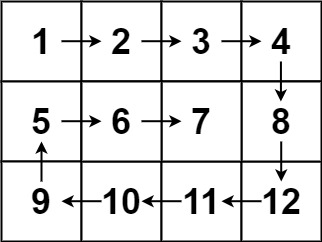
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

模拟矩阵的生成。按照要求，初始位置设为矩阵的左上角，初始方向设为向右。若下一步的位置超出矩阵边界，或者是之前访问过的位置，则顺时针旋转，进入下一个方向。如此反复直至填入 m*n个元素。

Python：

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        m, n = len(matrix), len(matrix[0])
        res = []
        row, col, d = 0, 0, 0
        for i in range(m * n):
            res.append(matrix[row][col])
            matrix[row][col] = True
            dx, dy = dirs[d]
            r, c = row + dx, col + dy
            if r < 0 or r >= m or c < 0 or c >= n or matrix[r][c] == True:
                d = (d + 1) % 4
                dx, dy = dirs[d]
            row, col = row + dx, col + dy
        return res

Go：

func spiralOrder(matrix [][]int) []int {
	dirs := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
	m, n := len(matrix), len(matrix[0])
	res := make([]int, 0, m*n)
	visited := make([][]bool, m)
	for i := 0; i < m; i++ {
		visited[i] = make([]bool, n)
	}
	row, col, dir := 0, 0, 0
	for i := 0; i < m*n; i++ {
		res = append(res, matrix[row][col])
		visited[row][col] = true
		r, c := row+dirs[dir][0], col+dirs[dir][1]
		if r < 0 || r >= m || c < 0 || c >= n || visited[r][c] {
			dir = (dir + 1) % 4
		}
		row, col = row+dirs[dir][0], col+dirs[dir][1]
	}
	return res
}

//由于题目明确说明矩阵元素大小不超过100，可将原矩阵访问过的元素置为101
func spiralOrder(matrix [][]int) []int {
	dirs := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
	m, n := len(matrix), len(matrix[0])
	res := make([]int, 0, m*n)
	row, col, dir := 0, 0, 0
	for i := 0; i < m*n; i++ {
		res = append(res, matrix[row][col])
		matrix[row][col] = 101
		r, c := row+dirs[dir][0], col+dirs[dir][1]
		if r < 0 || r >= m || c < 0 || c >= n || matrix[r][c] == 101 {
			dir = (dir + 1) % 4
		}
		row, col = row+dirs[dir][0], col+dirs[dir][1]
	}
	return res
}

螺旋矩阵II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 20

方法一：模拟矩阵的生成。按照要求，初始位置设为矩阵的左上角，初始方向设为向右。若下一步的位置超出矩阵边界，或者是之前访问过的位置，则顺时针旋转，进入下一个方向。如此反复直至填入 n^2个元素。

方法二：当 num <= tar 时，始终按照从左到右从上到下从右到左从下到上填入顺序循环，每次填入后：
执行 num += 1：得到下一个需要填入的数字；
更新边界：例如从左到右填完后，上边界 t += 1，相当于上边界向内缩 1。

Python：

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        dirs = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        matrix = [[0] * n for _ in range(n)]
        row, col, dirIdx = 0, 0, 0
        for i in range(n * n):
            matrix[row][col] = i + 1
            dx, dy = dirs[dirIdx]
            r, c = row + dx, col + dy
            if r < 0 or r >= n or c < 0 or c >= n or matrix[r][c] > 0:
                dirIdx = (dirIdx + 1) % 4  
                dx, dy = dirs[dirIdx]
            row, col = row + dx, col + dy

        return matrix

class Solution:
    def generateMatrix(self, n: int) -> [[int]]:
        l, r, t, b = 0, n - 1, 0, n - 1
        matrix = [[0] * n for _ in range(n)]
        num, tar = 1, n * n
        while num <= tar:
            for i in range(l, r + 1):
                matrix[t][i] = num
                num += 1
            t += 1
            for i in range(t, b + 1):
                matrix[i][r] = num
                num += 1
            r -= 1
            for i in range(r, l - 1, -1):
                matrix[b][i] = num
                num += 1
            b -= 1
            for i in range(b, t - 1, -1):
                matrix[i][l] = num
                num += 1
            l += 1
        return matrix

Go：

func generateMatrix(n int) [][]int {
	dirs := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
	matrix := make([][]int, n)
	for i := range matrix {
		matrix[i] = make([]int, n)
	}
	row, col, dir := 0, 0, 0
	for i := 0; i < n*n; i++ {
		matrix[row][col] = i + 1
		dx, dy := dirs[dir][0], dirs[dir][1]
		if r, c := row+dx, col+dy; r < 0 || r >= n || c < 0 || c >= n || matrix[r][c] > 0 {
			dir = (dir + 1) % 4
			dx, dy = dirs[dir][0], dirs[dir][1]
		}
		row, col = row+dx, col+dy
	}
	return matrix
}

func generateMatrix(n int) [][]int {
	l, r, t, b := 0, n-1, 0, n-1
	matrix := make([][]int, n)
	for i := 0; i < n; i++ {
		matrix[i] = make([]int, n)
	}
	num, tar := 1, n*n
	for num <= tar {
		for i := l; i <= r; i++ {
			matrix[t][i] = num
			num++
		}
		t++
		for i := t; i <= b; i++ {
			matrix[i][r] = num
			num++
		}
		r--
		for i := r; i >= l; i-- {
			matrix[b][i] = num
			num++
		}
		b--
		for i := b; i >= t; i-- {
			matrix[i][l] = num
			num++
		}
		l++
	}
	return matrix
}