本文属于数据结构专栏文章，适合数据结构入门者学习，涵盖数据结构基础的知识和内容体系，文章在介绍数据结构时会配合上动图演示，方便初学者在学习数据结构时理解和学习，了解数据结构系列专栏点击下方链接。

---

• 博客主页：Duck Bro 博客主页
• 系列专栏：数据结构专栏
• 关注博主，后期持续更新系列文章
• 如果有错误感谢请大家批评指出，及时修改
• 感谢大家点赞👍收藏⭐评论✍

---

数据结构入门 — 二叉树的概念、性质及结构

本文关键字：二叉树、概念、存储结构、性质

---

一、二叉树的概念

二叉树是一种数据结构，由一组节点组成，每个节点最多有两个子节点，称为左子节点和右子节点。二叉树可以为空树，也可以是一个只有根节点而没有子节点的单节点树，或者是一个有多个节点的树，每个节点都有且仅有一个父节点。

对于任意的二叉树都是由以下几种情况复合而成的：

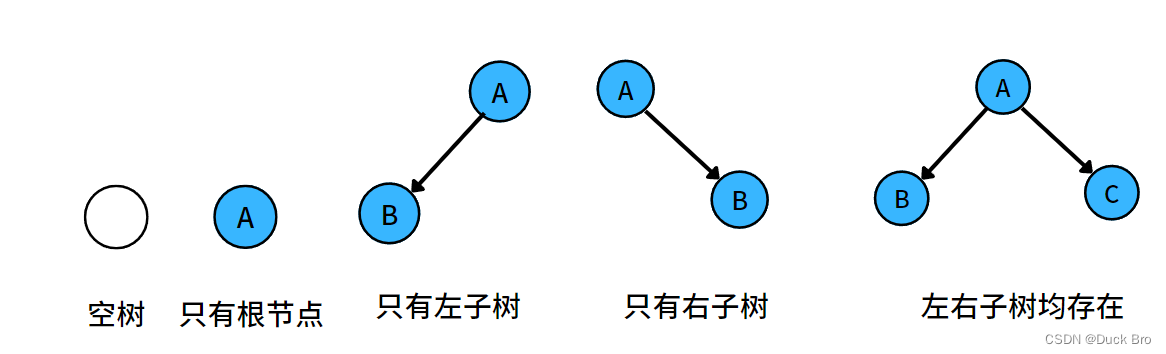
一个二叉树要么为空树，要么由一个根节点和两棵分别称为左子树和右子树的二叉树组成。

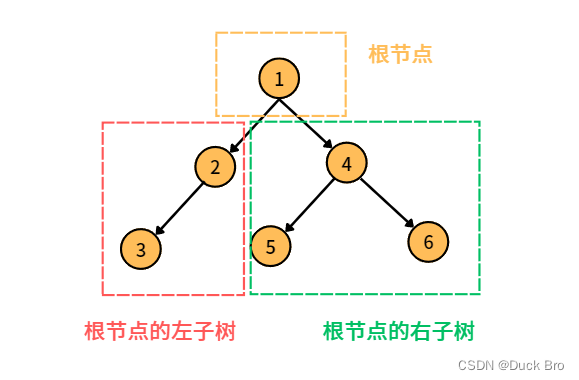
注意：

1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

---

二、特殊的二叉树

特殊的二叉树有很多种，几种特殊的二叉树都有其独特的特点，在不同的场景下有不同的应用

名称	说明
完全二叉树	除了最后一层节点不满以外，其它每层节点数都达到最大值。在最后一层上只缺少右侧连续若干节点。
满二叉树	每个节点都有零或两个子节点，且所有叶子节点都在同一层上。
平衡二叉树	一棵空树或者左右两个子树高度差的绝对值不超过 1，且左右两个子树都是平衡二叉树。
二叉搜索树（BST）	一棵空树或者满足以下特点的二叉树：对于任意节点，左子树中的所有节点小于该节点的值，右子树中的所有节点大于该节点的值。
红黑树	一棵自平衡二叉搜索树，具有以下特点：每个节点要么是红色，要么是黑色，根节点是黑色，叶子节点是黑色的空节点，红色节点的子节点只能是黑色的节点，从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
B 树	一种自平衡的多路搜索树，能够支持对数据的高效操作，主要应用于文件系统和数据库管理系统等领域。

---

三、二叉树的性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有 $2^{(n-1)}$个结点.
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是$2^h-1$ .
3. 对任何一棵二叉树, 如果度为0其叶结点个数为$n_0$ , 度为2的分支结点个数为 ,则有 $n_0=n_2+1$
4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度，$h=lo{g}_2(n+1)$. (ps：$lo{g}_2(n+1)$是log以2
   为底，n+1为对数)
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为 i 的结点有：

1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

---

四、二叉树的结构

二叉树有两种基本的存储结构：顺序存储和链式存储。

1. 顺序存储法

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆后面的文章会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

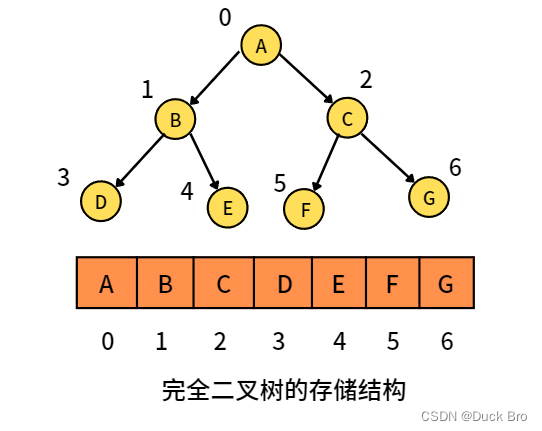
2. 链式存储法

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

---