竞赛链接

https://leetcode.cn/contest/weekly-contest-362/

Q1：2848. 与车相交的点

https://leetcode.cn/problems/points-that-intersect-with-cars/description/

提示：
1 <= nums.length <= 100
nums[i].length == 2
1 <= starti <= endi <= 100

解法1——排序后枚举

排序之后按顺序枚举，每次比较和上个区间结束位置之间的关系。

class Solution {
    public int numberOfPoints(List<List<Integer>> nums) {
        int ans = 0, last = -1;
        Collections.sort(nums, (x, y) -> x.get(0) - y.get(0));
        for (List<Integer> x: nums) {
            ans += Math.max(0, x.get(1) - Math.max(last + 1, x.get(0)) + 1);
            last = Math.max(last, x.get(1));
        }
        return ans;
    }
}

解法2——差分数组⭐

https://leetcode.cn/problems/points-that-intersect-with-cars/solutions/2435384/chai-fen-shu-zu-xian-xing-zuo-fa-by-endl-3xpm/

关于差分可见：【算法基础】1.5 前缀和与差分

class Solution {
    public int numberOfPoints(List<List<Integer>> nums) {
        int[] diff = new int[102];
        // 利用差分将区间内所有位置 +1
        for (List<Integer> p: nums) {
            diff[p.get(0)]++;
            diff[p.get(1) + 1]--;
        }
        int ans = 0, s = 0;
        // 检查各个位置  如果>0则ans++
        for (int d: diff) {
            s += d;
            if (s > 0) ans++;
        }
        return ans;
    }
}

差分数组相关题目列表📕

题目列表来源：分享｜【算法小课堂】差分数组（Python/Java/C++/Go/JS）

1094. 拼车

https://leetcode.cn/problems/car-pooling/

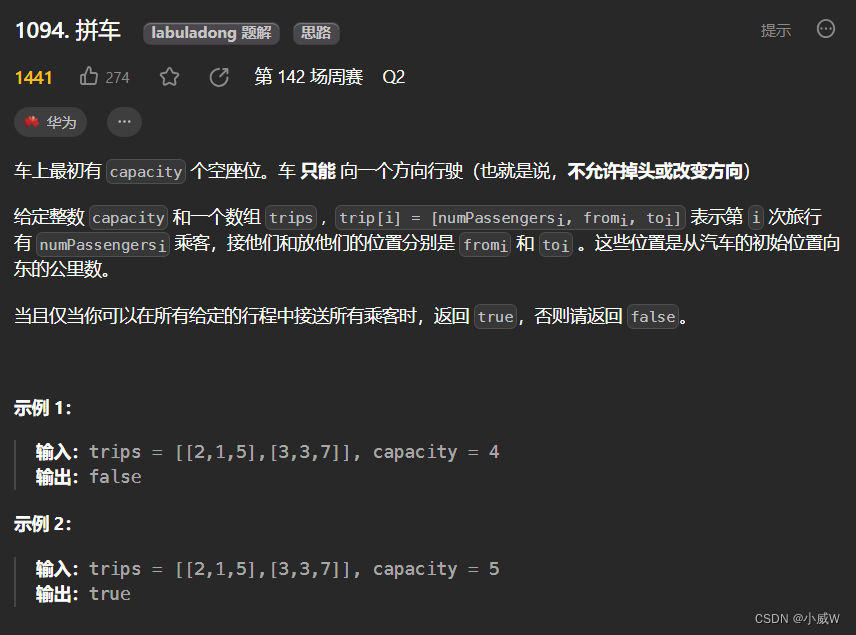
提示：

1 <= trips.length <= 1000
trips[i].length == 3
1 <= numPassengersi <= 100
0 <= fromi < toi <= 1000
1 <= capacity <= 10^5

用差分 表示 from 到 to 的范围内增加了多少人，然后再还原。

class Solution {
    public boolean carPooling(int[][] trips, int capacity) {
        int[] diff = new int[1002];
        // 构造差分数组
        for (int[] t: trips) {
            diff[t[1]] += t[0];
            diff[t[2]] -= t[0];
        }
        // 差分数组的还原
        for (int i = 0; i <= 1000; ++i) {
            if (diff[i] > capacity) return false;
            diff[i + 1] += diff[i];
        }
        return true;
    }
}

1109. 航班预订统计

https://leetcode.cn/problems/corporate-flight-bookings/

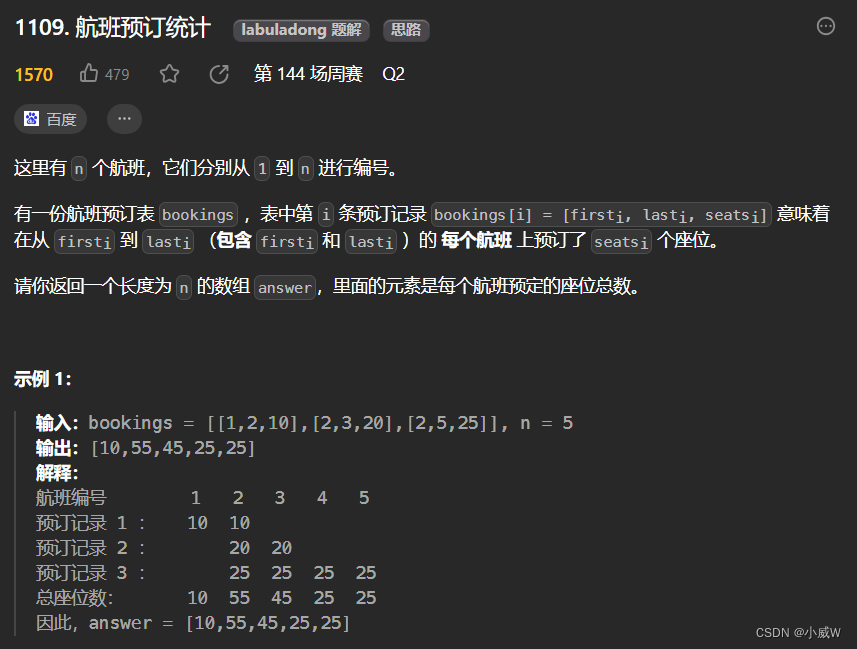
提示
1 <= n <= 2 * 10^4
1 <= bookings.length <= 2 * 10^4
bookings[i].length == 3
1 <= firsti <= lasti <= n
1 <= seatsi <= 10^4

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        int[] ans = new int[n], diff = new int[n + 1];
        for (int[] booking: bookings) {
            diff[booking[0] - 1] += booking[2];
            diff[booking[1]] -= booking[2];
        }
        for (int i = 0; i < n; ++i) {
            ans[i] = diff[i];
            diff[i + 1] += diff[i];
        }
        return ans;
    }
}

2381. 字母移位 II

https://leetcode.cn/problems/shifting-letters-ii/

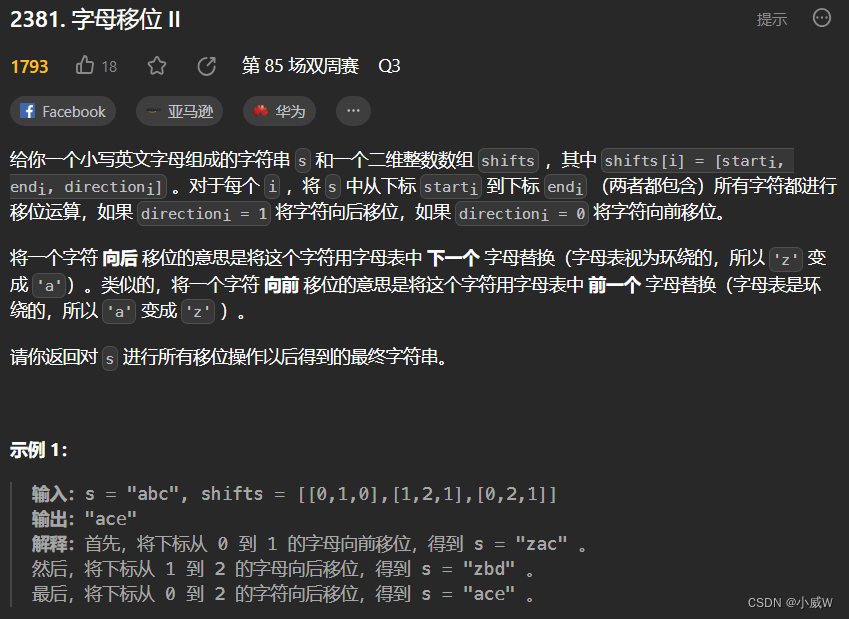
提示
1 <= s.length, shifts.length <= 5 * 10^4
shifts[i].length == 3
0 <= starti <= endi < s.length
0 <= directioni <= 1
s 只包含小写英文字母。

class Solution {
    public String shiftingLetters(String s, int[][] shifts) {
        int n = s.length();
        // 构造差分数组
        int[] diff = new int[n + 1];
        for (int[] shift: shifts) {
            int t = shift[2] == 1? 1: -1;
            diff[shift[0]] += t;
            diff[shift[1] + 1] -= t;
        }
        // 差分数组和答案的还原
        char[] ans = new char[n];
        for (int i = 0; i < n; ++i) {
            ans[i] = op(s.charAt(i), diff[i]);
            diff[i + 1] += diff[i];
        }
        return String.valueOf(ans);
    }

    // 对字符 a 移动 x
    public char op(char a, int x) {
        return (char)(((a - 'a' + x % 26) + 26) % 26 + 'a');
    }
}

2406. 将区间分为最少组数

https://leetcode.cn/problems/divide-intervals-into-minimum-number-of-groups/

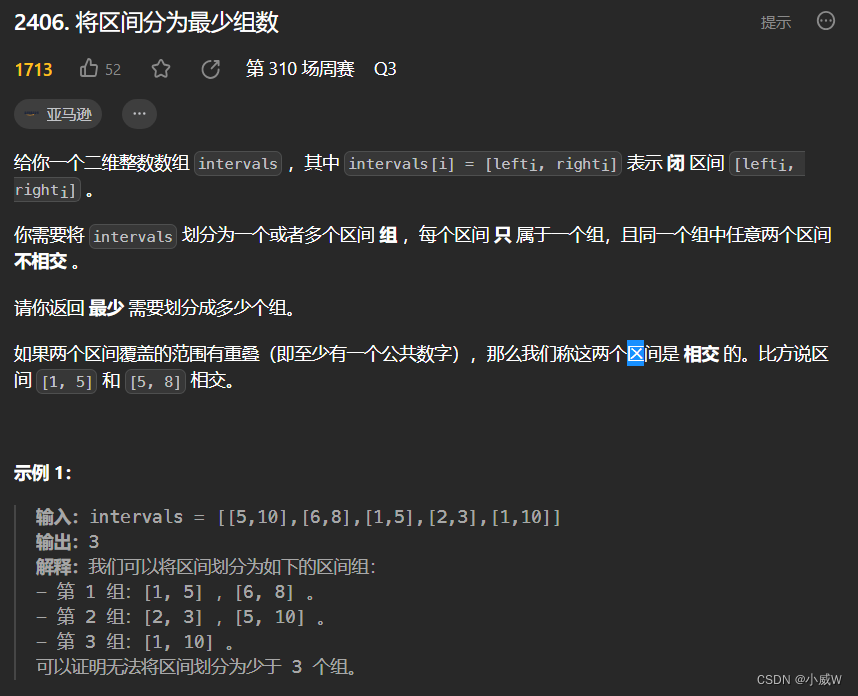
提示：

1 <= intervals.length <= 1^05
intervals[i].length == 2
1 <= lefti <= righti <= 10^6

解法1——排序贪心+优先队列

按照区间的开始位置从小到大排序。
想象每个组合就是一个列表，我们使用有限队列维护这些列表的末尾位置。
这样每次枚举到一个新的区间，检查是否可以放入已有列表中，如果可以，就将一个已有列表的末尾位置换成当前区间的结尾位置。

class Solution {
    public int minGroups(int[][] intervals) {
        Arrays.sort(intervals, (x, y) -> x[0] - y[0]);
        PriorityQueue<Integer> pq = new PriorityQueue<>((x, y) -> x - y);
        for (int[] interval: intervals) {
            if (!pq.isEmpty() && pq.peek() < interval[0]) pq.poll();
            pq.offer(interval[1]);
        }
        return pq.size();
    }
}

解法2——差分数组

差分还原中出现的最大值就是答案。

class Solution {
    public int minGroups(int[][] intervals) {
        TreeMap<Integer, Integer> diff = new TreeMap<>();
        int ans = 0, sum = 0;
        // 计算差分
        for (int[] interval: intervals) {
            diff.merge(interval[0], 1, Integer::sum);
            diff.merge(interval[1] + 1, -1, Integer::sum);
        }
        // 还原差分
        for (Map.Entry<Integer, Integer> entry: diff.entrySet()) {
            sum += entry.getValue();
            ans = Math.max(ans, sum);
        }
        return ans;
    }
}

2772. 使数组中的所有元素都等于零

https://leetcode.cn/problems/apply-operations-to-make-all-array-elements-equal-to-zero/

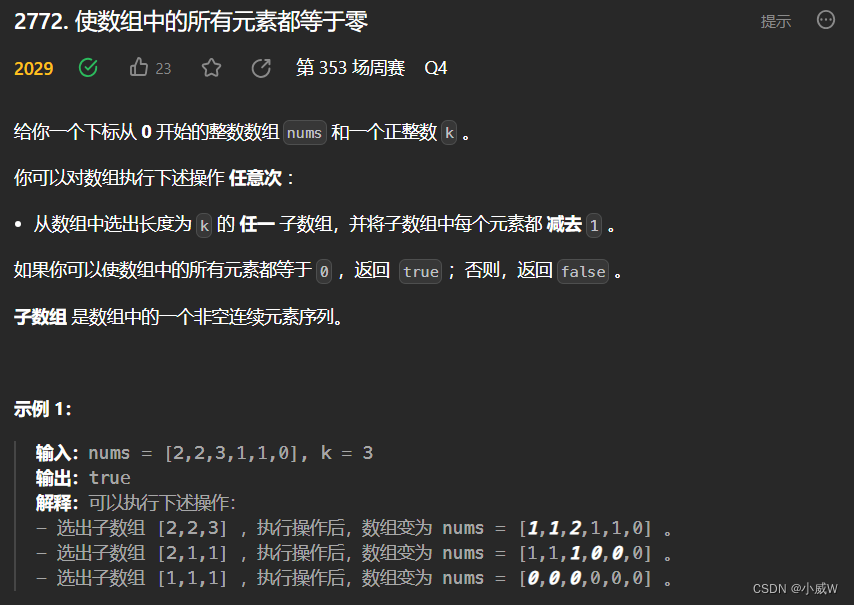
提示：

1 <= k <= nums.length <= 10^5
0 <= nums[i] <= 10^6

有点差分的思想，又不太一样。

贪心地从前往后枚举每一个位置，只要 > 0 就减，< 0 就返回 false。

class Solution {
    public boolean checkArray(int[] nums, int k) {
        int n = nums.length, diff = 0, ans = 0;
        int[] x = new int[n];
        for (int i = 0; i < n; ++i) {
            if (i >= k) diff -= x[i - k];
            if (nums[i] > diff) {
                if (n - i < k) return false;
                ans += nums[i] - diff;      // 更新答案
                x[i] = nums[i] - diff;      // 记录这个位置减去了多少
                diff = nums[i];             // 更新diff
            } else if (nums[i] < diff) return false;
        }
        return true;
    }
}

2528. 最大化城市的最小供电站数目（⭐差分数组 + 二分查找答案）

https://leetcode.cn/problems/maximize-the-minimum-powered-city/

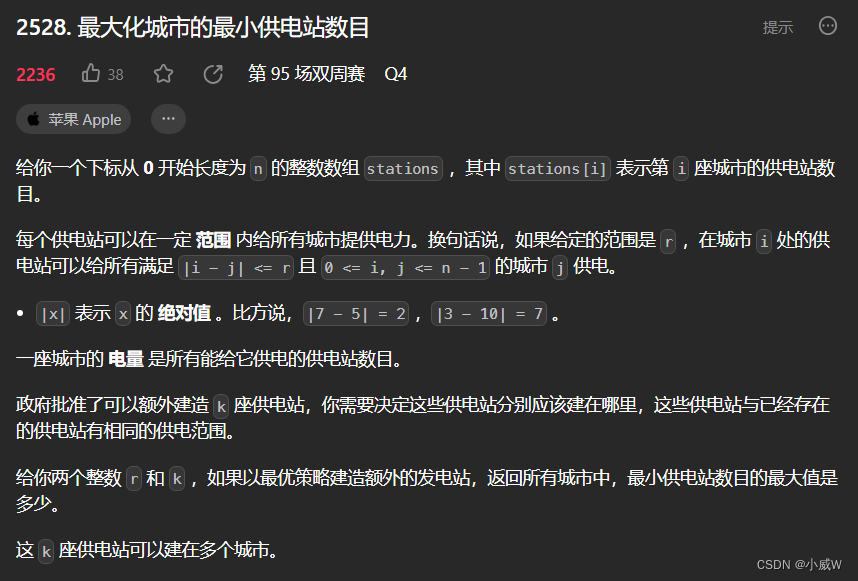
提示：
n == stations.length
1 <= n <= 10^5
0 <= stations[i] <= 10^5
0 <= r <= n - 1
0 <= k <= 10^9

看到「最大化最小值」或者「最小化最大值」就要想到二分答案，这是一个固定的套路。

class Solution {
    public long maxPower(int[] stations, int r, int k) {
        int n = stations.length;
        long mn = Long.MAX_VALUE;
        // 计算差分数组
        long[] cnt = new long[n + 1];
        for (int i = 0; i < n; ++i) {
            cnt[Math.max(0, i - r)] += stations[i];
            cnt[Math.min(n, i + r + 1)] -= stations[i];
        }
        // 差分数组的还原
        for (int i = 0; i < n; ++i) {
            cnt[i + 1] += cnt[i];
            mn = Math.min(mn, cnt[i]);
        }
        // 二分查找答案
        long left = mn, right = mn + k;
        while (left < right) {
            long mid = left + right + 1 >> 1;
            if (!check(cnt, mid, r, k)) right = mid - 1;
            else left = mid;
        }
        return left;
    }

    // check过程类似 T2772. 使数组中的所有元素都等于零
    public boolean check(long[] cnt, long x, int r, int k) {
        long diff = 0;
        int n = cnt.length - 1;
        long[] d = new long[n];
        for (int i = 0; i < n; ++i) {
            if (i >= 2 * r + 1) diff -= d[i - 2 * r - 1];
            if (cnt[i] + diff < x) {
                d[i] = x - cnt[i] - diff;
                k -= d[i];
                diff = x - cnt[i];
            }
        }
        return k >= 0;
    }
}

最大化最小化相关题目列表📕

题目列表来源：https://leetcode.cn/problems/maximize-the-minimum-powered-city/solutions/2050272/er-fen-da-an-qian-zhui-he-chai-fen-shu-z-jnyv/

2439. 最小化数组中的最大值

https://leetcode.cn/problems/minimize-maximum-of-array/

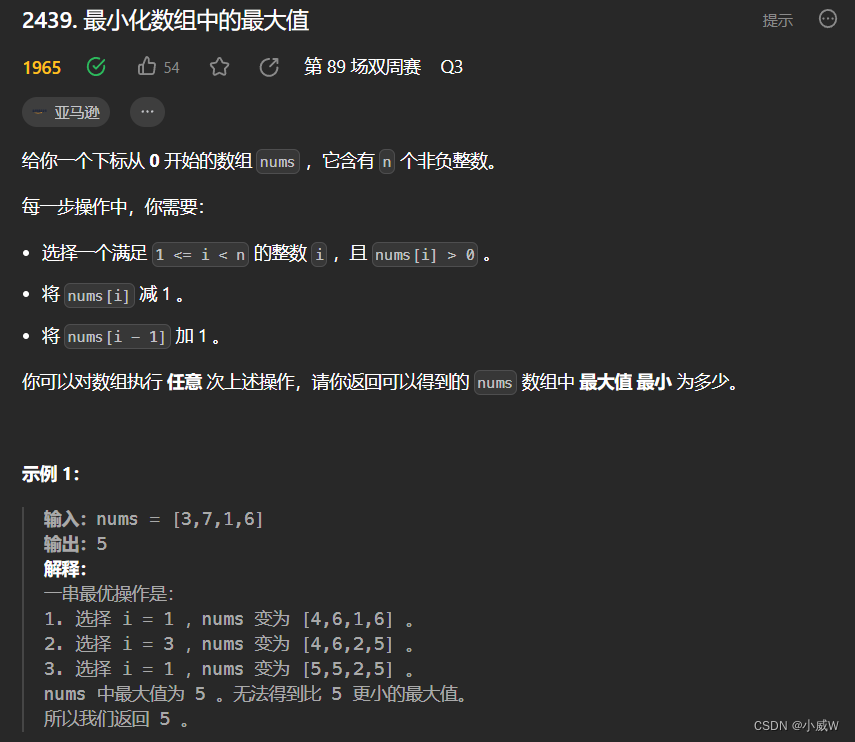
提示：
n == nums.length
2 <= n <= 10^5
0 <= nums[i] <= 10^9

解法1——二分答案

class Solution {
    public int minimizeArrayValue(int[] nums) {
        int l = Integer.MAX_VALUE, r = Integer.MIN_VALUE;
        for (int x: nums) {
            l = Math.min(l, x);
            r = Math.max(r, x);
        }
        while (l < r) {
            int mid = l + r >> 1;
            if (check(mid, nums)) r = mid;
            else l = mid + 1;
        }
        return l;
    }

    public boolean check(int k, int[] nums) {
        if (nums[0] > k) return false;
        long d = k - nums[0];           // 使用long防止溢出
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] <= k) d += k - nums[i];
            else {
                d -= nums[i] - k;
                if (d < 0) return false;
            }
        }
        return true;
    }
}

解法2——分类讨论O(n)

首先最大值的最小值是 nums[0]。
对于 nums[1]，当其 < nums[0] 时，答案还是 nums[0]；当其 > nums[0] 时，则答案是两者的平均向上取整。

class Solution {
    public int minimizeArrayValue(int[] nums) {
        long mx = 0, sum = 0;
        for (int i = 0; i < nums.length; ++i) {
            sum += nums[i];
            // (sum + i) / (i + 1) 是因为要向上取整
            mx = Math.max(mx, (sum + i) / (i + 1));     
        }
        return (int)mx;
    }
}

2513. 最小化两个数组中的最大值（二分答案+lcm+容斥原理）🐂好题！

https://leetcode.cn/problems/minimize-the-maximum-of-two-arrays/

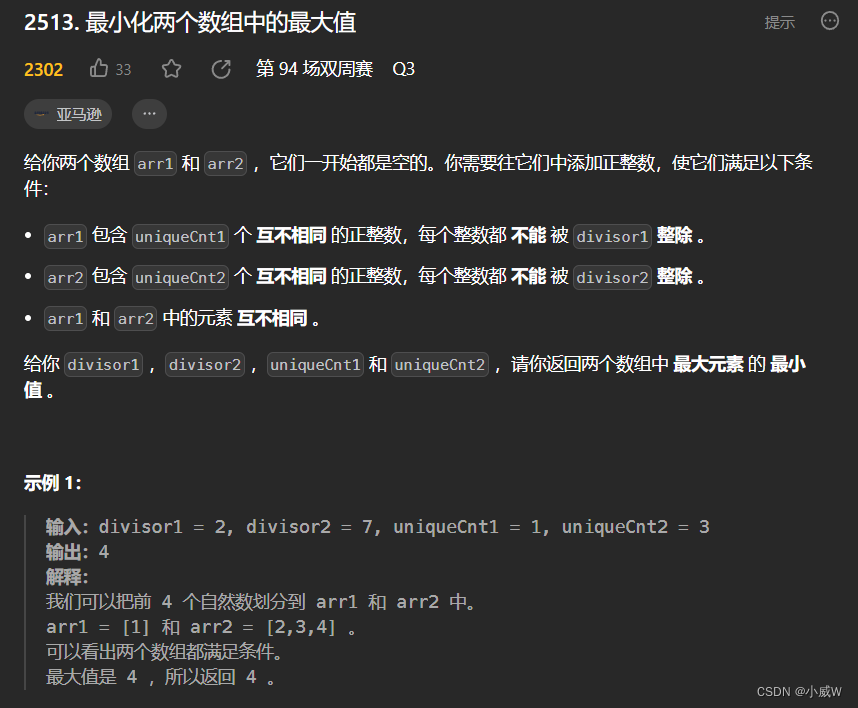
提示：
2 <= divisor1, divisor2 <= 10^5
1 <= uniqueCnt1, uniqueCnt2 < 10^9
2 <= uniqueCnt1 + uniqueCnt2 <= 10^9

二分答案。

class Solution {
    public int minimizeSet(int divisor1, int divisor2, int uniqueCnt1, int uniqueCnt2) {
        long l = 0, r = (long)Integer.MAX_VALUE;
        while (l < r) {
            long mid = l + r >> 1;
            // 两个数组不能选择的数字数量
            long x = mid / divisor1, y = mid / divisor2, z = mid / lcm(divisor1, divisor2);
            long sum = uniqueCnt1 + uniqueCnt2 + z;         // 至少需要的数字数量
            // arr1不能使用的，看arr2能不能使用；反之同理
            sum += Math.max(0, x - z - uniqueCnt2) + Math.max(0, y - z - uniqueCnt1);
            if (sum <= mid) r = mid;
            else l = mid + 1;
        }
        return (int)l;
    }

    // 最小公倍数
    public long lcm(long x, long y) {
        return x / gcd(x, y) * y;
    }

    // 最大公因数
    public long gcd(long x, long y) {
        return y == 0? x: gcd(y, x % y);
    }
}

2517. 礼盒的最大甜蜜度（二分答案）

https://leetcode.cn/problems/maximum-tastiness-of-candy-basket/

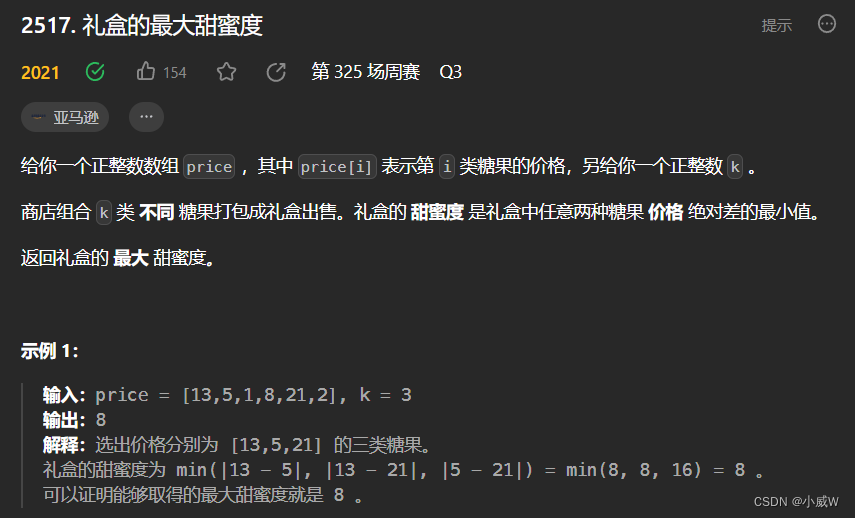
提示：
2 <= k <= price.length <= 10^5
1 <= price[i] <= 10^9

class Solution {
    public int maximumTastiness(int[] price, int k) {
        Arrays.sort(price);
        int n = price.length, l = 0, r = price[n - 1] - price[0];
        while (l < r) {
            int mid = l + r + 1 >> 1;
            int s = 1, last = price[0];
            for (int i = 1; i < n && s < k; ++i) {
                if (price[i] - last >= mid) {
                    s++;
                    last = price[i];
                }
            }
            if (s < k) r = mid - 1;
            else l = mid;
        }
        return l;
    }
}

Q2：2849. 判断能否在给定时间到达单元格（脑筋急转弯、贪心）

https://leetcode.cn/problems/determine-if-a-cell-is-reachable-at-a-given-time/

提示：
1 <= sx, sy, fx, fy <= 109
0 <= t <= 10^9

斜着走，一步顶两步——相当于可以同时横着走和竖着走。 那么只要满足垂直和水平方向中最长的那个距离就好了。

注意有个特例是：只走一步时，如果起点和终点相同就不可以了。

class Solution {
    public boolean isReachableAtTime(int sx, int sy, int fx, int fy, int t) {
        if (sx == fx && sy == fy && t == 1) return false;		// 特例
        return t >= Math.max(Math.abs(sx - fx), Math.abs(sy - fy));
    }
}

Q3：2850. 将石头分散到网格图的最少移动次数⭐⭐⭐（全排列和状态压缩）

https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/

提示：

grid.length == grid[i].length == 3
0 <= grid[i][j] <= 9
grid 中元素之和为 9

解法1——枚举全排列

https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/

将起始点和终点分别放入两个列表，做全排列匹配。
枚举所有全排列，比较各种情况下的移动次数，得出最小移动次数。

class Solution {
    int ans = Integer.MAX_VALUE, sum = 0;
    boolean[] st = new boolean[9];

    public int minimumMoves(int[][] grid) {
        // 将起始点和终点放入列表
        List<int[]> src = new ArrayList<>(), dst = new ArrayList<>();
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                while (grid[i][j] > 1) {
                    src.add(new int[]{i, j});
                    grid[i][j]--;
                }
                if (grid[i][j] == 0) dst.add(new int[]{i, j});
            }
        }
        // dfs全排列
        dfs(0, src, dst);
        return ans;
    }

    public void dfs(int i, List<int[]> src, List<int[]> dst) {
        if (i == src.size()) {
            ans = Math.min(ans, sum);
            return;
        }
        for (int j = 0; j < dst.size(); ++j) {
            if (!st[j]) {
                int[] s = src.get(i), d = dst.get(j);
                sum += Math.abs(s[0] - d[0]) + Math.abs(s[1] - d[1]);
                st[j] = true;
                dfs(i + 1, src, dst);
                sum -= Math.abs(s[0] - d[0]) + Math.abs(s[1] - d[1]);
                st[j] = false;
            }
        }
    }
}

解法2——最小费用最大流 （TODO）

https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/

在这里插入代码片

解法3——状压DP

https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435319/zhuang-ya-dp-by-tsreaper-jiw0/

状态压缩DP相比全排列速度更快（48ms vs 3ms）

class Solution {
    public int minimumMoves(int[][] grid) {
        // 起始点和目的点放入两个列表
        List<int[]> L = new ArrayList<>(), R = new ArrayList<>();
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (grid[i][j] == 0) R.add(new int[]{i, j});
                else {
                    for (; grid[i][j] > 1; grid[i][j]--) {
                        L.add(new int[]{i, j});
                    }
                }
            }
        }

        // 状态压缩DP
        int n = L.size();
        int[] dp = new int[1 << n];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 1; i < (1<<n); ++i) {
            // 计算 i 中有几个二进制等于 1——为了确定当前目的点是哪个
            int cnt = 0;
            for (int j = 0; j < n; ++j) {
                cnt += i >> j & 1;
            }
            // 状态转移
            for (int j = 0; j < n; ++j) {   // 枚举所有目标点
                if ((i >> j & 1) == 1) {    // 检查是否为1，即是否可以从前面转移过来
                    dp[i] = Math.min(dp[i], dp[i ^ (1 << j)] + cost(R.get(cnt - 1), L.get(j)));
                }
            }
        }
        return dp[(1<<n) - 1];
    }

    public int cost(int[] a, int[] b) {
        return Math.abs(a[0] - b[0]) + Math.abs(a[1] - b[1]);
    }
}

涉及到「匹配」的题目列表📕

题单来源：https://leetcode.cn/problems/minimum-moves-to-spread-stones-over-grid/solutions/2435313/tong-yong-zuo-fa-zui-xiao-fei-yong-zui-d-iuw8/

1947. 最大兼容性评分和

https://leetcode.cn/problems/maximum-compatibility-score-sum/

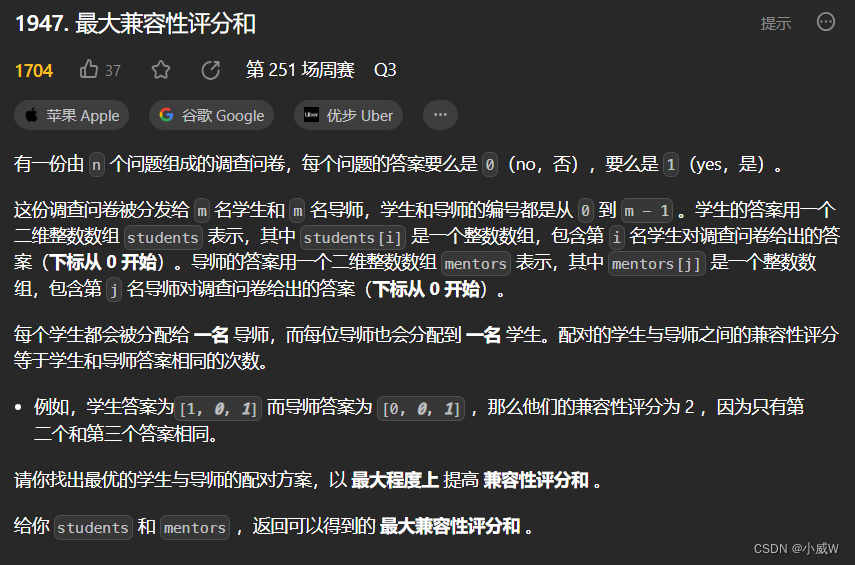
提示：
m == students.length == mentors.length
n == students[i].length == mentors[j].length
1 <= m, n <= 8
students[i][k] 为 0 或 1
mentors[j][k] 为 0 或 1

解法1——枚举全排列

数据范围很小，可以枚举出所有学生和老师之间匹配的方案。

class Solution {
    int ans = 0;
    boolean[] st = new boolean[8];

    public int maxCompatibilitySum(int[][] students, int[][] mentors) {
        // 全排列
        dfs(students, mentors, 0, 0);
        return ans;
    }

    public void dfs(int[][] students, int[][] mentors, int i, int sum) {
        if (i == students.length) {
            ans = Math.max(ans, sum);
            return;
        }
        for (int j = 0; j < mentors.length; ++j) {
            if (st[j]) continue;
            st[j] = true;
            dfs(students, mentors, i + 1, sum + cp(students[i], mentors[j]));
            st[j] = false;
        }
    }

    // 计算某个学生和某个老师的兼容性评分
    public int cp(int[] s, int[] t) {
        int res = 0;
        for (int i = 0; i < s.length; ++i) {
            if (s[i] == t[i]) res++;
        }
        return res;
    }
}

解法2——状态压缩DP

class Solution {
    public int maxCompatibilitySum(int[][] students, int[][] mentors) {
        int n = students.length;
        int[][] dp = new int[n + 1][1<<n];  // dp[i][j]表示匹配完i个老师，和集合j的学生的最大匹配和
        // 枚举每个状态
        for (int i = 1; i < (1<<n); ++i) {
            int idx = Integer.bitCount(i);  // 计算该匹配哪个老师了
            // 枚举每个学生
            for (int j = 0; j < n; ++j) {
                if ((i >> j & 1) == 1) {    // 如果可以转移
                    dp[idx][i] = Math.max(dp[idx][i], dp[idx - 1][i ^ (1<<j)] + cp(students[j], mentors[idx - 1]));
                }
            }
        }
        return dp[n][(1<<n) - 1];
    }

    // 计算某个学生和某个老师的兼容性评分
    public int cp(int[] s, int[] t) {
        int res = 0;
        for (int i = 0; i < s.length; ++i) {
            if (s[i] == t[i]) res++;
        }
        return res;
    }
}

1349. 参加考试的最大学生数🚹（状态压缩DP）

https://leetcode.cn/problems/maximum-students-taking-exam/

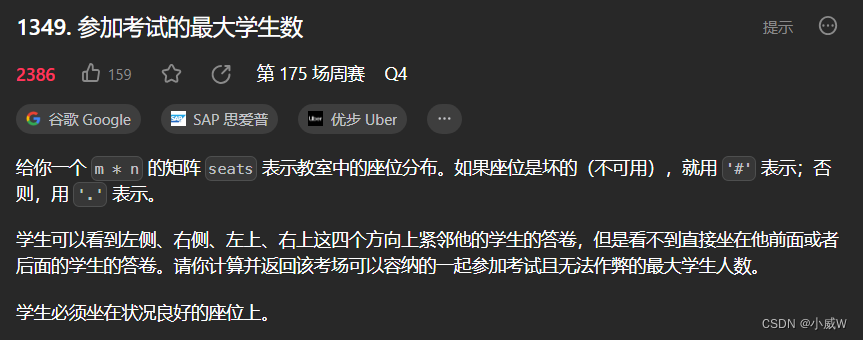
提示：
seats 只包含字符 '.' 和'#'
m == seats.length
n == seats[i].length
1 <= m <= 8
1 <= n <= 8

将每一行选择的位置用一个int变量表示。

枚举每一行，再枚举该行的状态，然后枚举上一行的状态，检测是否合理且可以转移过来。
最后的答案就是最后一行各个状态的最大值。

---

这里的合理包括：

1. 该行本身要合理，—— 都要坐在正常的椅子上；同一行的两个学生不能挨边坐。
2. 每一行和上一行之间不能有冲突——如果上一行的某一列已经坐人了，那么该行该列的左右两侧就不能坐人了。

class Solution {
    public int maxStudents(char[][] seats) {
        int m = seats.length, n = seats[0].length;
        int[] states = new int[m];
        for (int i = 0; i < m; ++i) {
            states[i] = getMask(seats[i]);
        }
        // 一共m行，每行1<<n种状态
        int[][] dp = new int[m + 1][1 << n];
        for (int i = 0; i < 1<<n; ++i) {
            // 判断 i 是不是 states[0] 的子集 && 自己不冲突
            if (check(states[0], i) && op(i)) {
                dp[0][i] = Integer.bitCount(i);
            }
        }
        // 枚举每一行
        for (int i = 1; i < m; ++i) {
            // 枚举这一行的每个状态
            for (int j = 0; j < 1<<n; ++j) {
                if (!check(states[i], j)) continue;     // 如果这个状态不合理，就跳过
                // 枚举上一行的每个状态
                for (int k = 0; k < 1<<n; ++k) {
                    if (!check(states[i - 1], k)) continue; // 如果这个状态不合理，就跳过
                    if (!confilt(k, j)) {               // 如果这个状态和上一行不冲突
                        dp[i][j] = Math.max(dp[i][j], dp[i - 1][k] + Integer.bitCount(j));
                    }
                }
                
            }
            System.out.println();
        }
        return Arrays.stream(dp[m - 1]).max().getAsInt();
    }

    // 将一行的状态用一个int表示
    public int getMask(char[] state) {
        int res = 0;
        for (int i = 0; i < state.length; ++i) {
            if (state[i] == '.') res |= 1 << i;
        }
        return res;
    }

    // 检查状态x是否是状态state的子集，即是否可选 && 这个状态x本身合法
    public boolean check(int state, int x) {
        if ((state | x) != state) return false;      // 需要x是state的子集
        return op(x);       
    }

    // 检查x是否和y作为上一行冲突
    public boolean confilt(int x, int y) {
        for (int i = 0; i < 10; ++i) {
            if ((x >> i & 1) == 1) {    // 如果x这个位置有了
                // 那么y的相差一列的位置就不能有了
                if ((y >> i + 1 & 1) == 1 || (y >> i - 1 & 1) == 1) {
                    return true;
                }
            }
        }
        return false;
    }

    // 检查这一行的状态本身是否合理，即检查是否有两个学生坐在挨边的位置上
    public boolean op(int x) {
        for (int i = 0; i < 9; ++i) {
            if ((x >> i & 1) == 1 && (x >> i + 1 & 1) == 1) return false;
        }
        return true;
    }
}

LCP 04. 覆盖🚹（TODO 二分图匹配 & 状态压缩DP）

https://leetcode.cn/problems/broken-board-dominoes/

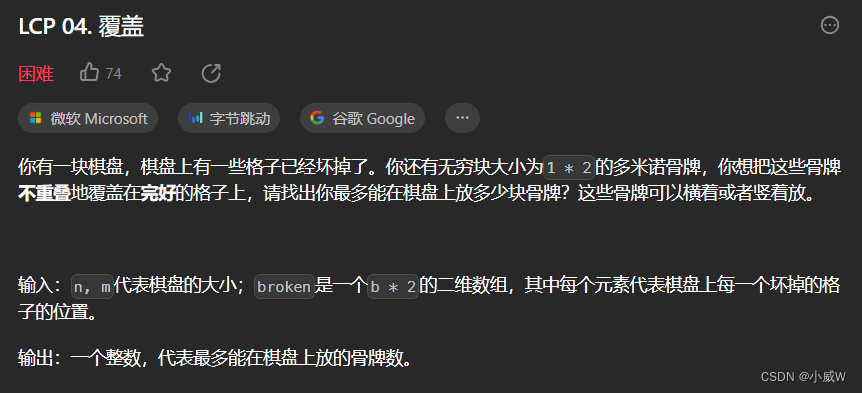
限制：
1 <= n <= 8
1 <= m <= 8
0 <= b <= n * m

解法1——二分图匹配

在这里插入代码片

解法2——状态压缩DP

在这里插入代码片

1879. 两个数组最小的异或值之和（状态压缩DP）

https://leetcode.cn/problems/minimum-xor-sum-of-two-arrays/

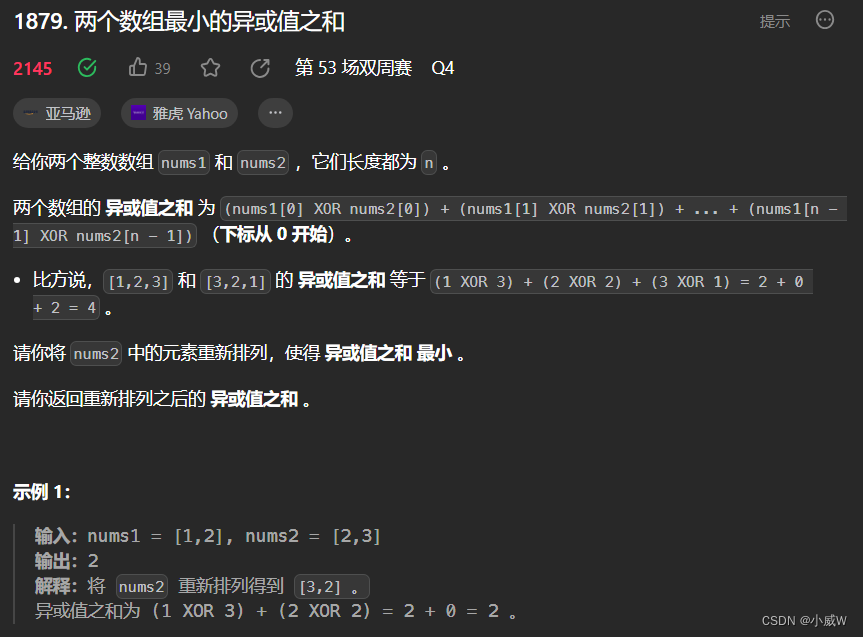
提示：
n == nums1.length
n == nums2.length
1 <= n <= 14
0 <= nums1[i], nums2[i] <= 10^7

class Solution {
    public int minimumXORSum(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int[][] dp = new int[n + 1][1 << n];
        for (int i = 0; i <= n; ++i) Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
        dp[0][0] = 0;
        // 枚举nums1的每个状态
        for (int i = 1; i < 1<<n; ++i) {
            int cnt = Integer.bitCount(i);
            // 枚举每个位置
            for (int j = 0; j < n; ++j) {
                if ((i >> j & 1) == 1) {
                    dp[cnt][i] = Math.min(dp[cnt][i], dp[cnt - 1][i ^ (1<<j)] + (nums1[j] ^ nums2[cnt - 1]));
                }
            }
        }
        return dp[n][(1<<n) - 1];
    }
}

2172. 数组的最大与和（状态压缩DP）

https://leetcode.cn/problems/maximum-and-sum-of-array/

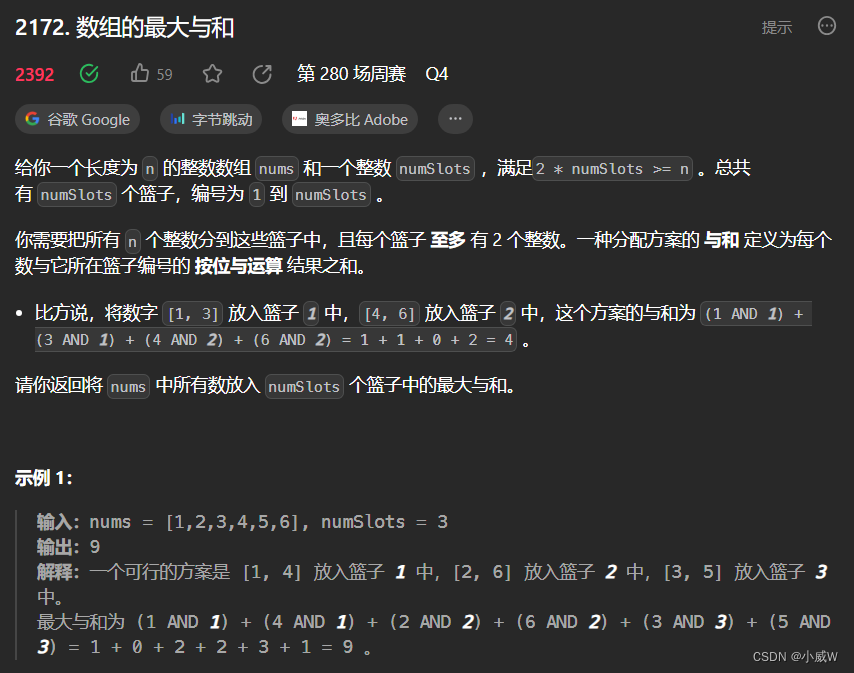
提示：
n == nums.length
1 <= numSlots <= 9
1 <= n <= 2 * numSlots
1 <= nums[i] <= 15

每个篮子可以放最多 2 个数字，那么可以分成有 2 组一模一样的篮子处理。

注意——要将篮子的使用集合作为状态。

class Solution {
    public int maximumANDSum(int[] nums, int numSlots) {
        int n = nums.length, m = 2 * numSlots, ans = 0;
        int[] dp = new int[1<<m];   // m个篮子的状态
        // 枚举每个篮子被选择情况
        for (int i = 1; i < 1<<m; ++i) {
            // 计算该放入那个num了
            int cnt = Integer.bitCount(i);
            if (cnt > n) continue;
            // 枚举每个被选择的篮子
            for (int j = 0; j < m; ++j) {
                if ((i >> j & 1) == 1) {
                    dp[i] = Math.max(dp[i], dp[i ^ (1<<j)] + (nums[cnt - 1] & (j % numSlots + 1)));
                }
            }
            ans = Math.max(ans, dp[i]);
        }
        return ans;
    }
}

Q4：2851. 字符串转换⭐

https://leetcode.cn/problems/string-transformation/

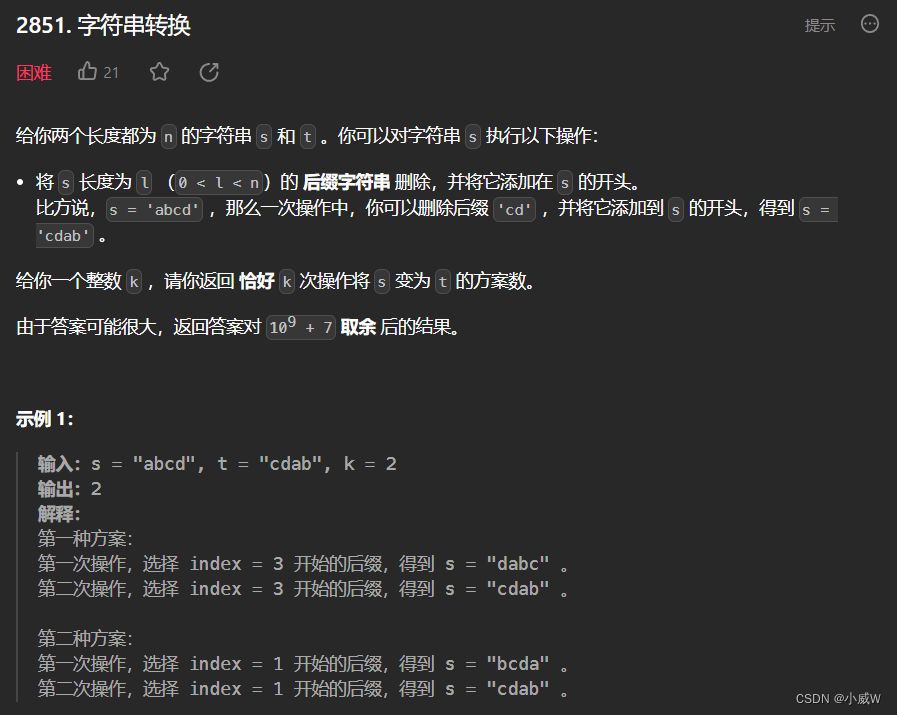
提示：
2 <= s.length <= 5 * 10^5
1 <= k <= 10^15
s.length == t.length
s 和 t 都只包含小写英文字母。

解法1——KMP + 矩阵快速幂优化 DP 🐂

https://leetcode.cn/problems/string-transformation/solutions/2435348/kmp-ju-zhen-kuai-su-mi-you-hua-dp-by-end-vypf/

计算有多少个 s 的循环同构字符串等于 t，记作 c。这可以用 KMP 等字符串匹配算法解决，即寻找 t 在 s+s（去掉最后一个字符）中的出现次数。（用KMP计算出 s + s 中有几个 t）
关于 KMP 可见：我一定要 学会KMP字符串匹配

下面使用动态规划来解决该问题——
定义 f[i][0] 表示 i 次操作后等于 t 的方案数，f[i][1] 表示 i 次操作后不等于 t 的方案数。

发现 DP 递推式可以写成矩阵乘法形式，因此可以使用矩阵快速幂来优化。（所谓矩阵快速幂，和普通快速幂的思想是一样的。）

快速幂可以完成从 $O(n)$ 到 $O(\log n)$ 的优化。

Q：为什么必须要使用矩阵快速幂？
A：因为 k 的数据范围很大。（$\log n$ 对应的数据范围是 $10^{18}$）

class Solution {
    final long MOD = (long)1e9 + 7;

    public int numberOfWays(String s, String t, long k) {
        int n = s.length();
        // kmp 求出 s+s(去掉最后一个字符) 中有几个 t
        int c = kmpSearch(s + s.substring(0, n - 1), t);
        // 递推矩阵
        long[][] m = {
            {c - 1, c},
            {n - c, n - 1 - c},
        };
        m = pow(m, k);      // 矩阵快速幂求结果
        // 根据 s==t？ 判断初始状态 对应的答案
        return s.equals(t)? (int) m[0][0]: (int) m[0][1];
    }

    // kmp 返回 s 中有多少个 t
    public int kmpSearch(String s, String t) {
        int[] next = getNext(s.toCharArray());
        int c = 0;
        for (int i = 0, j = -1; i < s.length(); ++i) {
            while (j != -1 && s.charAt(i) != t.charAt(j + 1)) j = next[j];
            if (s.charAt(i) == t.charAt(j + 1)) j++;
            if (j == t.length() - 1) {
                c++;
                j = next[j];    // 匹配成功之后，记得要更新 j = next[j]
            }
        }
        return c;
    }

    // 求 next 数组
    public int[] getNext(char[] s) {
        int n = s.length;
        int[] next = new int[n];
        next[0] = -1;
        for (int i = 1, j = -1; i < n; ++i) {
            while (j != -1 && s[i] != s[j + 1]) j = next[j];
            if (s[i] == s[j + 1]) j++;
            next[i] = j;
        }
        return next;
    }

    // 矩阵快速幂
    public long[][] pow(long[][] a, long n) {
        long[][] res = {{1, 0}, {0, 1}};
        for (; n > 0; n /= 2) {
            if (n % 2 == 1) {
                res = multiply(res, a);
            }
            a = multiply(a, a);
        }
        return res;
    }

    // 矩阵乘法
    public long[][] multiply(long[][] a, long[][] b) {
        long[][] c = new long[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
            }
        }
        return c;
    }
}

解法2——找规律，无需矩阵快速幂（TODO）

https://leetcode.cn/problems/string-transformation/solutions/2435714/cjavapython-bu-xu-yao-ju-zhen-kuai-su-mi-cukc/

在这里插入代码片

[矩阵快速幂] 题目列表📕

题目列表来源：https://leetcode.cn/problems/string-transformation/solutions/2435348/kmp-ju-zhen-kuai-su-mi-you-hua-dp-by-end-vypf/

70. 爬楼梯

https://leetcode.cn/problems/climbing-stairs/

提示：
1 <= n <= 45

解法1——线性DP

class Solution {
    public int climbStairs(int n) {
        if (n <= 1) return n;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n - 1];
    }
}

解法2——矩阵快速幂

根据递推公式，可以得出矩阵快速幂的矩阵是什么。

class Solution {
    public int climbStairs(int n) {
        if (n <= 2) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n - 2)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1,dp[1] = 2
        int[][] res = {
            {2, 0},
            {1, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

也可以更简洁一些，从 dp[0] 开始写，代码如下：

class Solution {
    public int climbStairs(int n) {
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1
        int[][] res = {
            {1, 0},
            {0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

509. 斐波那契数

https://leetcode.cn/problems/fibonacci-number/

提示：
0 <= n <= 30

跟上一题差不多，注意初始值变了。

class Solution {
    public int fib(int n) {
        if (n == 0) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1},
            {1, 0}
        };
        return pow(m, n - 1)[0][0];
    }

    public int[][] pow(int[][] m, int k) {
        // dp[0] = 1
        int[][] res = {
            {1, 0},
            {0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[2][2];
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 2; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j];
            }
        }
        return res;
    }
}

1137. 第 N 个泰波那契数

https://leetcode.cn/problems/n-th-tribonacci-number/

提示：
0 <= n <= 37
答案保证是一个 32 位整数，即 answer <= 2^31 - 1。

对矩阵稍作修改即可。

class Solution {
    public int tribonacci(int n) {
        if (n <= 1) return n;
        // m是根据递推公式来的
        int[][] m = {
            {1, 1, 1},
            {1, 0, 0},
            {0, 1, 0}
        };
        return pow(m, n - 2)[0][0];
    }

        public int[][] pow(int[][] m, int k) {
        // dp[0] = 0, dp[1] = 1, dp[2] = 1
        int[][] res = {
            {1, 0, 0},
            {1, 0, 0},
            {0, 0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public int[][] mul(int[][] x, int[][] y) {
        int[][] res = new int[3][3];
        for (int i = 0; i < 3; ++i) {
            for (int j = 0; j < 3; ++j) {
                res[i][j] = x[i][0] * y[0][j] + x[i][1] * y[1][j] + x[i][2] * y[2][j];
            }
        }
        return res;
    }
}

1220. 统计元音字母序列的数目

https://leetcode.cn/problems/count-vowels-permutation/

提示：
1 <= n <= 2 * 10^4

解法1——线性DP

class Solution {
    final long MOD = (int)1e9 + 7;
    public int countVowelPermutation(int n) {
        long[][] dp = new long[n][5];
        Arrays.fill(dp[0], 1);
        for (int i = 1; i < n; ++i) {
            dp[i][0] = dp[i - 1][1];
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][3] + dp[i - 1][4]) % MOD;
            dp[i][3] = (dp[i - 1][2] + dp[i - 1][4]) % MOD;
            dp[i][4] = dp[i - 1][0];
        }
        long ans = 0;
        for (long x: dp[n - 1]) ans = (ans + x) % MOD;
        return (int)ans;
    }
}

解法2——矩阵快速幂优化DP

class Solution {
    final long MOD = (int)1e9 + 7;

    public int countVowelPermutation(int n) {
        long[][] m = {
            {0, 1, 0, 0, 0},
            {1, 0, 1, 0, 0},
            {1, 1, 0, 1, 1},
            {0, 0, 1, 0, 1},
            {1, 0, 0, 0, 0}
        };
        long[][] res = pow(m, n - 1);
        long ans = 0;
        for (int i = 0; i < 5; ++i) ans = (ans + res[i][0]) % MOD;
        return (int)ans;
    }

    public long[][] pow(long[][] m, int k) {
        long[][] res = {
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0},
            {1, 0, 0, 0, 0}
        };
        for (; k != 0; k /= 2) {
            if (k % 2 == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public long[][] mul(long[][] x, long[][] y) {
        long[][] res = new long[5][5];
        for (int i = 0; i < 5; ++i) {
            for (int j = 0; j < 5; ++j) {
                res[i][j] = (x[i][0] * y[0][j] + x[i][1] * y[1][j] + x[i][2] * y[2][j] + x[i][3] * y[3][j] + x[i][4] * y[4][j]) % MOD;
            }
        }
        return res;
    }
}

552. 学生出勤记录 II（🚹递归公式 & 矩阵快速幂优化🐂）

https://leetcode.cn/problems/student-attendance-record-ii/

提示：
1 <= n <= 10^5

解法1——动态规划

class Solution {
    final int MOD = (int)1e9 + 7;

    public int checkRecord(int n) {
        // 长度，A 的数量，结尾连续 L 的数量
        int[][][] dp = new int[n + 1][2][3];    
        dp[0][0][0] = 1;
        for (int i = 1; i <= n; ++i) {
            // 以P结尾
            for (int j = 0; j < 2; ++j) {
                for (int k = 0; k < 3; ++k) {
                    dp[i][j][0] = (dp[i][j][0] + dp[i - 1][j][k]) % MOD;
                }
            }
            // 以A结尾
            for (int k = 0; k < 3; ++k) {
                dp[i][1][0] = (dp[i][1][0] + dp[i - 1][0][k]) % MOD;
            }
            // 以L结尾
            for (int j = 0; j < 2; ++j) {
                for (int k = 1; k < 3; ++k) {
                    dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k - 1]) % MOD;
                }
            }
        }

        int ans = 0;
        for (int j = 0; j < 2; ++j) {
            for (int k = 0; k < 3; ++k) {
                ans = (ans + dp[n][j][k]) % MOD;
            }
        }
        return ans;
    }
}

解法2——矩阵快速幂优化DP（TODO）

在这里插入代码片

790. 多米诺和托米诺平铺⭐（🚹想出递推公式）

https://leetcode.cn/problems/domino-and-tromino-tiling/

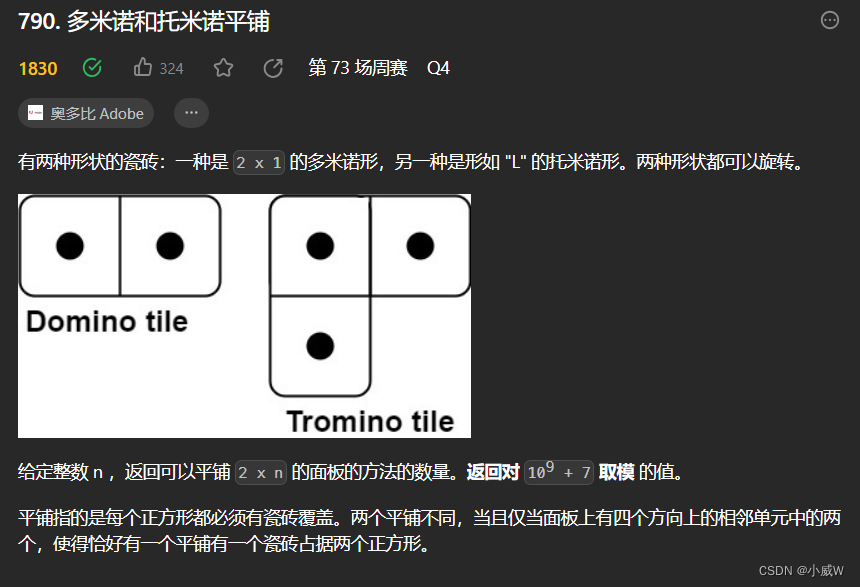
提示：
1 <= n <= 1000

解法1——动态规划1 分最后一列的状态

https://leetcode.cn/problems/domino-and-tromino-tiling/solutions/1962465/duo-mi-nuo-he-tuo-mi-nuo-ping-pu-by-leet-7n0j/

class Solution {
    final int MOD = (int)1e9 + 7;

    public int numTilings(int n) {
        // 0空，1上，2下，3满
        int[][] dp = new int[n][4];
        dp[0][0] = dp[0][3] = 1;
        for (int i = 1; i < n; ++i) {
            dp[i][0] = dp[i - 1][3];
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % MOD;
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % MOD;
            dp[i][3] = (((dp[i - 1][0] + dp[i - 1][1]) % MOD + dp[i - 1][2]) % MOD + dp[i - 1][3]) % MOD;
        }
        return dp[n - 1][3];
    }
}

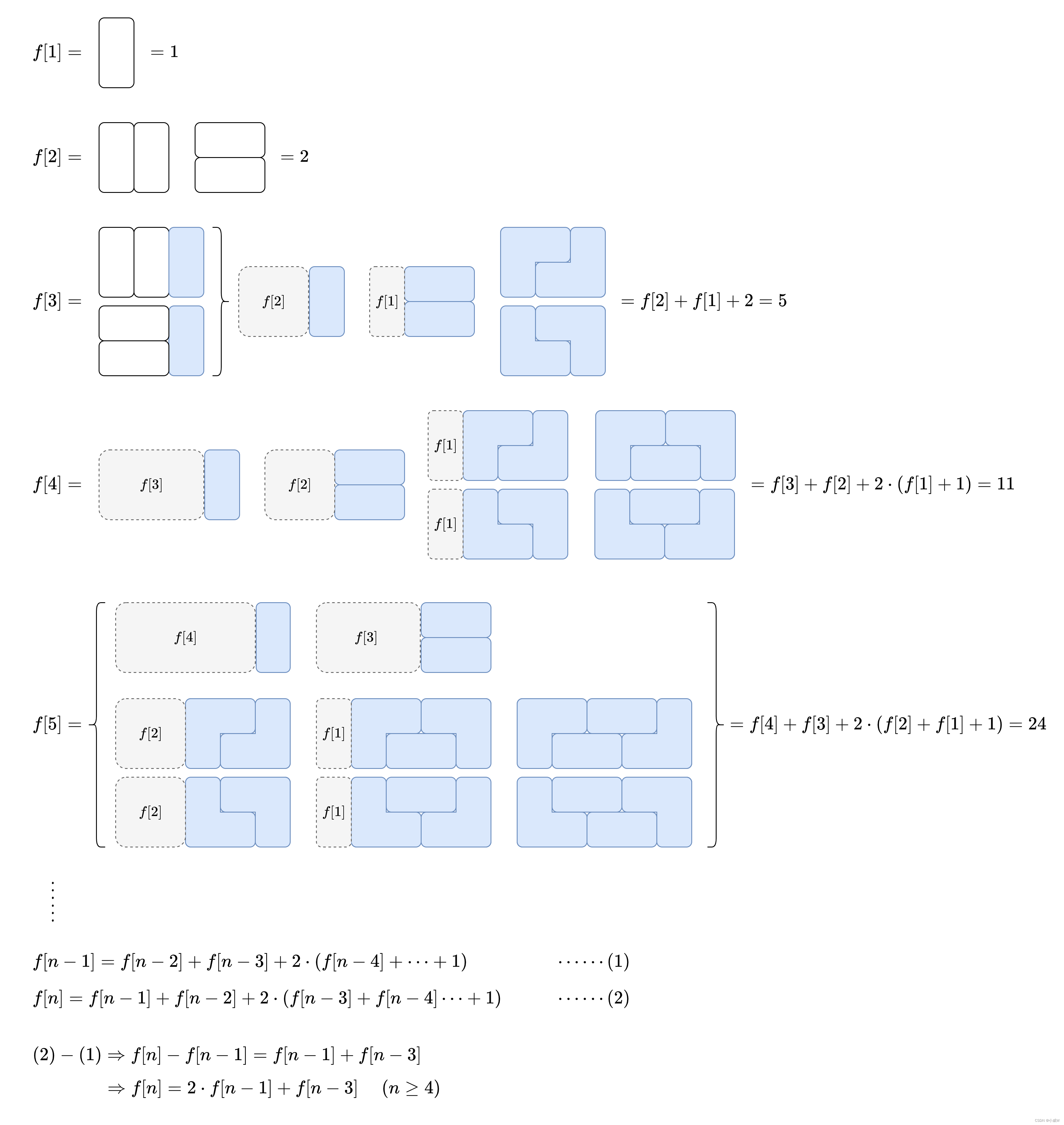
解法2——动态规划2 列出式子找通项公式（TODO 还没想明白）

https://leetcode.cn/problems/domino-and-tromino-tiling/solutions/1968516/by-endlesscheng-umpp/

class Solution {
    final long MOD = (long)1e9 + 7;

    public int numTilings(int n) {
        if (n <= 2) return n;
        long[] dp = new long[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; ++i) {
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % MOD;
        }
        return (int)dp[n];
    }
}

解法3——矩阵快速幂优化DP

class Solution {
    final int MOD = (int)1e9 + 7;

    public int numTilings(int n) {
        // 0空，1上，2下，3满
        long[][] m = {
            {0, 0, 0, 1},
            {1, 0, 1, 0},
            {1, 1, 0, 0},
            {1, 1, 1, 1}
        };
        return (int)pow(m, n - 1)[3][0];
    }

    public long[][] pow(long[][] m, int k) {
        long[][] res = {
            {1, 0, 0, 0},
            {0, 0, 0, 0},
            {0, 0, 0, 0},
            {1, 0, 0, 0}
        };
        for (; k != 0; k >>= 1) {
            if ((k & 1) == 1) res = mul(m, res);
            m = mul(m, m);
        }
        return res;
    }

    public long[][] mul(long[][] a, long[][] b) {
        long[][] c = new long[4][4];
        for (int i = 0; i < 4; ++i) {
            for (int j = 0; j < 4; ++j) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j] + a[i][2] * b[2][j] + a[i][3] * b[3][j]) % MOD;
            }
        }
        return c;
    }
}

成绩记录

本次没有参加竞赛。