5. 支持向量机(线性SVM)

5.4 非线性可分SVM

5.4.1 非线性可分问题

原始空间不存在能够正确划分的超平面

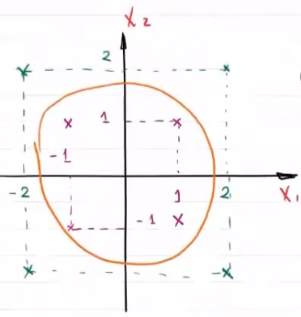
在二维平面直角坐标系中，如果按照与原点之间的距离对数据点进行分类的话，分类模型就成为一个圆，也就是超平面

处理思路

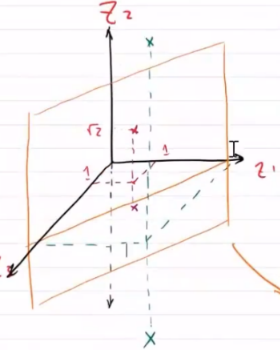
如果能将样本从原始空间映射到高维特征空间上，在新的特征空间是上样本就可能是线性可分的

• 若样本的属性数优先，则一定存在一个高维特征空间使样本可分

核技巧

通过一个非线性映射，将原始低维空间上的非线性问题转化为新的高维空间上的线性问题，这就是核技巧的基本思想。

使在原始空间 $R^n$ 中的超平面模型映射为特征空间的超平面模型

在学习和预测中，只定义核函数，而不显式定义映射函数，利用线性分类方法与核函数解决非线性问题

核函数

假设原始空间是 低维欧几里得空间 $\mathcal{X}$ ，新空间为 **高维希尔伯特空间 $\mathcal{H}$ ** ，从 $\mathcal{X}$ 到 $\mathcal{H}$ 的映射可以用函数 $\varphi (x):\mathcal{X}\to \mathcal{H}$ 表示。核函数可以表示为映射函数内积形式
$$K(x,z)=\varphi (x)\cdot \varphi (z)$$

eg

原空间 $\mathcal{X}$ 中的两个点进行内积运算 $(x_i,x_j)$ ，若先进行映射再在 $\mathcal{H}$ 中内积运算，则有
$$z_i=\varphi (x_i),z_j=\varphi (x_j),则(z_i,z_j)=\varphi (x_i)\cdot \varphi (x_j)$$
若使用核函数，则可直接计算 $K(x_i,x_j)$

特点

对于确定的核函数

1. 计算过程在低维空间上完成，避免了高维空间中的复杂计算

2. 对于给定核函数，高维空间 $\mathcal{H}$ 和映射函数 $\varphi$ 的取法不唯一

   可映射到不同的特征空间，$z_i$ 维度可以不同和

   可通过不同映射函数，映射到同一特征空间

核函数作用于SVM

输入：线性不可分的数据
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } ∈ X ∈ R n , y i ∈ Y ∈ { + 1 , − 1 } , i = 1 , ⋯   , N D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}\in \mathcal{X}\in R^n,y_i\in \mathcal{Y}\in \{+1,-1\},i=1,\cdots,N D={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}∈X∈Rn,yi​∈Y∈{+1,−1},i=1,⋯,N
输出：分离超平面和决策函数

算法：

1. 选择合适的参数 $C$ 和核函数 $K(x,z)$ ，构造最优化问题

线性SVM
$$\{\begin{array}{l}\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i\cdot x_j-\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$
对于 $(x_i,x_j)$ ，可以通过核技巧映射到线性可分空间
$$\varphi (x_i)\cdot \varphi (x_j)=z_i\cdot z_j=K(x_i,x_j)$$
在 $\mathcal{H}$ 空间中的SVM问题为
$$\{\begin{array}{l}\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ s.t.0\le {\alpha }_i\le 0\\ \sum _{i=1}^N{\alpha }_i{y}_i=0\end{array}$$
求得最优解 ${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast })$

2. 选一个 $0<{\alpha }_j^{\ast }<C$ 的分量对应的样本点 $(x_j,y_j)$ ——支持向量，计算模型参数 ${\omega }^{\ast },b^{\ast }$

有 ${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(\cdot ,x_i)$ ， $b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)$

模型
$$\{\begin{array}{l}\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x)+\left(y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)\right)=0\\ 决策函数f(x)=sign\left[\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x)+\left(y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)\right)\right]\end{array}$$
所以问题的关键为 如何确定核函数 $K(x_i,x_j)$

5.4.2 正定核函数

对于内积运算，
$$\begin{array}{rl}(x,x)>0，当x>0时& ——正定性\\ (x_i,x_j)=(x_j,x_i)& ——非负性\end{array}\}\Rightarrow 正定核$$
故正定核函数应满足：

1. 对称性： $K(x,z)=K(z,x)$

2. 正定性：$\forall x_1,x_2\cdots ,x_N\in R^n$ ，$K(x_i,x_j)$ 的Gram阵是半正定的

   • Gram阵
     $$原\left[\begin{array}{ccc}(x_1,x_1)& \cdots & (x_1,x_N)\\ ⋮& \ddots & ⋮\\ (x_N,x_1)& \cdots & (x_N,x_N)\end{array}\right]新\left[\begin{array}{ccc}K(x_1,x_1)& \cdots & K(x_1,x_N)\\ ⋮& \ddots & ⋮\\ K(x_N,x_1)& \cdots & K(x_N,x_N)\end{array}\right]$$

   • 半正定

     对于A，$\forall x\ne 0$ ，有$x^{T}Ax\ge 0$ ，则有A为半正定阵

     半正定判定 $\{\begin{array}{l}{x}^{T}Ax=y^{T}Dy——D为对角阵\\ 全部特根\lambda \ge 0\\ 所有主子行列式\ge 0\end{array}$

由$K(x,z)$ 构造 $\mathcal{H}$ 空间

任何一个核函数都隐式定义了一个成为 再生核希尔伯特空间 的特征空间
欧式空间 { 空间 ( 集合 ) → 元素是向量 向量空间 ⊆ 线性空间 ( 元素 + 数乘 ∈ 空间 ) → 内积 内积空间 { 表示向量间关系 用夹角表示，用 ( a , b ) 度量夹角大小 → 范数 赋范线性空间——表示向量大小、长度 数列存在极限且 ∈ 空间，任一柯西列都是收敛列 { x 1 ⋯   , x N } { x 1 > x 2 > ⋯ > x N 且 x 1 − x 2 > x 2 − x 3 > ⋯ > x N − 1 − x N ( 柯西列 ) → 0   ↓ 巴拿赫空间 \begin{aligned} &欧式空间&\begin{cases} 空间(集合)\xrightarrow{元素是向量}向量空间\subseteq 线性空间(元素+数乘\in 空间)\\ \xrightarrow{内积}内积空间\begin{cases} 表示向量间关系\\ 用夹角表示，用(a,b)度量夹角大小 \end{cases}\\ \xrightarrow{范数}赋范线性空间——表示向量大小、长度 \end{cases}\\ &&数列存在极限且\in 空间，任一柯西列都是收敛列\{x_1\cdots,x_N\}\\ &&\begin{cases} x_1>x_2>\cdots>x_N\\ 且x_1-x_2>x_2-x_3>\cdots>x_{N-1}-x_N(柯西列)\rightarrow 0\ \end{cases}\\ &\downarrow\\ &巴拿赫空间 \end{aligned} ​欧式空间↓巴拿赫空间​⎩ ⎨ ⎧​空间(集合)元素是向量 ​向量空间⊆线性空间(元素+数乘∈空间)内积 ​内积空间{表示向量间关系用夹角表示，用(a,b)度量夹角大小​范数 ​赋范线性空间——表示向量大小、长度​数列存在极限且∈空间，任一柯西列都是收敛列{x1​⋯,xN​}{x1​>x2​>⋯>xN​且x1​−x2​>x2​−x3​>⋯>xN−1​−xN​(柯西列)→0 ​​
对于非欧氏空间上的完备空间，称为希尔伯特空间 $\mathcal{H}$

步骤

1. 定义映射

$\varphi :x\to K(\cdot ,x)$

• $\cdot$ 表示任一位置元素
• $\varphi (\cdot )\cdot \varphi (x)=K(\cdot ,x)$ 表示 $\varphi (x)$ 与任一个元素的内积为 $K(\cdot ,x)$

表示这个映射受核函数约束

线性组合： $f(\cdot )=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)$ ——向量
S = { f ( ⋅ ) } ——向量空间 S=\{f(\cdot)\}——向量空间 S={f(⋅)}——向量空间
2. $S\stackrel{+内积}{\to }内积空间$
$$\begin{array}{r}f(\cdot )=\sum _{i=1}^m{\alpha }_{i}K(\cdot ,x_i)\\ g(\cdot )=\sum _{j=1}^l{\beta }_j(\cdot ,z_j)\end{array}\}\Rightarrow f\cdot g=\sum _{i=1}^m\sum _{j=1}^l{\alpha }_i{\beta }_{j}K(x_i,z_j)$$
证明：
$$\begin{array}{rl}& f\cdot f\ge 0\\ & f\cdot f=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)\ge 0\\ & 令x=({\alpha }_1,\cdots ,{\alpha }_m{)}^T,G=\left[\begin{array}{ccc}K(x_1,x_1)& \cdots & K(x_1,x_m)\\ ⋮& \ddots & ⋮\\ K(x_m,x_1)& \cdots & K(x_m,x_m)\end{array}\right]\\ & \begin{array}{rl}{x}^{T}Gx& =({\alpha }_1,\cdots ,{\alpha }_m)G({\alpha }_1,\cdots ,{\alpha }_m{)}^T\\ & =\left[\begin{array}{c}{\alpha }_{1}K(x_1,x_1)+{\alpha }_{2}K(x_2,x_1)+\cdots +{\alpha }_{m}K(x_m,x_1)\\ ⋮\\ {\alpha }_{1}K(x_1,x_m)+{\alpha }_{2}K(x_2,x_m)+\cdots +{\alpha }_{m}K(x_m,x_m)\end{array}\right]({\alpha }_1,\cdots ,{\alpha }_m{)}^T\\ & =\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_{j}K(x_i,x_j)\ge 0\end{array}\end{array}$$
3. $S\stackrel{+范数}{\to }赋范空间\stackrel{完备化}{\to }\mathcal{H}$

再生性
$$\begin{gathered} K(\cdot ,x)\cdot K(\cdot ,z)=K(x,z) \\ f(\cdot )=\sum _i{\alpha }_{i}K(\cdot ,x_i) \\ K(\cdot ,x)f(\cdot )=\sum _i{\alpha }_{i}K(x,x_i)=f(x) \end{gathered}$$

常用核函数

在支持向量机中，核函数的选择是一个核心问题，常用核函数有：

线性核 ：$K(X,Y)=X^{T}Y$

多项式核 ：$K(X,Y)=(X^{T}Y+c{)}^d$ ，$c$ 为常数，$d\ge 1$ 为多项式次数

高斯核 ：$K(X,Y)=e^{-\frac{\Vert X-Y{\Vert }^2}{2{\sigma }^2}}$ ，$\sigma >0$ 为高斯核带宽

拉普拉斯核 ：$K(X,Y)=e^{-\frac{\Vert X-Y\Vert }{\sigma }}$

sigmod核 ：$K(X,Y)=tanh(\beta X^{T}Y+\theta )$ ，$\beta >0$ ，$\theta <0$

5.5 SVM参数求解算法

将支持向量机的最优化作为原始问题，应用最优化理论中的拉格朗日对偶性，可以通过求解其对偶问题得到原始问题的最优解

SVM关键是如何根据支持向量构建解，算法的复杂度也主要取决于支持向量的数目

在算法实现过程中，支持向量机会遇到大量训练样本下，全局最优解难以求得的情况——SMO算法（序列最小最优化）

支持向量机的学习问题可以形式化为凸二次规划问题的求解，SMO算法的特点是不断将原始的二次规划问题分解为只有两个变量的二次规划子问题，并求解子问题的解析解，直到所有变量满足条件为止

5.6 SVM与线性模型关系

逻辑斯蒂模型损失函数
$$\begin{array}{rl}J(\omega )& =-\frac{1}{n}\left[\sum _{i=1}^n\sum _{k=1}^{2}I(y_i=k)\ln P(y_i=k|x_i,\omega )\right]\\ & =-\frac{1}{n}\left[\sum _{i=1}^n{y}_i\ln P(y_i=1|x_i,\omega )+(1-y_i)\ln P(y_i=0|x_i,\omega )\right]\end{array}$$
正则化
$$J(\omega )+\frac{\lambda }{2n}\Vert \omega {\Vert }_2^2$$
即逻辑斯蒂模型先有损失函数，再做正则化

---

SVM：将损失函数作为约束，先求出参数，再以损失函数为约束